Рассеяние свободных электронов на точечных дефектах кристаллической решётки

1. Введение

С целью повышения прочностных свойств металлических материалов их подвергают интенсивной пластической деформации (ИПД), что позволяет вводить в структуру материала различные дефекты кристаллической решетки. Их влияние на механическую прочность полученных таким образом ультрамелкозернистых материалов достаточно хорошо изучена. Для возможности анализа влияния структурных дефектов на физические свойства и прогноза их изменения в зависимости от факторов, к которым они являются чувствительными, необходимы соответствующие аналитические зависимости между ними. В частности, востребованными являются материалы, обладающие высокой прочностью и достаточной электропроводностью. Целью данной работы явилось вычисление усредненной вероятности рассеяния в единицу времени электронов на вакансиях и примесных атомах, которое позволяет определить время релаксации и соответственно вклад в удельное сопротивление указанных точечных дефектов. Сравнение полученных результатов с известными экспериментальными данными и получение уточненных размеров области взаимодействия электрона с вакансиями и примесными атомами позволяет повысит точность оценок.

2. Удельное сопротивление и прочность металлов, содержащих вакансии

Вклад в удельное сопротивление металлов дефектов кристаллической решетки зависит от вероятности P рассеяния электронов на них, которая определяется размерами области рассеяния. Для вычисления величины P необходимо задать вид рассеивающего потенциала.

Рассмотрим систему из N_e электронов — невзаимодействующих фермионов со спином ½, заключенных в объеме Ω при температуре T=0. Решения уравнения Шредингера для свободной частицы имеют вид плоских волн: ψ_k=exp(), — радиус-вектор. При этом в k — пространстве волновых чисел на каждое состояние приходится объем dV_k=(2π)³/L³=(2π)³/Ω.

Плотность квантовых состояний в металле (плотность разрешенных состояний электронов в единичном интервале энергии E) равна

.(1)

На уровне Ферми , где n_e — объемная плотность электронов, E_F — энергия Ферми. Потенциал вакантной области U определим плотностью электронов в материале, деленной на плотность состояний: U=(2/3)E_F [1]. Чтобы вычислить время релаксации τ_k, необходимо знать вероятность P того, что электрон в единицу времени испытает столкновение с вакансией: τ_k~1/P. Рассеиваются лишь электроны в окрестности энергии Ферми. Вычислим вероятность перехода электрона из состояния с волновым числом k в состояние k′ в k — пространстве. Вероятность рассеяния в телесный угол dw в единицу времени равна

,(2)

где — матричный элемент рассеяния (перехода из состояния k в состояние k′ в k — пространстве, ):

Возмущение оператора Гамильтона примем равным потенциалу вакантной областиU. При рассеянии энергия частицы сохраняется: . Соответственно стационарное решение уравнения Шредингера запишем в виде . Область рассеяния электронов τ вакансией представим в виде куба, одна из граней которого параллельна вектору . Объем куба равен l³.

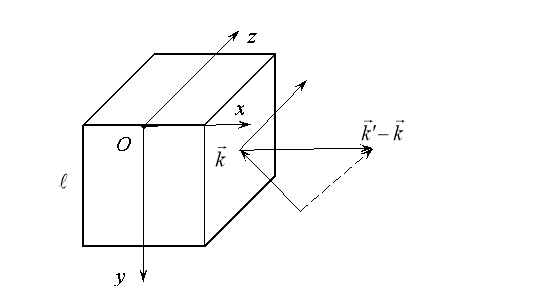
Модуль вектора равен. Тогда вероятность рассеяния (2) примет вид

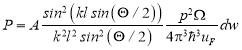,(4)

где .

Усредненная вероятность рассеяния в единицу времени по всем направлениям вектора в образце с N_=C_Ω=C_an_a вакансиями, где n_a — плотность атомов, C_ и C_a — объемная и атомная концентрации вакансий соответственно, равна

.(5)

Тогда вклад в удельное сопротивление вакансий определится выражением:

.(6)

Согласно известным теоретическим оценкам [2–5] вклад в удельное сопротивление благородных металлов для одного процента вакансий равен ρ_V=1.5 мкОм∙см, что совпадает с экспериментальными значениями. Известны также значения, полученные рядом авторов для меди, равные 1.64 [6], 1.70 [7] и 1.73 мкОм∙см/at. % [8]. Вклад вакансий в удельное сопротивление меди, согласно формуле (6) равен мкОм∙м, или 1.0 мкОм∙см/at. %, если принять объем области взаимодействия равным l³=a³/4, где а — параметр решетки. Полученная оценка ниже известных теоретических оценок. Результат, полученный в данной работе с использованием потенциала U [1], зависит от размера области взаимодействия l и соответствует известным данным по порядку величины. Если принять значение l равным длине вектора Бюргерса b, то прирост удельного сопротивления составит 1.42 мкОм∙см/at. %. При l=1.06b мкОм∙см/at. %. Если принять l1.06b, то прирост удельного сопротивления при концентрации вакансий C_Va=10–⁵, характерной для материалов, подвергнутых ИПД, составит 1.73∙10–³ мкОм∙см. В то же время удельное сопротивления чистой меди при комнатной температуре равно мкОм∙см [9]. Таким образом, вклад вакансий в удельное сопротивление весьма незначителен.

Удельное сопротивление, обусловленное рассеянием электронов на легирующих атомах, может быть вычислено и по формуле (6), полученной для случая рассеяния на вакансиях. В данном случае вместо атомной концентрации вакансий C_a нужно брать атомную концентрацию атомов C_a. Результаты вычислений приводят к значению мкОм∙см при l=1.35b и C_a=6.1∙10^–3 (ρ_a=5.15 мкОм∙см/at. %).

Согласно экспериментальным данным, электропроводимость сплава Сu-0.5wt. %Cr, подвергнутого 4 проходам равноканального углового прессования, равно 35 % IACS (=4.93∙10^–8 Ом∙м) [10]. Характерное значение плотности дислокаций составляет ρ_tot= 8.33∙10¹⁴ m^-2, вклад которых в удельное сопротивление сплава равен ρ_disl.=1.42∙10^–10 Ом∙м. С учетом вклада вакансий, концентрация которых может достигать значений порядка 10–⁵, ρ_=1.73∙10^–3 мкОм∙см и удельного сопротивления чистой меди, равного мкОм∙см можно определить удельное сопротивление, обусловленное легирующими атомами хрома: _a=-₀-_V-_disl.=3.19 ∙10^–8 Ом∙м. Полученное значение может быть использовано для определения размеров области взаимодействия атомов с электронами. В данном случае l_a1.354b.

4. Выводы

Результаты, полученные по представленным в работе формулам, согласуются с экспериментальными данными по порядку величины. По известным экспериментальным данным могут быть уточнены размеры области взаимодействия электронов с дефектами кристаллической решетки, что позволяет повысить точность оценок. Область рассеяния вакансий имеет размеры l1.06b. Размер области взаимодействия для атомов составляет l1.35b. Как следует из проведенных расчетов удельное сопротивление сплава Сu-0.5wt. %Cr существенно повышают растворенные в матрице атомы хрома. Наличие вакансий и дислокаций не оказывает какого-либо заметного влияния на электропроводимость материала.

Литература:

1. Harrison W A 1958 J. Phys. Chem. Solids 5 44
2. Blatt F J 1956 Phys. Rev. 103 1905
3. Abeles M F 1953 Compt. Rend. Acad. Sci. 237 796
4. Seeger A, Stehle H 1956 Z. Phys. 146 242
5. Blatt F J 1957 Solid State Physics 3
6. Seeger A 1962 J. Phys. Rad. 146 242
7. Polác J 1967 Czech. J. Phys. B17 171
8. Fischer K 1963 Phys. Stat. Solidi 3 2035
9. Осинцев О Е 2004 Медь и медные сплавы (Машиностроение) p 336
10. Wei K X, Wei W., Wang F, Du Q B, Alexandrov I V., Hu J 2011 Materials Science and Engineering A528 Issue 3 1478