Энергоэффективность характеризует устойчивым постоянным ростом стоимости электрической энергии, необходимостью уменьшения потерь электроэнергии в процессе ее производства и доставки до потребителей. Существующие способы экономии электроэнергии не могут обеспечивать достижения максимально возможных энергетических показателей. Необходимо разработать новые способы и подходы к проблеме снижения потерь электроэнергии.
- Использование методики оценки статистических характеристик изаконов распределения вероятности энергетических параметров врасчете зависимости электропотребления от объемов горных работ
Общие черты статистического метода в различных областях знания сводятся к подсчету числа объектов, входящих в те или иные группы, рассмотрению распределения количественных признаков, применению выборочного метода, когда детальное исследование всех объектов обширной совокупности, например совокупности многоделимой массы горных пород или потребление электроэнергии на объема массы полезного ископаемого затруднительно. Теория вероятности используется также при оценке достаточности числа наблюдений для тех или иных выводов.
Нахождение статистических характеристик:
Исходные данные
Таблица 1
Потребляемая электроэнергия, объем горной массы, переработанной экскаватором, иудельный расход электроэнергии экскаватора. Шахта северная, февраль, смена 2
|
№п/п |
Объем горной массы, переработанной экскаватором Q, тыс. м3 |
Потребляемая электроэнергия W, кВт. ч |
Удельная норма расхода, |
|
1 |
1158 |
4498,03 |
3,884309 |
|
2 |
1747 |
2786,13 |
1,594808 |
|
3 |
1996 |
2573,57 |
1,289364 |
|
4 |
1968 |
3142,68 |
1,59689 |
|
5 |
1219 |
3707,22 |
3,041198 |
|
6 |
1126 |
3010,12 |
2,673286 |
|
7 |
1375 |
4534,6 |
3,297891 |
|
8 |
1622 |
3442,09 |
2,122127 |
|
9 |
1317 |
3956,35 |
3,004062 |
|
10 |
1984 |
2779,27 |
1,400842 |
|
11 |
1506 |
2740,42 |
1,819668 |
|
12 |
1731 |
4534,6 |
2,619642 |
|
13 |
1216 |
4280,9 |
3,520477 |
|
14 |
1199 |
3083,25 |
2,571518 |
|
15 |
1984 |
3778,07 |
1,904269 |
|
16 |
1873 |
4445,46 |
2,373444 |
|
17 |
1349 |
2719,85 |
2,016197 |
|
18 |
1653 |
2596,43 |
1,570738 |
|
19 |
1945 |
3181,53 |
1,635748 |
|
20 |
1190 |
3604,37 |
3,028882 |
|
21 |
1136 |
4562,03 |
4,015871 |
|
22 |
1392 |
3451,23 |
2,479332 |
|
23 |
1577 |
3716,36 |
2,356601 |
|
24 |
1996 |
4038,63 |
2,023362 |
|
25 |
1510 |
4166,62 |
2,759351 |
|
26 |
1626 |
2962,12 |
1,821722 |
|
27 |
1767 |
3405,52 |
1,927289 |
|
28 |
1823 |
3256,96 |
3,884309 |
Общей характеристикой вариационного ряда служит средняя величина:
h=![]() , (1)
, (1)
3. Вычисляем медиану:
Медиана- значение признака, соответствующего середине упорядоченного вариационного ряда.
При постоянстве плотности внутри интервалов (классов) значение медианы определяют по формуле:
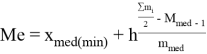 ; (2)
; (2)
где ![]() - нижняя граница медианного ряда; h- интервальная разность; М — накопленная частота интервала, предшествующего медианному;
- нижняя граница медианного ряда; h- интервальная разность; М — накопленная частота интервала, предшествующего медианному; ![]() - частота медианного интервала.
- частота медианного интервала.
4. Вычисляем моду
В интервальном ряду интервал, содержащий моду, определяют по наибольшей частоте (когда интервалы равны) или по наибольшей плотности (когда интервалы не равны). Вычисляем по формуле:
![]() (3)
(3)
где ![]() — нижняя граница модального интервала;
— нижняя граница модального интервала;
mmod — частота модального интервала.
5. Находим дисперсию![]() (средний квадрат отклонения)
(средний квадрат отклонения)
Является наиболее распространенной характеристикой степени колеблемости признака.
Определяется по формуле:
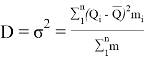 ; (4)
; (4)
Для характеристики степени вариации признака чаще используют относительные показатели — коэффициент вариации, вычисляемое по формуле:
![]() . (5)
. (5)
6. Определяем условные моменты относительно ложного нуля
Условные моменты относительно ложного нуля находят из выражения:
![]() или
или ![]() ; (6)
; (6)
где ![]() .
.
7. Определим центральные моменты
Между центральными и условными моментами следующая связь:
![]() ;
;
![]() ; (7)
; (7)
8. Зная центральные моменты третьего и четвертого порядков, вычисляем асимметрию и эксцесс вариационного ряда.
Мерой асимметрии вариационного ряда служит нормированный момент третьего порядка, определяемый из выражения
![]() ; (8)
; (8)
Сглаженность кривой вариационного ряда характеризуется эксцессом, который определяется по формуле:
![]() ; (9)
; (9)
9. Для установления зависимости между потребляемой электроэнергией и объемом горной массы, переработанной экскаватором, определяется коэффициент парной корреляции ![]() , определим по формуле:
, определим по формуле:
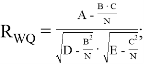 (10)
(10)
10. Чтобы рассчитать значение потребляемой электроэнергии в зависимости от объема горной массы, переработанной экскаватором, найдем коэффициенты уравнения регрессии по формуле:
![]() ; (11)
; (11)
![]() . (12)
. (12)
Определяем статистические характеристики потребляемой электроэнергий W,удельного электропотребления ω и обьема горной массы,переработанной экскаватором Q. Расчеты будем проводить в программе Statistica


Рис. 1. Полученные данные
Определим корреляционные зависимости между ![]() .
.
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
3.1.2.6.Определяем коэффициент парной корреляции:
 (18)
(18)
3.1.2.6. Определяем коэффициенты уравнения регрессии:
![]() ; (19)
; (19)
![]() 4451,951. (20)
4451,951. (20)
Полученное уравнение регрессии позволяет рассчитать значение потребляемой электроэнергии в зависимости от объема горной массы, переработанной экскаватором, графически представлено на рис. 2.
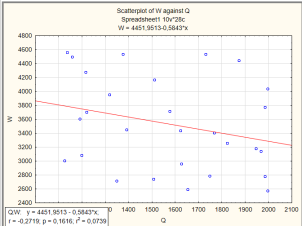
Рис. 2. Зависимость потребляемой электроэнергии ![]() от объема горной массы, переработанной экскаватором
от объема горной массы, переработанной экскаватором ![]()
Для установления зависимости между удельным электропотреблением и объемом горной массы, переработанной экскаватором, определяется коэффициент парной корреляции ![]()
Находим промежуточные коэффициенты: так же как и в формулах (13–17)
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Находим коэффициент парной корреляции (см п.18):

Определяем коэффициенты уравнения регрессии (см п. 19):
![]() -0,00173;
-0,00173;
![]() 5,157544
5,157544![]()
Полученное уравнение регрессии позволяет рассчитать значение потребляемой электроэнергии в зависимости от объема горной массы, переработанной экскаватором, графически представлено на рис. 3.
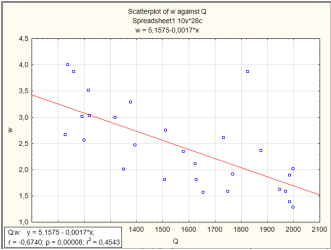
Рис. 3. Зависимость удельного электропотребления ![]() от объема горной массы, переработанной экскаватором
от объема горной массы, переработанной экскаватором ![]()
Таким образом мы можем говорить о электропотреблении, как случайный процесс. Проведя в статистике анализ статистических данных электропотребления на объем добытой горной массы, мы можем прогнозировать с математической точностью потребление электроэнергии в последующие месяцы добычи угольных пород.
Литература:
- Рыжов П. А. Математическая статистика в горном деле. Учебное пособие для вузов спец. «Маркшейдерское дело», М., «Высш. школа», 1973. -287с.
- Левин Б. Р. Статистические основы радиотехники. 3-е изд., перераб. и доп. — М.: Радио и связь, 1989. — 656 с.: ил. — ISBN 5–256–00264–3.







