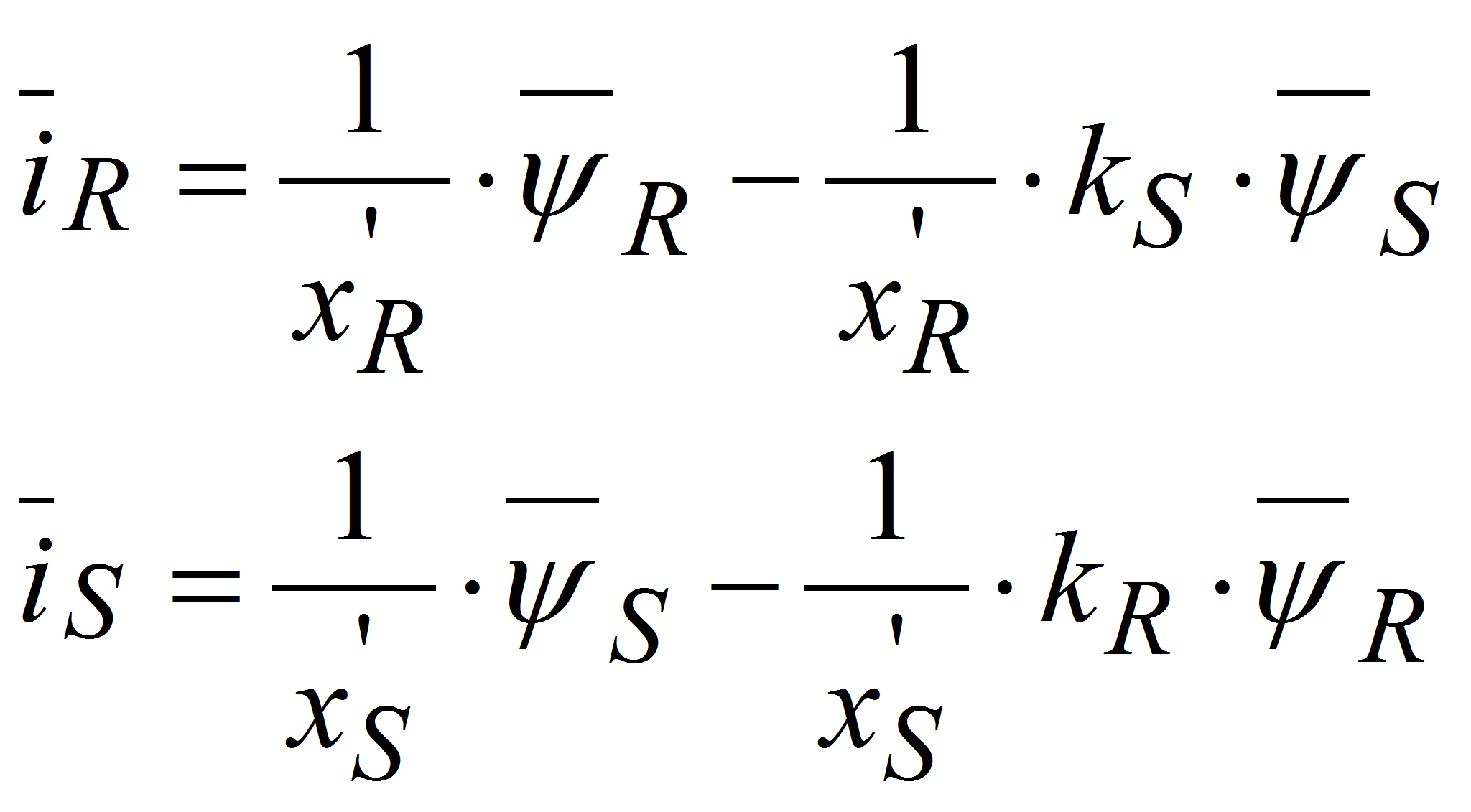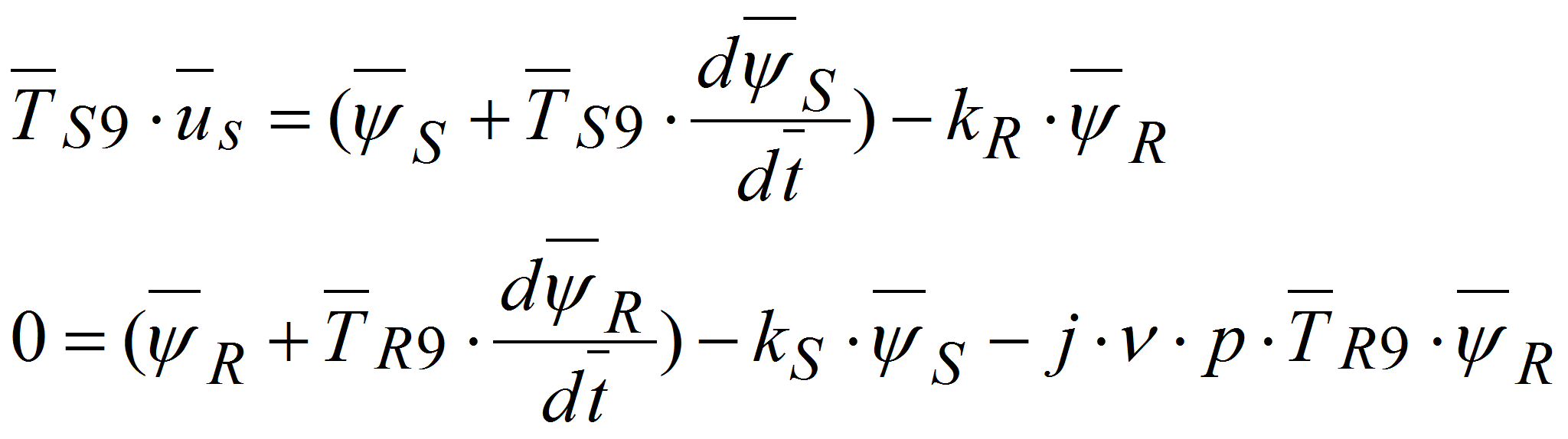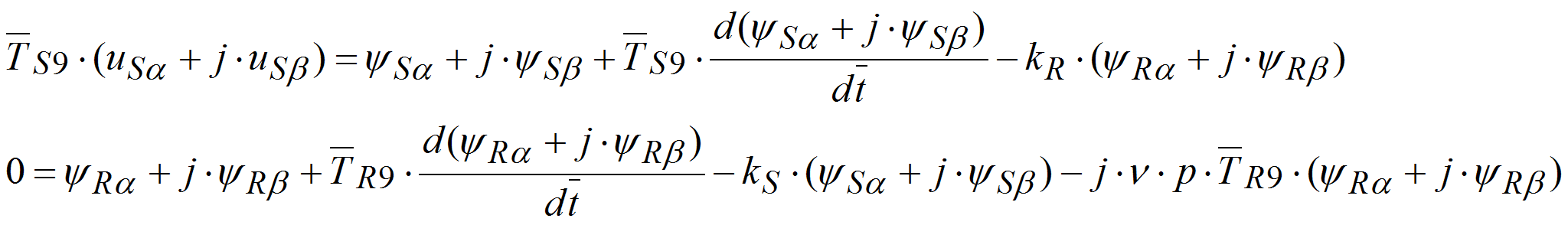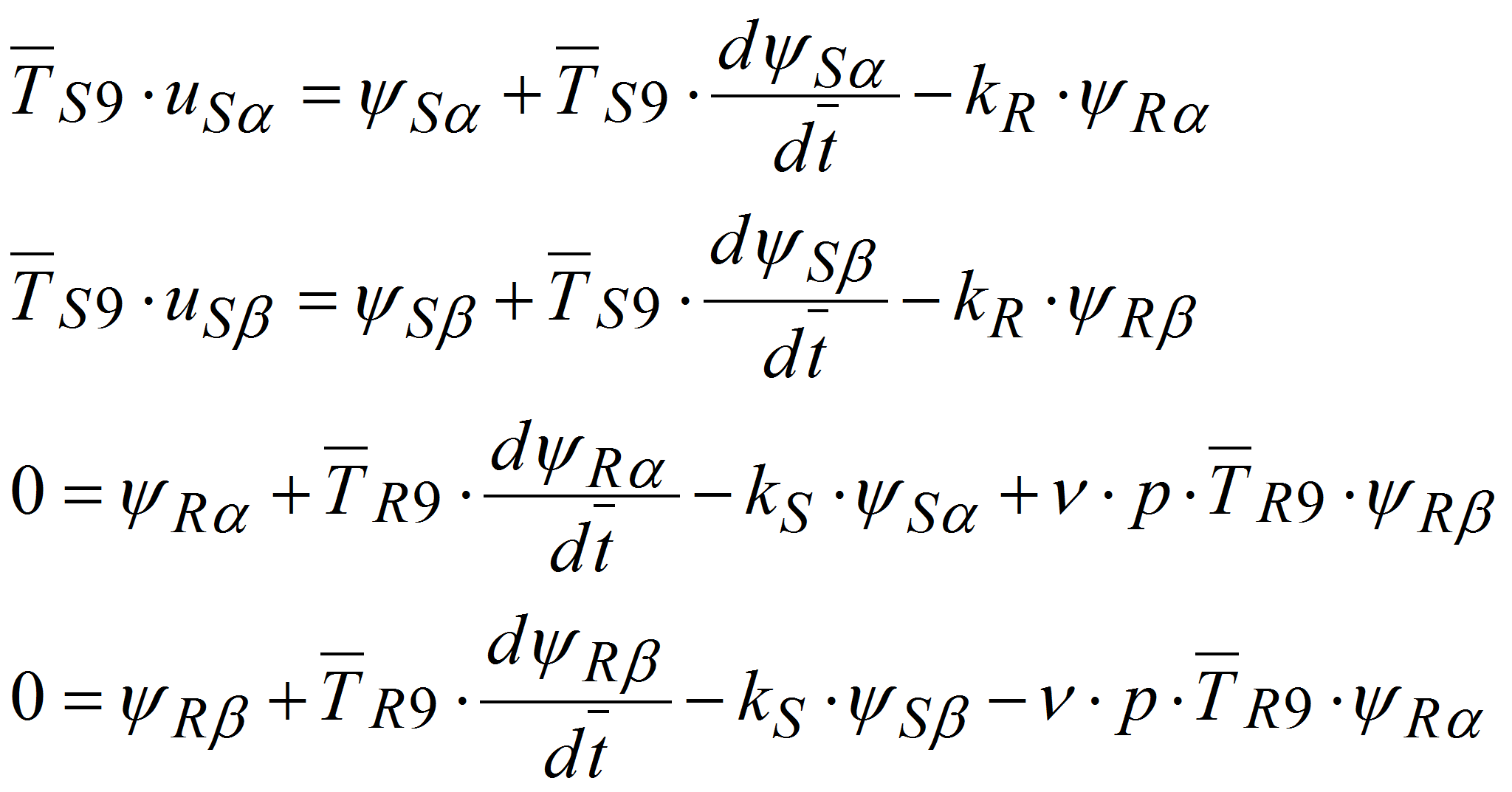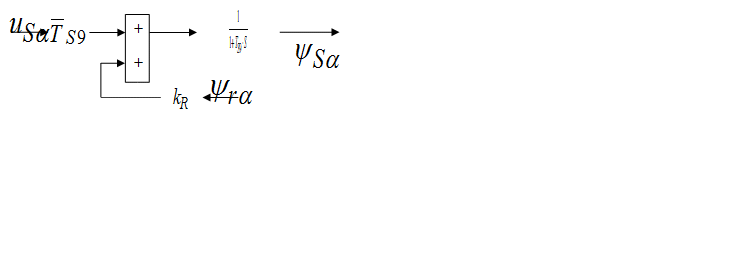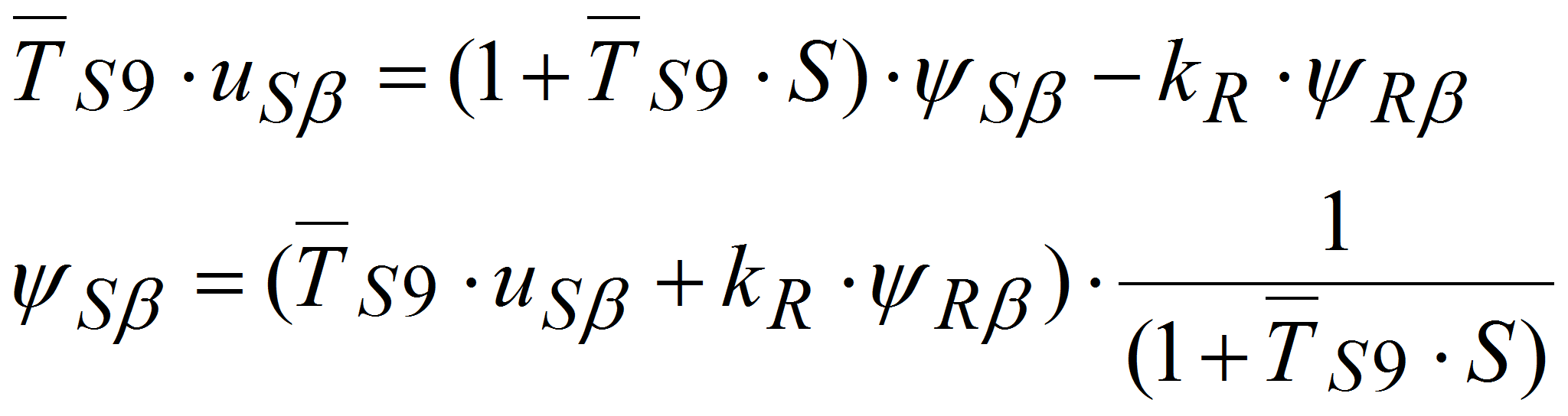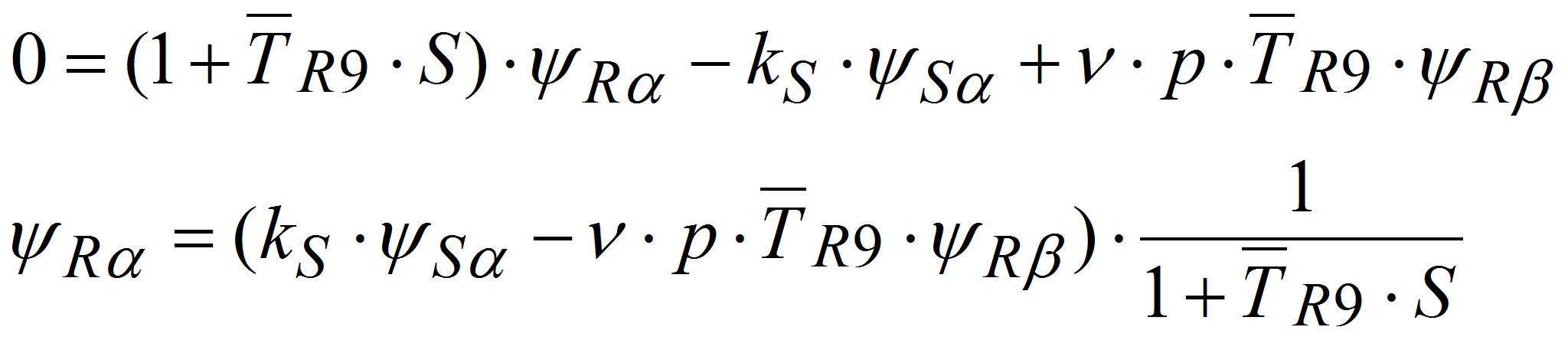Рассмотрим систему уравнений АД с К.З. ротором:
- Определим электромагнитный момент через векторное произведение [1, c. 238]:
- Вычтем второе уравнение из первого:
- Вычтем второе уравнение из первого:
Рассмотрим процессы в неподвижной системе координат,
![]() ,
,
![]() :
:
Вещественную ось обозначим , а мнимую через . Пространственные вектора в этом случае раскладываются по осям:
Подставим эти значения в уравнения и, приравняв отдельно вещественные и мнимые части, получим:
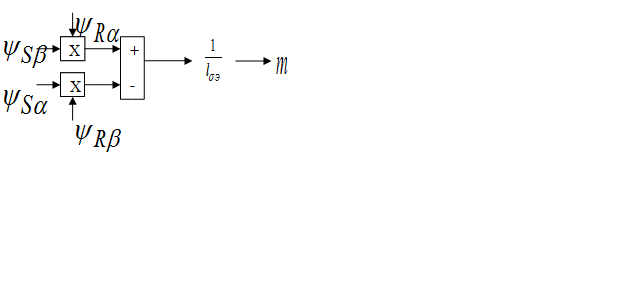
- Окончательно, с учетом электромагнитных моментов систем
уравнений АД в неподвижной системе координат в операторной форме (
 )
запишется в виде:
)
запишется в виде:
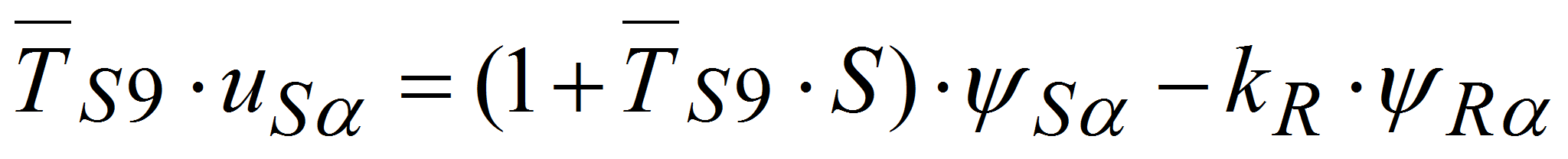 (1)
(1)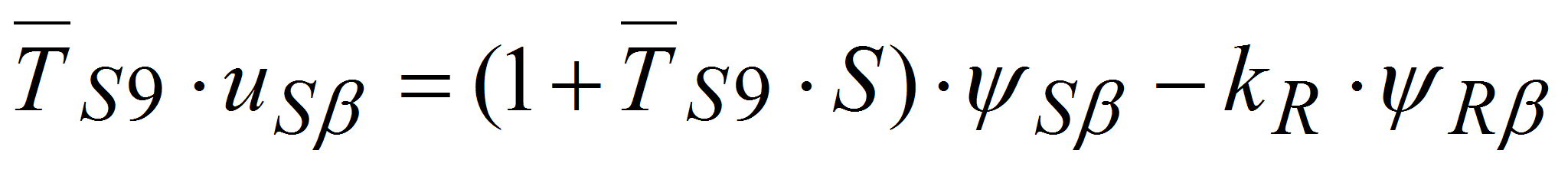 (2)
(2) (3)
(3) (4)
(4)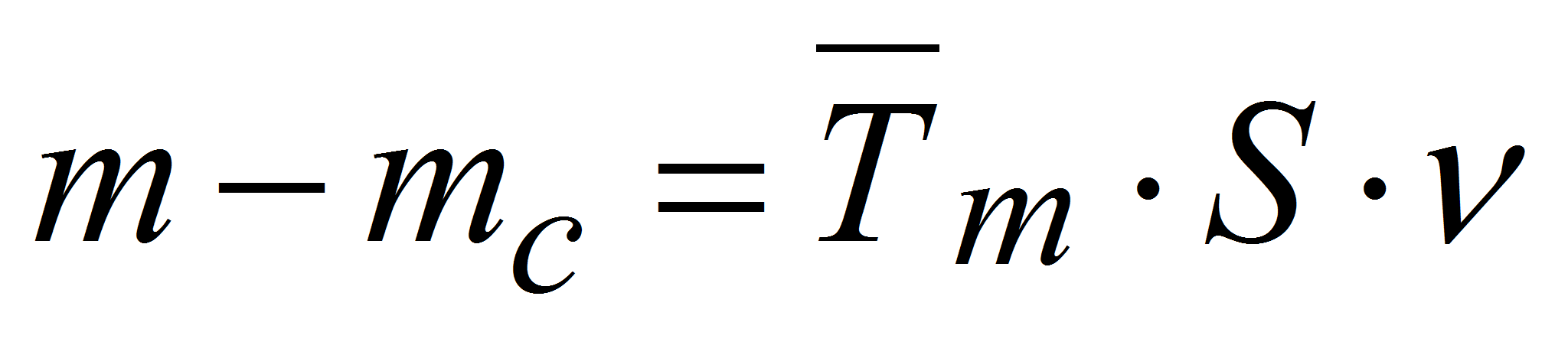 (5)
(5)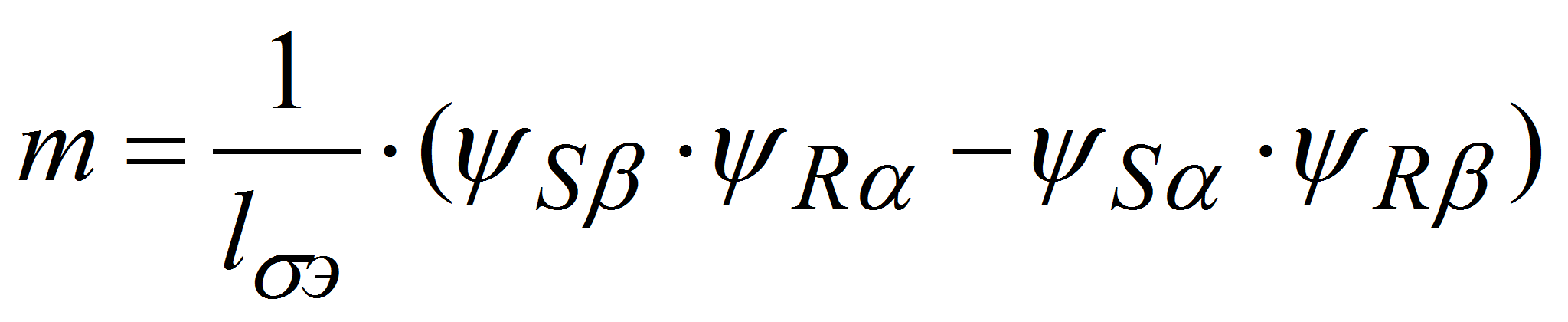 (6)
(6)
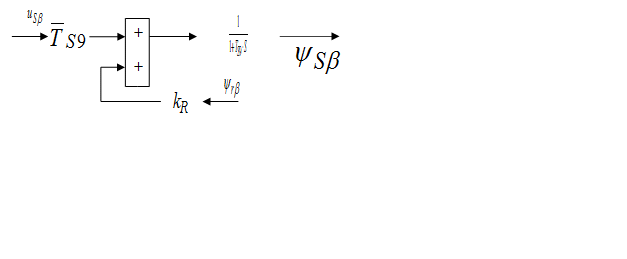
- Структурная схема для уравнения (1):
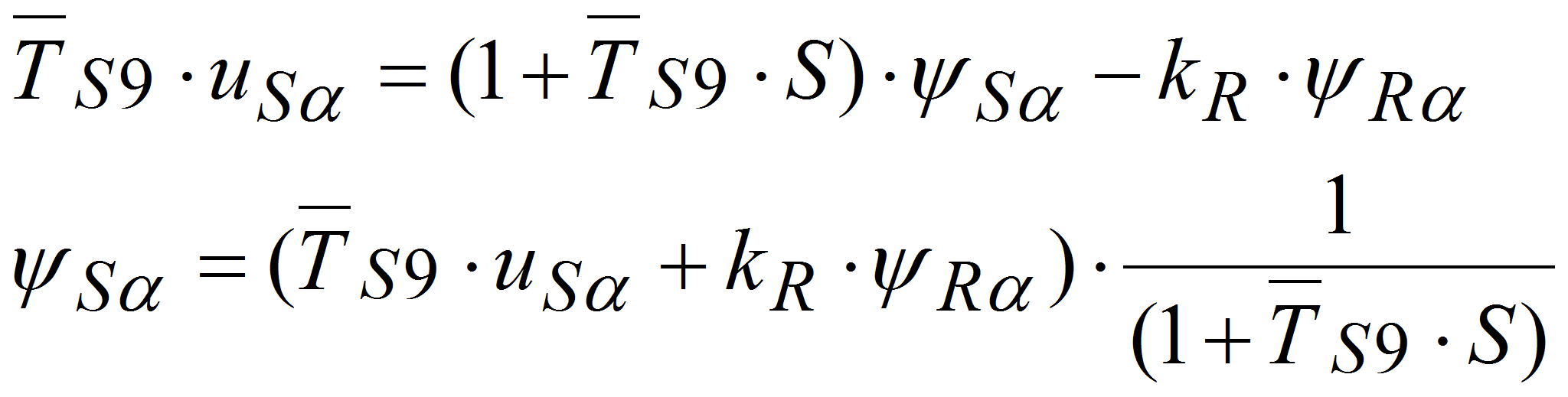
Для моделирования выберем АКЗ со следующими
паспортными данными и параметрами:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Значения безразмерных коэффициентов в уравнениях, рассчитанные по выражениям, приведенным выше:
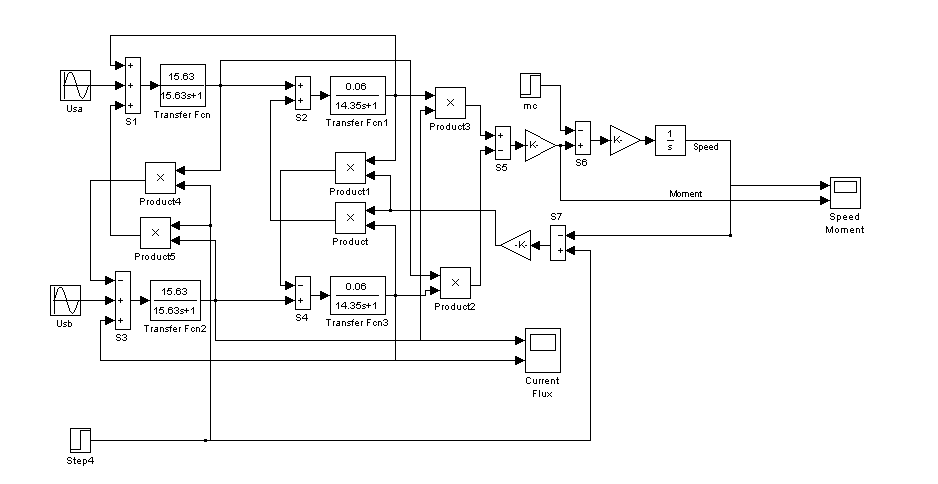
Модель АКЗ, построенная по уравнениям (1) – (6), представленная на рис. 1.
На вход модели в момент времени
![]() подаются
напряжения
подаются
напряжения
![]() ,
,
![]() ,
(
,
(![]() ),
тем самым реализуя прямой пуск.
),
тем самым реализуя прямой пуск.
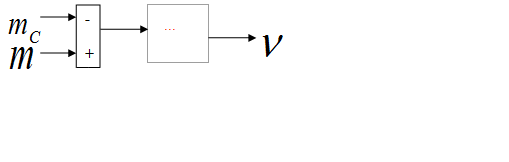
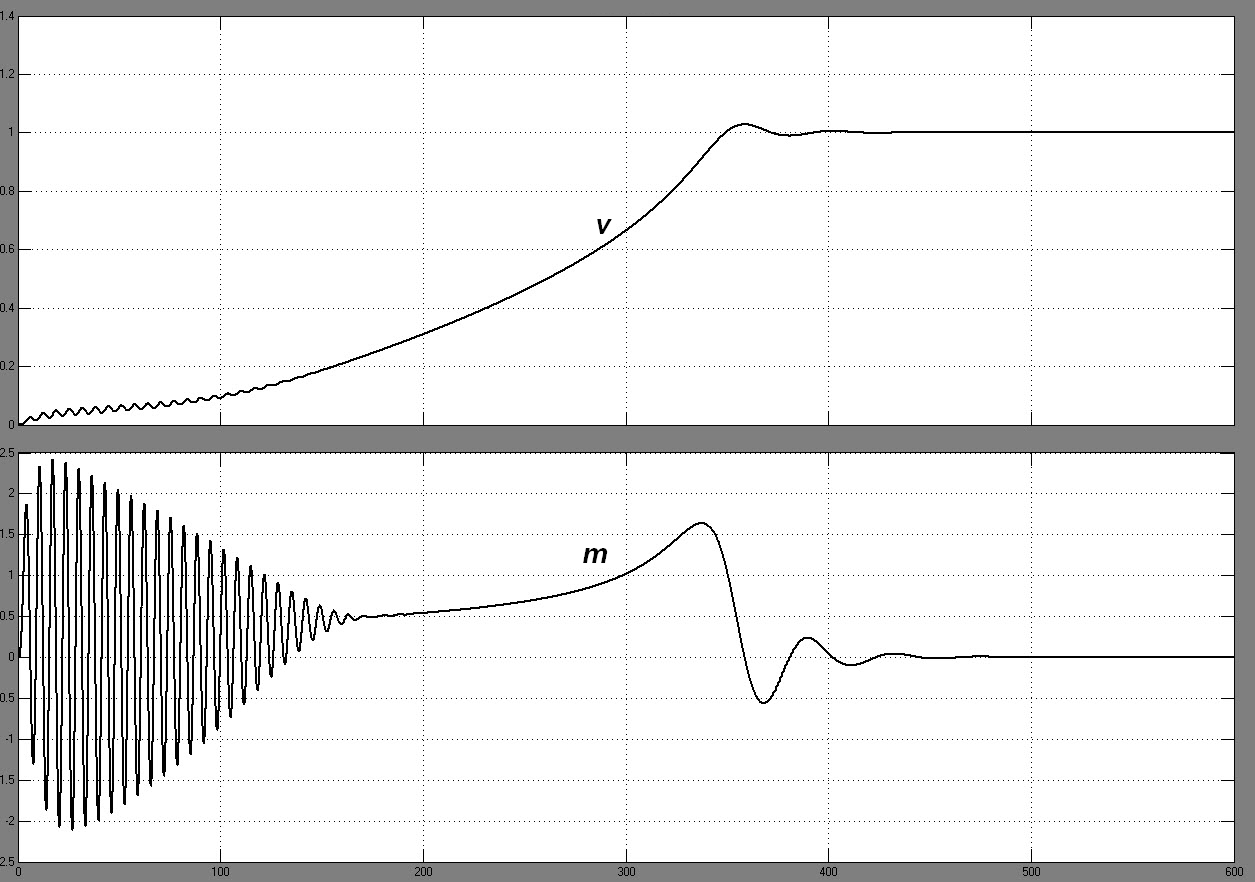
Осциллоскопы измеряют относительные значения электромагнитного момента и скорости. Результаты моделирования представлены на рис. 2. Они показывают, что при прямом пуске вначале наблюдается значительные колебания момента. Такие же колебания наблюдаются в токе и скорости. Кроме того они показывают, что при приложении момента нагрузки
Рисунок 1. Модель АКЗ в неподвижной системе координат с
переменными
![]()
Рисунок 2. Результаты моделирования, относительные значения электромагнитного момента и скорости
Литература:
Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. Екатеринбург: УРО РАН, 2000. 654 с.
Герман-Галкин С.Г. Компьютерное моделирование полупроводниковых систем Matlab 6.0: Учебное пособие. – Спб.: Корона принт. 2001. – 320с., ил.
Емельянов А.А., Бурмистров С.В., Медведев А.В., Петухов А.А. Структурная схема асинхронного двигателя в неподвижной системе координат //Инструменты развития образовательных технологий в области энергосбережения: Материалы 4-й регион. науч.-практ. конф. 27 апреля 2009., Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2009.-129с.
Емельянов А.А., Бурмистров С.В., Медведев А.В., Петухов А.А. Векторные уравнения асинхронного двигателя в различных системах координат// Автоматизация и прогрессивные технологии в атомной отрасли: VI межотраслевая научно-техническая конференция 23-25 сентября 2009., Новоуральск: ФГОУ ВПО «Новоуральский государственный технологический институт