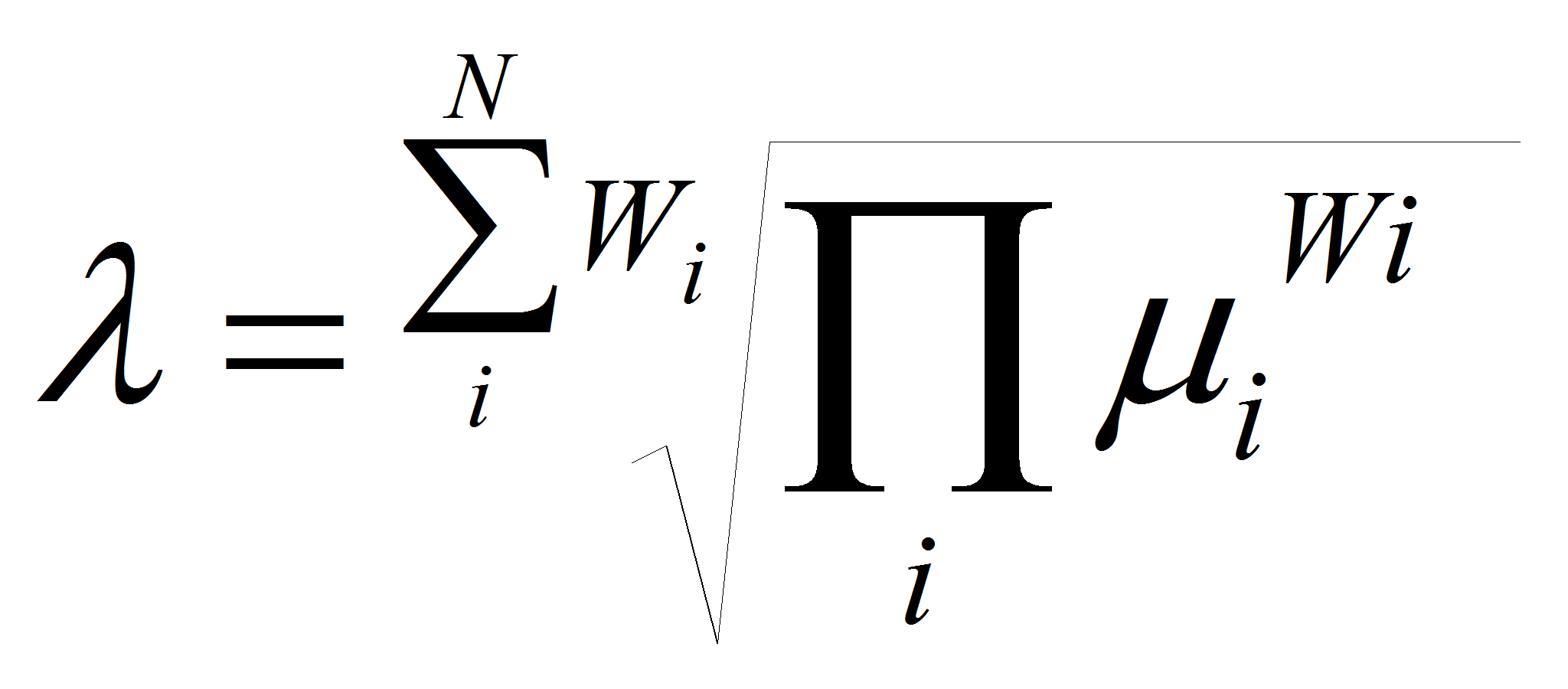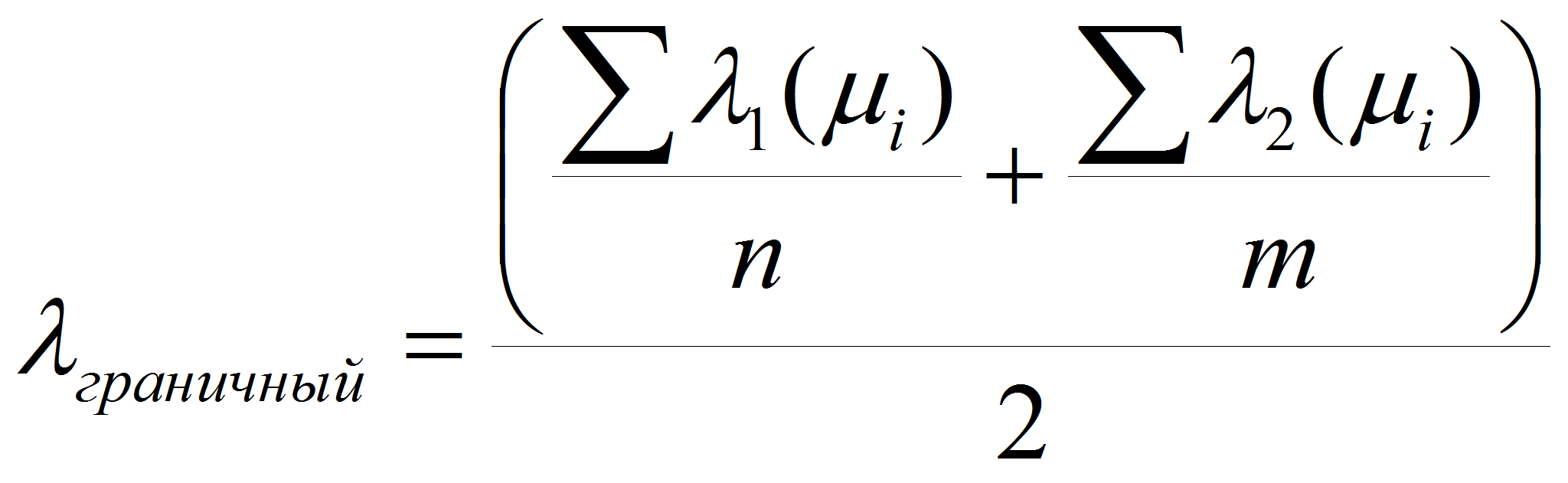Ключевые слова: интеллектуальный анализ данных, геолого-технологические мероприятия, теория нечетких множеств, функции принадлежности, комплексный критерий для выбора скважин-кандидатов, настройка кривых функций принадлежности, оптимизационная задач.
Введение
Основополагающим понятием в теории нечетких множеств является понятие нечеткого множества, которое характеризуется функцией принадлежности. Посредством нечеткого множества можно строго описывать присущие языку человека расплывчатые элементы, без формализации которых нет надежды существенно продвинуться вперед в моделировании интеллектуальных процессов. Но основной трудностью, мешающей интенсивному применению теории нечетких множеств при решении практических задач, является то, что функция принадлежности должна быть задана вне самой теории и, следовательно, ее адекватность не может быть проверена средствами теории. В каждом существующем в настоящее время методе построения функции принадлежности формулируются свои требования и обоснования к выбору именно такого построения.
Работа с несколькими факторами в теории нечетких множеств (ТНМ) сводится к формулированию и анализу комплексных критериев (КК), которые формируются на основе лингвистических переменных (высказываний) относительного каждого из факторов в рамках математической логики. Оценивается истинность высказывания, а точнее степень принадлежности фактора к высказыванию. Например, если фазифицировать значения нефтенасыщенной толщины в скважине (как пример одного из факторов влияющих на работу скважины) мы можем получить высказывание «большая нефтенасыщенная толщина», и относительно этого высказывание будем оценивать степень принадлежности численного значения от 0 до 1, где 0 – отсутствие принадлежности, 1 – полную принадлежность, промежуточные значения – степень принадлежности.
В нашем же случае комплексируются не сами значения факторов, а степень принадлежности к сформулированным нечетким лингвистическим переменным (высказываниям). Такой подход позволяет нам, во-первых, получить единый комплексный критерий который содержит в себе необходимые факторы, во вторых является достаточно гибким для получения оптимального результата.
Полученный результат в первую очередь будет зависит от функции принадлежности для каждого фактора. Поэтому важной и актуальной задачей является настройка функции принадлежности
Функции принадлежности
Конкретный вид функций принадлежности определяется на основе различных дополнительных предположений о свойствах этих с учетом специфики имеющейся неопределенности, реальной ситуации на объекте и числа степеней свободы в функциональной зависимости.
Наиболее удобными кривыми для описания функции принадлежности, являются монотонно возрастающие или убывающие сигмоиды (Рисунок 1), они удобны для задания лингвистических термов естественного языка, уравнения которых имеют вид:
где
![]() и
и
![]() - параметры сигмоиды,
- параметры сигмоиды,
![]() - величина, относительно которой формулируется ФП
- величина, относительно которой формулируется ФП
![]() .
Параметр
.
Параметр
![]() крутизна сигмоиды, при 0 сигмоида вырождается в прямую линию на
отметке 0,5, при увеличение стремиться сгрубиться до единичного
скачка. Параметр
крутизна сигмоиды, при 0 сигмоида вырождается в прямую линию на
отметке 0,5, при увеличение стремиться сгрубиться до единичного
скачка. Параметр
![]() позволяет сдвигать точку центра сигмоиды по оси Х. Кривые описанные
этим уравнением позволяют покрыть всю область, и обладают такими
полезными свойствами как непрерывность, монотонность и гладкость.
позволяет сдвигать точку центра сигмоиды по оси Х. Кривые описанные
этим уравнением позволяют покрыть всю область, и обладают такими
полезными свойствами как непрерывность, монотонность и гладкость.
Рисунок 1 – Кривая класса «сигмоид»
Известны несколько способов построения ФП [2]: метод экспертных оценок, детерминистический, вероятностный, оптимизационный, кибернетический, объективный. В настоящей работе использовался оптимизационный метод, причем данная задача формулировалась не для отдельной ФП, а для двух типов КК, при этом параметры каждой из сигмоид являлись управляющими параметрами. Изменяя один из параметров, меняется функция принадлежности и следовательно степень принадлежности параметра к высказыванию.
В качестве операции комплексирования параметром выберем наиболее категорическую операцию «И», которая в рамках математической логики выглядит в общем случае:
где
![]() - КК,
- КК,
![]() - функция принадлежности i-го
критерия,
- функция принадлежности i-го
критерия,
![]() - соответствующий вес i-го критерия,
N – количество критериев.
- соответствующий вес i-го критерия,
N – количество критериев.
В приведенной формуле комплексирование производится с учетом весовых коэффициентов, что позволяет задать значимость параметров и их отношение.
Прежде, чем сформулировать оптимизационную задачу относительно параметров ФП отметим следующее. Скважины, которые имели за всю историю работы наилучшие показатели разработки, находятся в лучших геологических условиях. Нечеткие лингвистические переменные (НЛП) формулировались таким образом, что факторы обуславливающие высокий дебит скважины, стремились к 1 (полной принадлежности), например «Большая нефтенасыщенная толщина», «большая проницаемость», «низкий коэффициент расчлененности» и т.д.
Учитывая сформулированные НЛП, логично что, средний КК
![]() для высокодебитных скважин должен стремится к максимуму, в свою
очередь КК по остальным скважинам–
для высокодебитных скважин должен стремится к максимуму, в свою
очередь КК по остальным скважинам–
![]() к минимум, т.е для решения частной задачи имеет место следующая
целевая функция.
к минимум, т.е для решения частной задачи имеет место следующая
целевая функция.
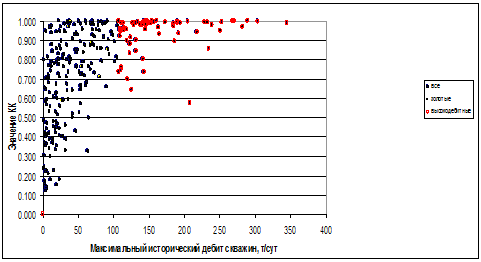
В такой постановке задача поиска решения сводится к нахождению управляющих параметров ФП. Оптимизационная задача (1) решалась с помощью оригинального программного продукта, созданного в среде программирование Visual Basic for Applications. Данная программа позволяет решать задачу, как методом Монте-Карло, так и с помощью перебора всех возможных комбинации управляющих параметров. Изменяя параметр a и b в уравнение сигмоиды, мы изменяли форму кривой, и получали различные функции принадлежности. Графически полученное решение поиска скважин с оптимальными геологическими условиями представлено на рисунке 2
Рисунок 2 – Зависимость КК и максимального дебита скважины
Как видно из рисунка 2, диапазон изменения КК для высокодебитных скважин (красные точки) от 0,6 до 1, наиболее плотное облако в районе 1. А по остальным скважинам (сини точки) КК меняется от 0,1 до 1. Скважины, у которых КК стремиться к 1 располагаются в наилучших геологических условиях.
Граничный КК после которого скважина является подходящий с геологической точки зрения вычислялся по формуле
Скважины, для которых выполняется неравенство,
![]() ,
находятся в благоприятных геологических условия, и могут работать с
высокими показателями.
,
находятся в благоприятных геологических условия, и могут работать с
высокими показателями.
Литература:
Алтунин А.Е., Семухин М.В. Иерархическая модель процесса обводнения газовых месторождений. - В сб.: "Проблемы нефти и газа Тюмени", Труды ЗапсибНИГНИ, Тюмень, вып.47, 1980, с.66-68.
Алтунин А.Е., Чуклеев С.Н. Региональнная система сбора, обработки неточной информации и принятия оперативных решений в АСУ ВПО "Тюменгазпром". Тезисы докладов научно-технической конференции "Использование вычислительной техники в решении задач повышения эффективности производства", Краснодар, 1985, с.25.
Васильков Ю.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании. – М.: Финансы и статистика, 2001. – 256 с.
Кучин Б.Л., Алтунин А.Е. Управление системой газоснабжения в осложненных условиях эксплуатации. - М: Недра, 1987, 209с.
Yager R.R. Fuzzy sets, probilities and decision. "J. of Cybern.", N10, 1980, p.1-18.