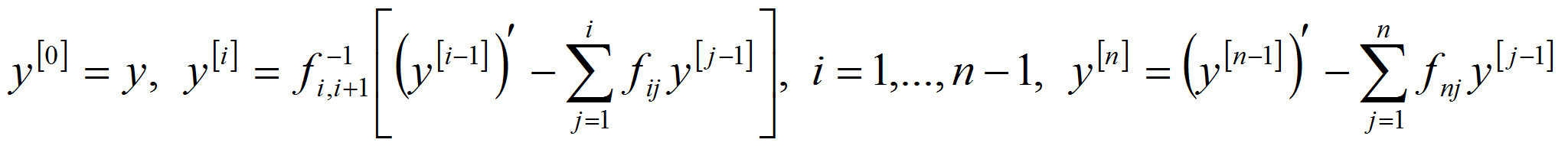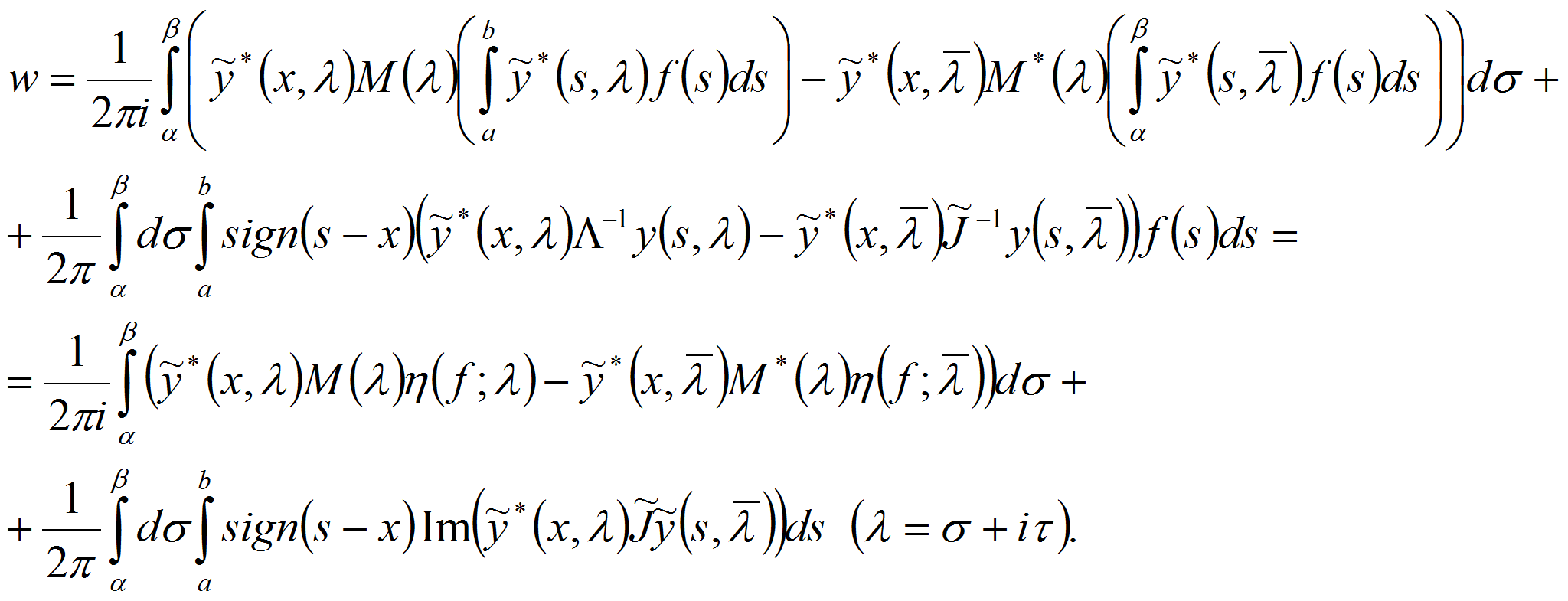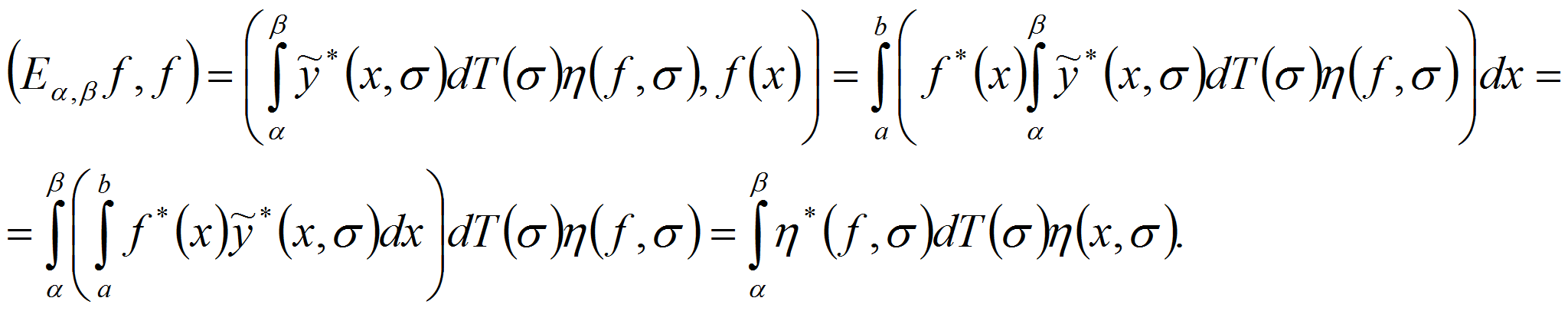Получено спектральное разложение симметрического квазидифференциального оператора, порожденного обобщенной квазидифференциальной операцией.
1. Пусть
![]() -
-
![]() - матрица, где
- матрица, где
![]() - комплекснозначных функций, определенные на
- комплекснозначных функций, определенные на
![]() и удовлетворяющих следующим условиям:
и удовлетворяющих следующим условиям:
(1)
![]() в интервале
в интервале
![]() для индексов, удовлетворяющих неравенствам
для индексов, удовлетворяющих неравенствам
![]() ;
(2)
;
(2)
![]() - локально суммируемы, т. е.
- локально суммируемы, т. е.
![]() для
для
![]() ;
;
Этот подход к определению квазипроизводных и соответствующего
формально самосопряженного квазидифференциального выражения предложен
в работе [1]. Будем считать, что функции
![]() и их квазипроизводные до
и их квазипроизводные до
![]() - го порядка включительно абсолютно непрерывны на любом компактном
подынтервале промежутка
- го порядка включительно абсолютно непрерывны на любом компактном
подынтервале промежутка
![]() .
Поскольку в дальнейшем будем рассматривать только симметрические
дифференциальные выражения, то предположим, что матрица
.
Поскольку в дальнейшем будем рассматривать только симметрические
дифференциальные выражения, то предположим, что матрица
![]() ,
кроме требований (1), (2) и (3), удовлетворяет также условию
симметричности
,
кроме требований (1), (2) и (3), удовлетворяет также условию
симметричности
![]() ,
где
,
где
![]() - матрица, сопряженная к матрице
- матрица, сопряженная к матрице
![]() ,
,
![]() - символ Кронекера. Легко убедиться, что
- символ Кронекера. Легко убедиться, что
![]() ,
где
,
где
![]() - натуральное число. Предположим, что матрица
- натуральное число. Предположим, что матрица
![]() совпадает с матрицей
совпадает с матрицей
![]() ,
если натуральное число
,
если натуральное число
![]() - четно, и с матрицами
- четно, и с матрицами
![]() ,
если натуральное число
,
если натуральное число
![]() - нечетно. Можно считать, что скалярное квазидифференциальное
выражение
- нечетно. Можно считать, что скалярное квазидифференциальное
выражение
![]() ,
где
,
где
![]() - мнимая единица, порождается матрицей
- мнимая единица, порождается матрицей
![]() .
Квазидифференциальная операция
.
Квазидифференциальная операция
![]() определяет минимальный замкнутый симметрический оператор
определяет минимальный замкнутый симметрический оператор
![]() в гильбертовом пространстве
в гильбертовом пространстве
![]() .
.
-
Для любых функций
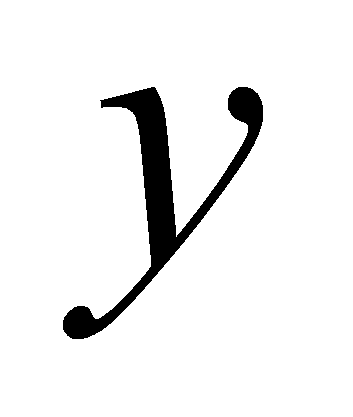 и
и
 ,
к которым применима квазидифференциальная операция
,
к которым применима квазидифференциальная операция
 ,
имеет место обобщенная формула Лагранжа
,
имеет место обобщенная формула Лагранжа
где
![]() .
Интегрируя почленно левую и правую части формулы Лагранжа (1),
получим формулу Грина
.
Интегрируя почленно левую и правую части формулы Лагранжа (1),
получим формулу Грина
![]() ,
,
где
![]() .
Заметим, что
.
Заметим, что
![]() ,
где
,
где
![]() - скалярное произведение в
- скалярное произведение в
![]() -мерном
евклидовом пространстве.
-мерном
евклидовом пространстве.
![]() - вектор-столбец, составленный из квазипроизводных
- вектор-столбец, составленный из квазипроизводных
![]() .
С помощью матрицы
.
С помощью матрицы
![]() тождество Лагранжа можно переписать в виде
тождество Лагранжа можно переписать в виде
![]() .
.
Теорема 1. Пусть![]() -
матрица, удовлетворяющая условиям (1) – (3).
-
матрица, удовлетворяющая условиям (1) – (3).
![]() -квазидифференциальное выражение.
-квазидифференциальное выражение.![]() ,
где
,
где
![]() - положительная функция на
- положительная функция на
![]() .
Тогда для любого
.
Тогда для любого
![]() ,
любого
,
любого
![]() и любых
и любых
![]() ,
существует единственное решение
,
существует единственное решение
![]() ,
заданное на
,
заданное на
![]() ,
начальной задачи
,
начальной задачи
![]()
![]() .
.
Доказательство в целом повторяет рассуждения, приведенные в монографии [2].
Теорема 2. Пусть
![]() ,
,
![]() ,
матрица
,
матрица
![]() ,
удовлетворяет требованиям (1) – (3) и условию симметричности.
Тогда для любых комплексных чисел
,
удовлетворяет требованиям (1) – (3) и условию симметричности.
Тогда для любых комплексных чисел
![]() существует функция
существует функция
![]() ,
принадлежащая области определения оператора
,
принадлежащая области определения оператора
![]() ,
такая что
,
такая что
![]()
2. Построим квазисамосопряженные расширения минимального
квазидифференциального оператора
![]() .
Предположим, что индексы дефекта оператора
.
Предположим, что индексы дефекта оператора
![]() равны. Зафиксируем какое-либо невещественное число
равны. Зафиксируем какое-либо невещественное число
![]() .
Пусть
.
Пусть
![]() - линейный оператор, отображающий дефектное подпространство
- линейный оператор, отображающий дефектное подпространство
![]() в
дефектное подпространство
в
дефектное подпространство
![]() .
Квазисамосопряженным расширением оператора
.
Квазисамосопряженным расширением оператора
![]() ,
определяемым оператором
,
определяемым оператором
![]() ,
называется оператор
,
называется оператор
![]() ,
являющийся частью оператора
,
являющийся частью оператора
![]() и имеющий своей областью определения линейное многообразие
и имеющий своей областью определения линейное многообразие
![]() элементов
элементов
![]() ,
где
,
где
![]() .
Если
.
Если
![]() - оператор, сопряженный оператору
- оператор, сопряженный оператору
![]() ,
отображающий
,
отображающий
![]() в
в
![]() ,
то соответствующие квазисамосопряженные расширения
,
то соответствующие квазисамосопряженные расширения
![]() и
и
![]() являются взаимно сопряженными. Охарактеризуем область определения
являются взаимно сопряженными. Охарактеризуем область определения
![]() оператора
оператора
![]() при помощи краевых условий. Пусть
при помощи краевых условий. Пусть
![]() - какой-либо ортонормированный базис дефектного подпространства
- какой-либо ортонормированный базис дефектного подпространства
![]() ,
а
,
а
![]() - ортонормированный базис в
- ортонормированный базис в
![]() .
Пусть в этих базисах оператору
.
Пусть в этих базисах оператору
![]() соответствует матрица
соответствует матрица
![]() .
Следовательно,
.
Следовательно,
![]() .
Рассмотрим систему вектор-функций
.
Рассмотрим систему вектор-функций
![]() ,
полагая
,
полагая
![]() .
На основании формулы Лагранжа для принадлежности вектор-функции
.
На основании формулы Лагранжа для принадлежности вектор-функции
![]() к линейному многообразию
к линейному многообразию![]() необходимо и достаточно выполнение условия
необходимо и достаточно выполнение условия
для всех
![]() .
Согласно определению квазисамосопряженного расширения
.
Согласно определению квазисамосопряженного расширения
![]() ,
откуда, в силу определения функций
,
откуда, в силу определения функций
![]() ,
поскольку
,
поскольку
![]() ,
имеем
,
имеем
![]() .
.
-
3. Как известно, каждой спектральной функции
 оператора
оператора
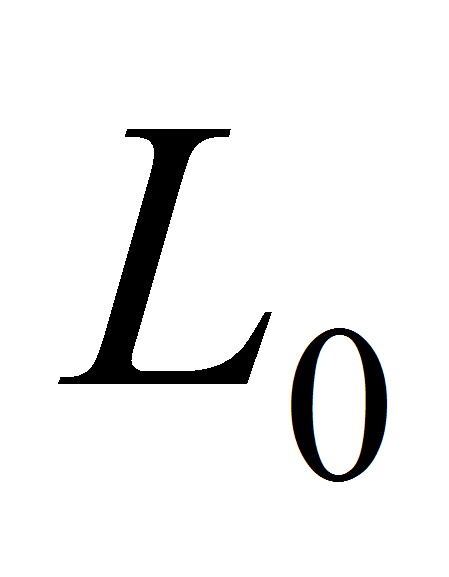 отвечает
некоторая обобщенная резольвента
отвечает
некоторая обобщенная резольвента
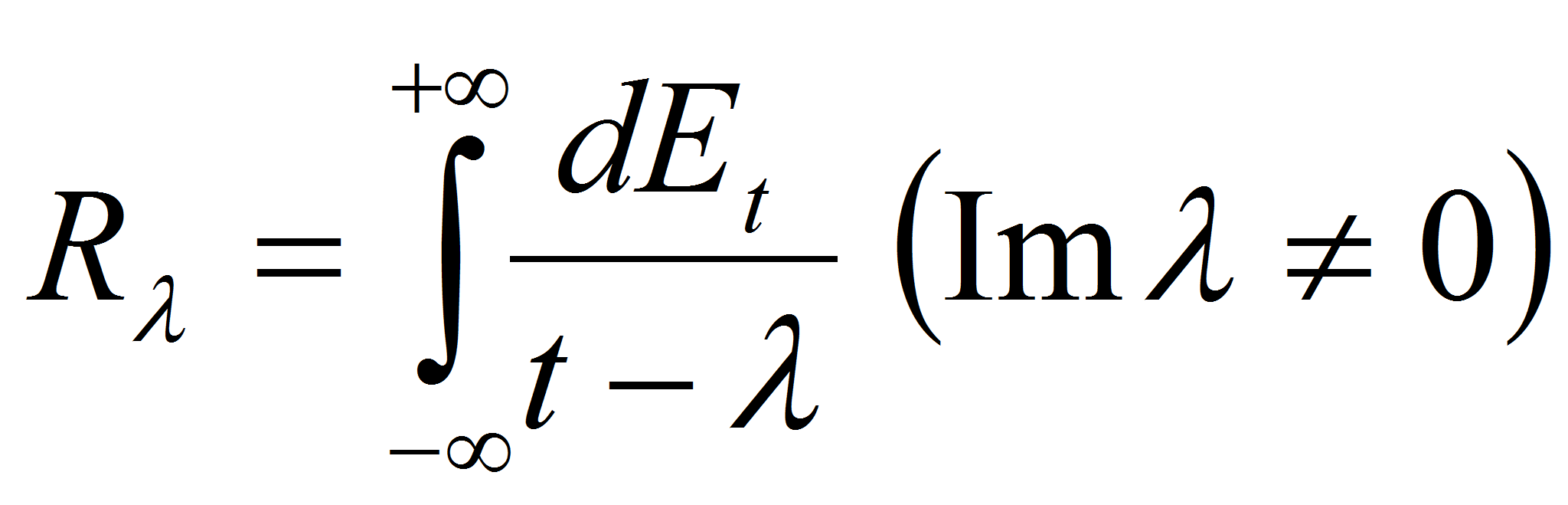 .
При помощи формулы обращения Стилтьеса спектральная функция
.
При помощи формулы обращения Стилтьеса спектральная функция
 однозначно восстанавливается по соответствующей ей обобщенной
резольвенте
однозначно восстанавливается по соответствующей ей обобщенной
резольвенте
 ;
для любых функций
;
для любых функций
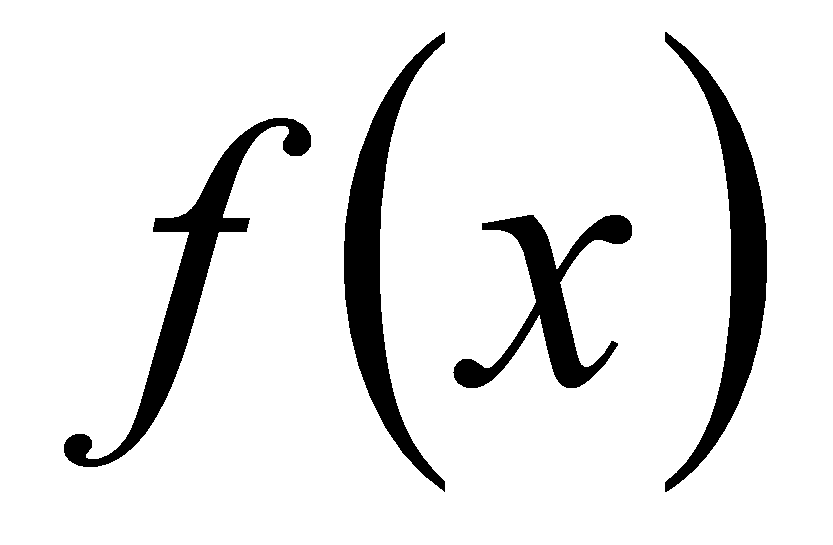 и
и
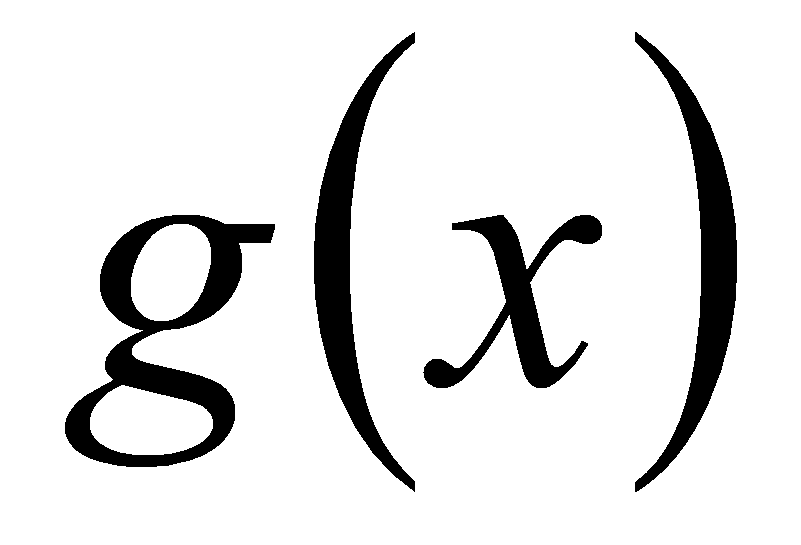 из
из
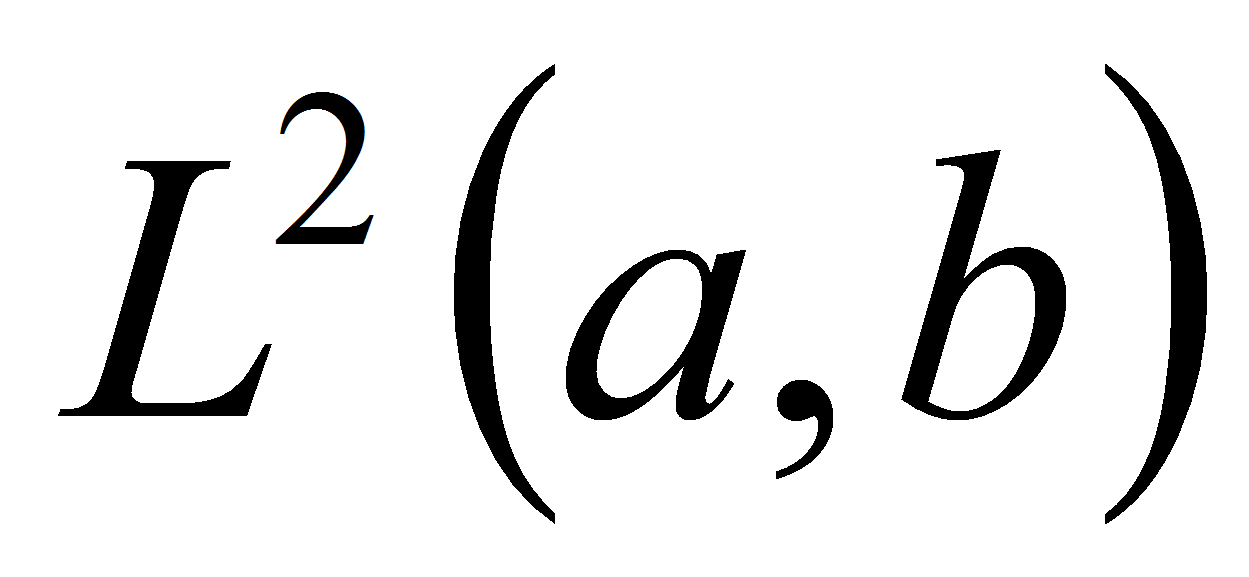 и любых вещественных
и любых вещественных
 и
и
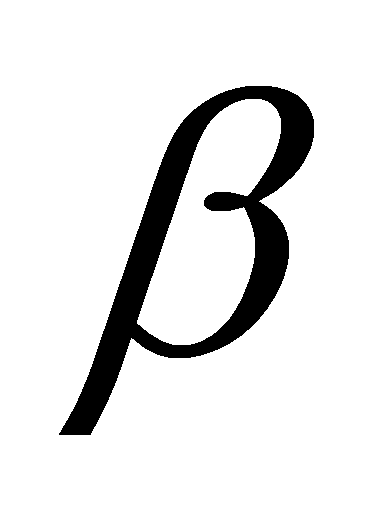 имеет место равенство:
имеет место равенство:
-
Равенство (3) позволяет построить формулу всех спектральных функций
 оператора
оператора
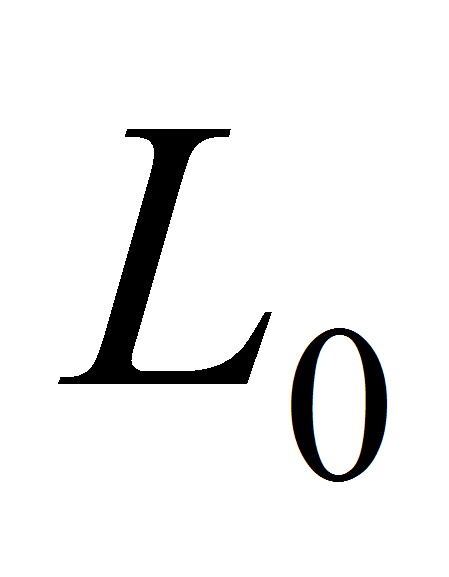 .
Пусть
.
Пусть
 - какая-либо обобщенная резольвента оператора
- какая-либо обобщенная резольвента оператора
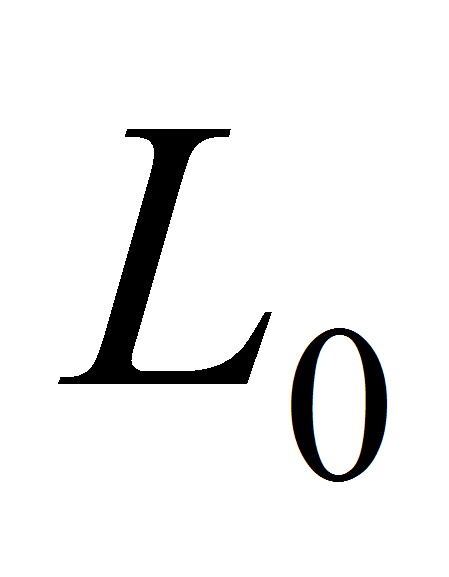 и
и
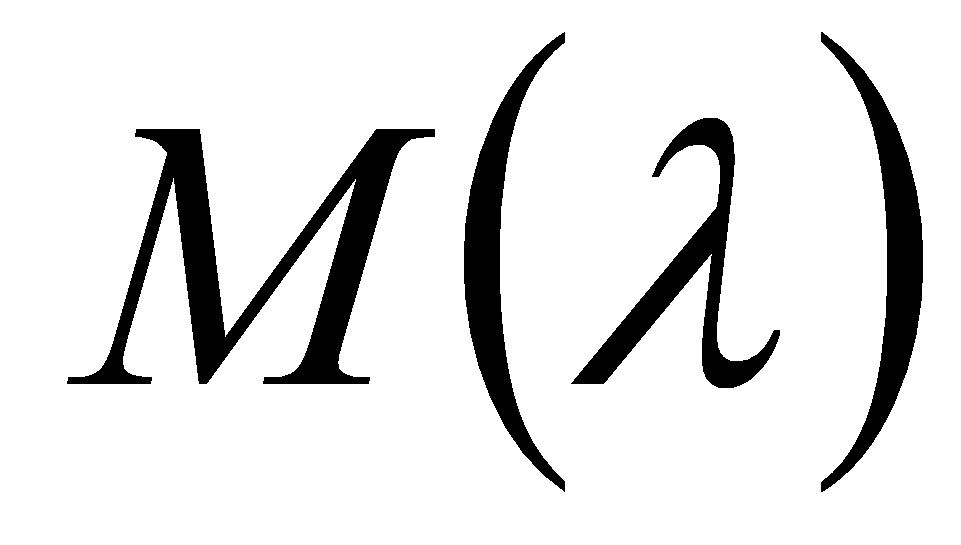 - ее характеристическая матрица. При любых вещественных
- ее характеристическая матрица. При любых вещественных
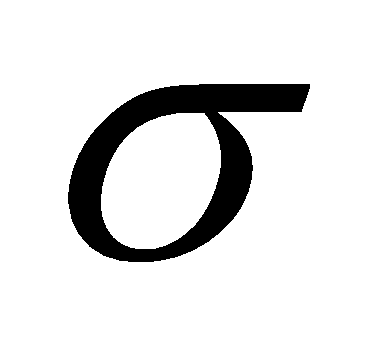 определим матрицу
определим матрицу
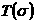 формулой
формулой
Формула (4) имеет смысл при любом вещественном
![]() и
и
![]() является неубывающей матричной функцией. Так как
является неубывающей матричной функцией. Так как
![]() регулярна в верхней комплексной полуплоскости и
регулярна в верхней комплексной полуплоскости и
![]() ,
то формула (4) имеет смысл при любом вещественном
,
то формула (4) имеет смысл при любом вещественном
![]() и
и
![]() является неубывающей матричной функцией. Матрицу
является неубывающей матричной функцией. Матрицу
![]() называют спектральной функцией распределения оператора
называют спектральной функцией распределения оператора
![]() ,
соответствующей обобщенной резольвенте
,
соответствующей обобщенной резольвенте
![]() .
.
Пусть
![]() - гильбертово пространство
- гильбертово пространство
![]() -мерных
векторных функций
-мерных
векторных функций
![]() ,
которые будем рассматривать как одностолбцевые матричные функции;
скалярное произведение в пространстве
,
которые будем рассматривать как одностолбцевые матричные функции;
скалярное произведение в пространстве
![]() определяется формулой
определяется формулой
![]() .
.
Теорема 3. Для любой функции
![]() из пространства
из пространства
![]() имеет место равенство
имеет место равенство
![]() ,
где
,
где
![]() ;
а несобственный интеграл
;
а несобственный интеграл
![]() сходится в смысле метрики пространства
сходится в смысле метрики пространства
![]() .
.
![]() Сначала предположим, что функция
Сначала предположим, что функция
![]() из
из
![]() обращается в нуль вне какого либо конечного отрезка
обращается в нуль вне какого либо конечного отрезка
![]() .
При любом невещественном
.
При любом невещественном
![]() положим
положим
![]() .
Пусть
.
Пусть
![]() и
и
![]() - произвольные вещественные числа. Введем в рассмотрение функцию
- произвольные вещественные числа. Введем в рассмотрение функцию
![]() .
.
При любом
![]() и, в силу представления
и, в силу представления
![]()
![]() .
С другой стороны, принимая во внимание, формулы для ядра обобщенной
резольвенты, получим:
.
С другой стороны, принимая во внимание, формулы для ядра обобщенной
резольвенты, получим:
Для любого фиксированного
![]() второй интеграл в правой части этого равенства стремится к нулю при
второй интеграл в правой части этого равенства стремится к нулю при
![]() .
Так как
.
Так как
![]() регулярная в верхней полуплоскости матричная функция с
неотрицательной мнимой частью то, переходя в равенстве (5) к пределу
при
регулярная в верхней полуплоскости матричная функция с
неотрицательной мнимой частью то, переходя в равенстве (5) к пределу
при
![]() при любом фиксированном
при любом фиксированном
![]() получим:
получим:
Итак, при
![]() имеет предел и в смысле слабой сходимости в
имеет предел и в смысле слабой сходимости в
![]() ,
и в смысле сходимости всюду в промежутке
,
и в смысле сходимости всюду в промежутке
![]() .
Но, как известно, оба этих предела совпадают, так что имеет место
равенство:
.
Но, как известно, оба этих предела совпадают, так что имеет место
равенство:
![]() .
.
Умножая скалярно обе части последнего равенства на
![]() и меняя затем в правой части порядок интегрирования, получим
и меняя затем в правой части порядок интегрирования, получим
Переходя здесь к пределу при
![]() и
и
![]() ,
получим соотношение
,
получим соотношение
Теорема доказана для любой вектор функции
![]() из пространства
из пространства
![]() ,
обращающейся в нуль вне конечного отрезка
,
обращающейся в нуль вне конечного отрезка
![]() .
.
Для любой функции
![]() из
из
![]() доказательство теоремы получается с помощью некоторого предельного
перехода, расширяющего носитель функции
доказательство теоремы получается с помощью некоторого предельного
перехода, расширяющего носитель функции
![]() [3,4,5].
[3,4,5].
- Литература:
Everitt, W.N. Generalized symmetric ordinary differential expressions 1: The general theory / W.N. Everitt, A. Zettl // Nieuw Archief Vood Wiskunde, 1979. - V. 27, № 3. - P. 363 – 397.
Наймарк М.А. Линейные дифференциальные операторы. – М.: Наука, 1969. – 526 с.
Филиппенко В.И. Обобщенные резольвенты неплотно заданного квазидифференциального симметрического оператора // Труды участников Международной школы-семинара по геометрии и анализу памяти Н.В. Ефимова, 5 – 11 сентября 2006 года, Ростов-на-Дону, изд-во ООО «ЦВВР», 2006. – С. 167 – 169.
Фетисов В.Г., Филиппенко В.И., Козоброд В.Н. Операторы и уравнения в линейных топологических пространствах. – Владикавказ: ВНЦ РАН, 2006. – 432 с.
Филиппенко В.И. Обобщенные спектральные функции квазидифференциального оператора // Укр. математический конгресс – 2009 / Киев: www.imath, kiev.ua/~congress 2009.