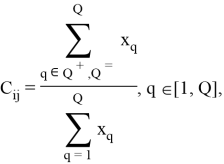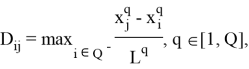В данной работе рассматривается применение метода многокритериальной оптимизации ELECTRE I для оценки степени пожарной опасности ситуации в комнатах административного помещения.
Ключевые слова: многокритериальная задача оптимизации, множество недоминируемых альтернатив, метод ELECTRE I.
В данной работе предполагается, что пожар в помещении можно охарактеризовать следующими опасными факторами — температура, дым, повышенная концентрация в воздухе углекислого и угарного газов, которые образуют множество критериев в данной задаче. В качестве объекта исследования выступает административное помещение, состоящее из шести комнат, составляющих множество альтернатив. Схема расположения комнат помещения приведена на рисунке 1.
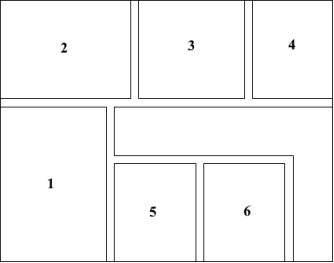
Рис. 1. Схема помещения
Таким образом, заданы множество альтернатив и множество критериев. Значения, принимаемые факторами пожара, определены в результате моделирования пожара в административном помещении с использованием интерфейса PyroSim [2] для программы Fire Dynamics Simulator (FDS). В основе FDS лежит дифференциальная модель развития пожара в помещении [3]. Данные о факторах пожара для момента времени 
от начала пожара представлены в таблице 1.
Таблица 1
Исходные данные
|
Температура |
Оптическая плотность |
Объемная доля |
Объемная доля |
|
|
1 |
206,2885 |
1,5365975 |
0,085572308 |
0,004058824 |
|
2 |
131,73926 |
1,6498153 |
0,078234618 |
0,003710036 |
|
3 |
222,54063 |
0,62055996 |
0,038004342 |
0,001791011 |
|
4 |
129,28528 |
0,85239525 |
0,042249495 |
0,001993124 |
|
5 |
344,54776 |
1,2264791 |
0,086922982 |
0,00412125 |
|
6 |
366,45868 |
1,1566811 |
0,085394465 |
0,004048609 |
Для построения множества недоминируемых альтернатив в данной работе используется метод ELECTRE I [1, с. 81–83]. В его основе лежат индексы согласия и несогласия, определяемые соотношением (1):
|
|
(1) |
где 
— индекс согласия, что 
, 
— индекс несогласия, что , 
— подмножество критериев по которым , 
— подмножество критериев по которым 
, 
— подмножество критериев по которым 
(равнозначны), 
, 
— длина шкалы 
-го критерия.
Первым шагом в построении ядра альтернатив является операция нормализации значений каждого критерия согласно формуле (2):
|
|
(2) |
В таблице 2 представлены нормализованные значения, принимаемые элементами множества критериев в каждой из комнат, образующих административное помещение.
Таблица 2
Нормализованные значения элементов множества критериев на множестве альтернатив
|
Температура |
Оптическая плотность |
Объемная доля |
Объемная доля |
|
|
1 |
0,3247 |
0,89 |
0,9724 |
0,9732 |
|
2 |
0,0103 |
1 |
0,8224 |
0,8235 |
|
3 |
0,3932 |
0 |
0 |
0 |
|
4 |
0 |
0,2252 |
0,0868 |
0,0867 |
|
5 |
0,9076 |
0,5887 |
1 |
1 |
|
6 |
1 |
0,5209 |
0,9688 |
0,9688 |
В таблицах 3 и 4 приведены значения индексов согласия и несогласия для данной задачи, определенные согласно формуле (1).
Таблица 3
Значения индексов согласия
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1 |
- |
0,74 |
0,7303 |
1 |
0,26 |
0,7303 |
|
2 |
0,26 |
- |
0,7303 |
1 |
0,26 |
0,26 |
|
3 |
0,2697 |
0,2697 |
- |
0,2697 |
0 |
0 |
|
4 |
0 |
0 |
0,7303 |
- |
0 |
0 |
|
5 |
0,74 |
0,74 |
1 |
1 |
- |
0,7303 |
|
6 |
0,2697 |
0,74 |
1 |
1 |
0,2697 |
- |
Таблица 4
Значения индексов несогласия
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1 |
- |
0,11 |
0,0685 |
0 |
0,5829 |
0,6753 |
|
2 |
0,3144 |
- |
0,3829 |
0 |
0,8973 |
0,9897 |
|
3 |
0,9732 |
1 |
- |
0,2252 |
1 |
0,9688 |
|
4 |
0,8865 |
0,7748 |
0,3932 |
- |
0,9133 |
1 |
|
5 |
0,3013 |
0,4113 |
0 |
0 |
- |
0,0924 |
|
6 |
0,3691 |
0,4791 |
0 |
0 |
0,0678 |
- |
Для удаления доминируемых альтернатив согласно методу ELECTRE I необходимо ввести условия, отраженные в формуле (3):
|
|
(3) |
где 
— пороговые уровни согласия, 
— пороговые уровни несогласия, которые задаются лицом, принимающим решения.
Для значений
и 
построен граф предпочтения. Отношение доминирования на графе отражено стрелкой, направление которой указывает на доминируемую альтернативу. Альтернативы, в которые не входит ни одна стрелка образуют ядро недоминируемых альтернатив и обозначаются зеленым цветом, все остальные альтернативы — красным.
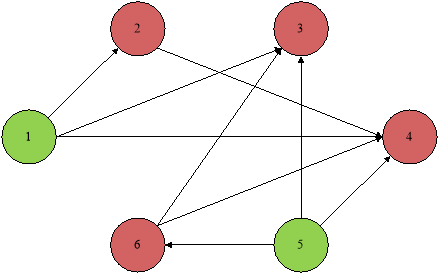
Рис. 2. Граф предпочтения для данной задачи
Таким образом, в ядро входят две альтернативы — первая и пятая комнаты, которые при данных значениях и нельзя сравнить. Также стоит отметить, что в ядро не вошла шестая альтернатива. Несмотря на высокие значения, принимаемые вторым, третьим и четвертым критериями, она доминируется пятой альтернативой. Также очевидным является тот факт, что третья и четвертая альтернативы являются доминируемыми и не попадут в ядро альтернатив, ввиду низких значений всех четырех критериев по сравнению с остальными альтернативами.
Литература:
1. Болотин И. В. Системный анализ, оптимизация и принятие решений. Практикум: учебное пособие / Под ред. В. Н. Козлова. — СПб.: Изд-во Политехн. ун-та, 2010. — 111 с.
2. Контарь Н. А. Карькин И. Н. Примеры построения расчетных моделей для решения различных задач пожарной безопасности зданий и сооружений. — Екатеринбург, 2016. — 220с.
3. Применение полевого метода математического моделирования пожаров в помещениях: Методические рекомендации. — М.: ВНИИПО, 2003. — 35 с.
