В настоящее время достижения математики и современной вычислительной техники находят все более широкое применение в планировании экономических процессов. Однако с развитием общества произошло резкое увеличение объемов производства, появилась необходимость решать задачи планирования и управления, выработки прогнозов на будущее. Увеличилось количество информации, которую необходимо учитывать при решении таких задач, а вместе с этим и увеличилось множество причин, приводящих к невыполнению плана в установленные договором сроки. Под действием внешних и внутренних факторов в нашей задаче нахождения оптимального плана производства коэффициенты со временем могут меняться, и тогда решение задачи становится уже не актуальным. В связи с этим поставлена задача исследовать, как влияют случайные изменения коэффициентов задачи на план производства и как найти новое оптимальное решение при срыве производства.
Пусть некоторый производственный объект может выпускать n различных видов продукции (товаров). При производстве этих товаров предприятие ограничивается имеющимися ресурсами, их количества равны соответственно 
условных единиц. Известна экономическая выгода от продукции каждого вида, исчисляемая ценой реализации 
. Известны также технологические коэффициенты 
, которые указывают, сколько единиц i-го ресурса требуется для производства единицы продукции j-го вида. [1].
Пусть задача линейного программирования решена и вектор X=(x_1,x_2,…,x_n) — ее оптимальное решение.
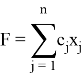
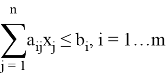
Необходимо выяснить, как возмущения по вероятности коэффициентов матрицы повлияют на значение целевой функции. Нас интересуют случаи, когда ранг рандомизированной системы ограничений остается прежним и тогда рассматривается отклонение от прежнего решения с невозмущенными коэффициентами. Если же ранг матрицы изменится, то это приведет к событию, не соответствующему поставленной задаче.
Будем называть реализацию случайного отклонения допустимой, если при ней оптимальный план, полученный на последнем шаге симплекс-метода, остается оптимальным. Кроме того, мы не рассматриваем те планы производства, в которых сумма затрат превосходит полученной прибыли, т. е. значение целевой функции: 
, ведь тогда такой план принесет лишь убытки, хоть и будет оптимальным.
Таким образом, можно сформулировать задачу линейного программирования используя введенные определения:
коэффициенты аij и bi являются независимыми случайными величинами, а коэффициенты сj остаются постоянными
…
где коэффициенты выглядят следующим образом:
Так как при возмущениях оптимальное решение должно остаться оптимальным, то
С каждым случаем розыгрыша случайных величин в матрице получаются конкретные значения коэффициентов системы ограничений, что позволяет в дальнейшем использовать стандартный симплекс-метод для нахождения оптимального значения целевой функции.
Мы рассматриваем стохастическую задачу линейного программирования, то есть первоначальные коэффициенты системы ограничений нам известны, как и коэффициенты целевой функции. Поэтому нам известен оптимальный вектор
и значение целевой функции 
эти величины не являются случайными.
Необходимо произвести оценку дисперсий случайных возмущений коэффициентов, чтобы в дальнейшем оценить возможные потери плана и выяснить при каких допустимых значениях оптимальный план остается оптимальным.
Вычислим математическое ожидание левой и правой части ограничения при i=1, j=2 (аналогичные выводы будут верны и при i=m, j=n):
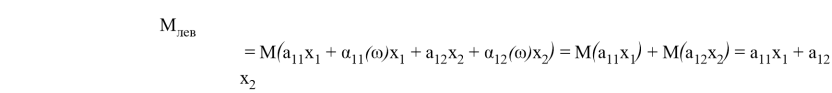
Т. к. 
, то это соотношение совпадает с исходным ограничением. Посчитаем дисперсию:
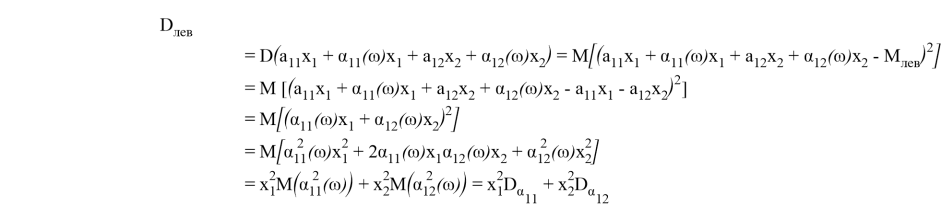
Т. к. 
, то:
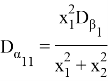
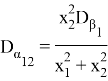
Аналогичные оценки можно получить и для случая, когда матрица коэффициентов имеет размерность 
, ведь все случайные возмущения попарно независимы:
Теперь, когда мы вывели зависимость дисперсий коэффициентов системы от дисперсий коэффициентов ограничений, можно определить доли каждой величины 
в 
. Величины 
известны нам из решения детерминированной задачи, а мы определяем сами, тогда можем найти:
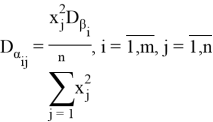
Вычислив дисперсии случайных возмущений каждого из коэффициентов и учитывая, что их математические ожидания равны нулю, можно разыграть эти случайные величины. Далее решаем новую детерминированную задачу линейного программирования с помощью симплекс-метода с новыми коэффициентами: получаем новый оптимальный вектор 
и новое значение целевой функции 
.
Планирование может производиться на разные периоды времени, в зависимости от требований заказчика: неделя, месяц, год и т. п. Например, разработан план на 1 год. Если в некоторой временной точке (меньше года) происходит увеличение отклонения целевой функции больше, чем полученная оценка дисперсии 
, то тогда требуется пересмотр плана, учитывая новую . С экономической точки зрения, пересмотр плана подразумевает вмешательство плановых служб предприятия. Далее формулируются новые требования к коэффициентам системы и целевой функции для обеспечения наибольшей разности 
и вырабатывается новый план на оставшийся период времени по схеме, рассмотренной выше.
Разделив число успешных опытов q на их общее число Q, получим вероятность выполнения плана без каких-либо срывов производства или нарушений сроков:
Результаты исследования позволяют учитывать случайные отклонения в процессах для решения экономических задач и использовать их в прогнозировании достижения оценок.
Литература:
- Юдин Д. Б., Гольштейн Е. Г. Задачи и методы линейного программирования. М.: Советское радио, 1961.
