Рассмотрена математико-экономическая модель работы современной фирмы, представленная системой дифференциальных уравнений, показывающая инвестирование в бизнес посредством кредитной ссуды. Для модели создана комбинированная стратегия прогнозирования, позволяющая анализировать динамику развития фирмы и выбирать оптимальные параметры по кредиту и деятельности предприятия.
Ключевые слова: моделирование, стратегия развития, предприятие, кредитные ресурсы, оптимальные выплаты, уровень долга, объем производства.
Будем использовать математико-экономическую модель фирмы с линейной функцией издержек, рассмотренную в [1], отражающую связь долга по кредиту и объема производства:
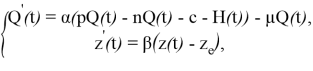 (1)
(1)
где ![]() =
=![]() =
=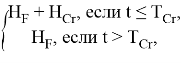
время погашения долга по кредиту вычисляется:
![]() ,
,
которое получается из второго уравнения системы (1) следующим образом:
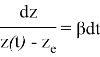
и далее,
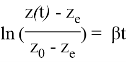
откуда получаем уравнение
![]() , (2)
, (2)
которое определяет динамику долга.
Начальные условия
![]() (3)
(3)
которые определяют особенность системы дифференциальных уравнений, что начальные точки всех фазовых траекторий находятся в фазовой плоскости ![]() на прямой:
на прямой:
![]()
Задача. Разработка плана развития и расчет оптимальных выплат по кредиту за заданное время на втором этапе развития с учетом перспективы полного погашения долга предприятия при уже достигнутом значении максимального долга в модели (1) с начальными условиями (3).
Теоретический смысл данной стратегии заключается в том, что предприятие на данный момент уже имеет некоторый достигнутый ненулевой уровень производства и долга, и ему нужно погасить этот долг, чтобы выйти на новый этап развития. То есть, на первом этапе предприятие активно развивается, увеличивая объем производства, а уже на втором этапе уменьшает долг до нуля. Это достигается посредством смены структуры распределения прибыли, в данном случае возрастания выплат по кредитному договору, которые и будут являться управлением. Здесь производится расчет оптимальных выплат, которые позволят за произвольно заданное количество времени снизить уровень долга до нулевого значения.
Первый этап: построим прямую максимального долга для модели (1):
где ![]() — произвольно заданное значение максимального долга. Его определяет руководитель предприятия.
— произвольно заданное значение максимального долга. Его определяет руководитель предприятия.
На основании условий рассматриваемой стратегии развития производится расчет времени достижения интегральной кривой системы уравнений (1) заданного значения с учетом начальных данных (3). На следующем шаге полученное время ![]() позволяет определить объем производимой продукции предприятия:
позволяет определить объем производимой продукции предприятия:
![]() (4)
(4)
где ![]() ,
, ![]() .
.
Второй этап: на следующем шаге из конечной точки первого этапа строятся фазовые траектории развития по формулам (2) и (4), начальные точки которых также лежат в фазовой плоскости ![]() на прямой
на прямой ![]() , где
, где ![]() выбирается наиболее подходящим образом.
выбирается наиболее подходящим образом.
В стратегии подразумевается сведение долга к нулевому значению, поэтому нужно выполнить построение прямой минимального долга:
![]()
где ![]() — произвольно заданное значение минимального уровня долга предприятия.
— произвольно заданное значение минимального уровня долга предприятия.
Далее производится подсчет оптимальной выплаты по кредиту, посредством которой долг будет погашен
![]() .
.
Также на основании выплаты по кредиту производится расчет уровня производства, на который выйдет предприятие в результате.
Уровень развития предприятия считается наиважнейшим смыслом его существования. Поэтому актуальной задачей является изучение способов его увеличения. Вариации развития фирмы с различными условиями, начальными данными и планами на будущее дают возможность сделать выводы о перспективности параметров стратегии и выбрать оптимальные из них.
Литература:
1. Лебедев В. В., Лебедев К. В. Исследование кредитного механизма, используемого для развития рынка новой продукции, на основе математического моделирования // Анализ, моделирование, управление, развитие экономических систем: сборник научных трудов VI Международной школы-симпозиума АМУР-2012, Севастополь, 17–23 сентября 2012 / отв. ред. М. Ю. Куссый, А. В. Сигал — г. Симферополь: Изд-во ТНУ им. В. И. Вернадского, — 2012. — С. 227–229.







