В этой статье рассматриваются вопросы выполнения нечеткого поиска, извлечение семантики слов и применение векторной модели для расширения поиска. Изложены общие идеи при решении поставленной задачи, приводятся алгоритмы с их последующей реализацией и их результатами работы.
Ключевые слова: нечеткий поиск, векторизация слов, word embedding, word2vec.
Одной из проблем при обработке поисковых запросов, является тот факт, что написание слова не связано с его смысловым значением. Как следствие, даже применение морфологического и синтаксического анализа запроса может оказаться недостаточно для разрешения имеющейся неопределенности.
В качестве возможного решения этой проблемы, рассматривается перенос слов в векторное пространство (word embedding), при осуществлении которого семантически близкие слова должны получить близкие значения векторов. Такой способ представления слов позволяет реализовать нечеткий поиск, учитывающий не только синтаксис, но и семантику запроса.
Основные предположения
Для решения задачи нечеткого поиска, в классическом подходе применяются различные методы и алгоритмы, например: расстояние Левенштейна (и его модификации), метод n-грамм, алгоритм расширения выборки (ввод искусственных ошибок в запрос) и другие. Все эти методы объединяет тот факт, что они основаны на представлении слов как последовательности символов, а не через их значение.
Если предположить, что можно расширить область поиска за счет учета семантики запроса, то перечисленных методов будет недостаточно. Итак, необходимо рассмотреть модель, в которой каждое слово связано со своим контекстом и может рассматриваться не только как конкретная последовательность символов, но и через определение взаимного расположения с другими словами.
Для осуществления подобного преобразования можно воспользоваться векторной моделью, представляющей слова точками в многомерном пространстве. В таком случае становятся возможны следующие подходы: поиск по модифицированному запросу, в котором слова заменяются на похожие (в векторном пространстве); поиск по соотношению между словами (вычисляется арифметически по векторам, затем можно осуществлять поиск по этому значению или вектору); поиск по общим ближайшим соседям (можно искать не только по соседям первого порядка (только соседи), но и через несколько порядков (соседи соседей)); и другие.
Реализация итестирование
Программная реализация выполнена на языке Python, для построения векторной модели используется реализация модели word2vec из библиотеки gensim, предобработка осуществляется методами из библиотеки nltk. Обучение модели произведено на датасете OpinRank Data [5].
После получения векторной модели, реализуем отдельные методы для работы с текстом. Например, на следующем листинге описана функция, которая получает на вход векторную модель и предложение, а на выходе формируется предложение с заменой слов на ближайших соседей.

Следует отметить, что некоторые слова могут отсутствовать в модели, поэтому для них срабатывает исключение, которое переносит подобные слова в итоговое предложение без изменений. При необходимости, в функцию могут быть внесены улучшения, такие как определение минимального порога схожести слов, отдельная обработка ключевых слов и т. п. Для проверки выполним исходную функцию.
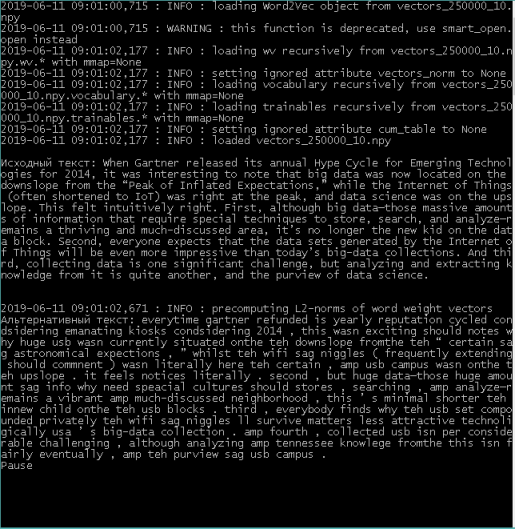
Рис. 1. Метод модификации предложения
Применение векторной модели не ограничивается поиску с учетом синонимов и модификации предложений. Одним из преимуществ векторов является то, что это набор числовых значений, а значит к ним применимы арифметические операции. Рассмотрим это на примере следующего алгоритма:
0) Получить два сравниваемых предложения, разбить на отдельные слова. Объявить массивы для сохранения результатов. Переменная i = 1.
1) Выбрать слова из первого предложения под номерами i и i+1 как w1 и w2. Переменная j = 1.
2) Выбрать слова из второго предложения под номерами j и j+1 как w3 и w4.
3) Для каждого из слов (w1, w2, w3, w4) получить вектор (v1, v2, v3, v4)
4) Вычислить разницу векторов в словосочетании (v1 минус v2, аналогично v3 минус v4). Эта разность считается отношением слов в паре, чем ближе вектора разности, тем больше похожи выбранные пары. Для этого вычисляется взвешенная поэлементная абсолютная разность полученных векторов.
5) Если найдено соответствие между двумя парами, записать в массив результатов. Если j+1 меньше длины второго предложения, прибавить к переменной j единицу, перейти к шагу 2), иначе к шагу 6).
6) Если i+1 меньше длины первого предложения, прибавить к переменной i единицу, перейти к шагу 1), иначе завершить поиск и вывести результаты.
Фактически, описанный алгоритм ищет похожие словосочетания в двух предложениях. После реализации метода, необходимо его протестировать. Для этого возьмем два текста из разных источников и выполним функцию, реализующую алгоритм.
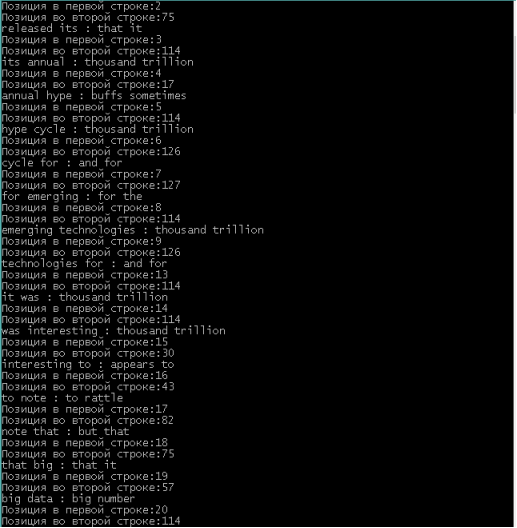
Рис. 2. Пример поиск пар словосочетаний
Можно сделать очевидное замечание, что найденные пары могут относиться к разному контексту. Поэтому следует рассматривать модифицированный алгоритм. Возможны следующие варианты: поиск относительно ключевых слов (в некотором окне, например, пять слов до и после), сравнение общих соседей (если у пар слов нет общих соседей, то скорее всего они относятся к разному контексту), рассмотрение троек слов (можно построить три пары, которые должны иметь аналоги во втором тексте) и т. п.
Заключение
В этой статье рассматривалась проблема осуществления поиска с применением векторизации слов. Преимущества такого подхода состоят в отсутствии необходимости вручную составлять словари или размечать текст, возможность перехода от символьных операций к числовым. Основным недостатком является необходимость использования больших выборок текста при обучении. Также следует отметить, что результаты вычислений в векторной модели необходимо интерпретировать и оценить для получения адекватных результатов.
Литература:
- Автоматическая обработка текстов на естественном языке и анализ данных: учеб. пособие / Большакова Е. И., Воронцов К. В., Ефремова Н. Э., Клышинский Э. С., Лукашевич Н. В., Сапин А. С. — М.: Изд-во НИУ ВШЭ, 2017. — 269 с.
2. Библиотека NLTK http://www.nltk.org/
- Adam Geitgey Natural Language Processing is Fun! medium.com/@ageitgey/natural-language-processing-is-fun-9a0bff37854e
- Madhu Sanjeevi Chapter 9.2: NLP — Code for Word2Vec neural network(Tensorflow). https://medium.com/deepmath-machine-learning-ai/chapter-9–2-nlp-code-for-word2vec-neural-networktensorflow-544db99f5334
- Корпус текстов OpinRank Data. kavita-ganesan.com/entity-ranking-data/







