В работе [1] авторы представили метод определения топологических компонентов диаграмм узловых путевых структур с помощью полиномиального инварианта Джонса, где на первом этапе решения задачи комбинаторного анализа схемы развязки моделируются в топологические узлы посредством соединения путей между собой с соблюдением следующих двух условий:
- Соединения путей не должны образовывать новых двойных точек самопересечения (путепроводов);
- Полученные топологические узлы (тривиальные или нетривиальные) должны быть едины, то есть должны представлять собой зацепление, состоящее из одной компоненты.
Первое условие легко достигается. Второе условие для сверхсложных схем развязок возможно выполнить, рассчитав для полученных топологических узлов так называемые инварианты. Инвариант узла представляет собой числовое (но чаще всего алгебраическое) выражение, которое присваивается в соответствие узлу, и остается неизменным при различных непрерывных преобразованиях этого узла. Для решения комбинаторной задачи нахождения всех возможных вариантов соединения путей в развязке требуется поочередное выполнение именно третьего движения Рейдемейстера, которое и является этим самым непрерывным преобразованием.
Если рассчитанный инвариант будет соответствовать тривиальному или нетривиальному узлу, значит пути в схеме развязки смоделированы в топологический узел правильно. На рис. 1 представлены графические примеры диаграмм тривиального и нетривиального узлов.

Рис. 1. Диаграммы тривиального и нетривиального узлов
В каждой схеме развязки (которую также можно назвать перекрестком) пересекаются образы проекций разных дуг («кусочков») топологического узла. Такие типы символического изображения дуг узлов называются соответственно переходами и проходами (рис. 2)
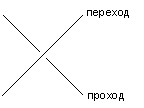
Рис. 2. Графическое обозначение перехода и прохода
Под сложностью железнодорожной развязки (как и топологического узла) будем понимать минимальное количество перекрестков ее плоской диаграммы.
Задача комбинаторного анализа будет сводиться к выполнению на плоской диаграмме топологического узла всех возможных третьих движений Рейдемейстера. Другими словами, диаграммы ![]() топологических узлов, представляющих собой развязки линий, могут быть преобразованы друг в друга посредством применения конечной последовательности третьих движений Рейдемейстера
топологических узлов, представляющих собой развязки линий, могут быть преобразованы друг в друга посредством применения конечной последовательности третьих движений Рейдемейстера ![]() .
.
Чтобы в этом убедиться, достаточно познакомиться с таким понятием, как изотопический класс, то есть всеми возможными узлами, имеющими одинаковый инвариант. В этом случае говорят, что узлы изотопны данному конкретному узлу.
Комбинаторный перебор всех возможных вариантов соединения и расположения путей в схеме развязки не будет выходить за пределы данного ему изотопического класса, поскольку само третье движение Рейдемейстера не меняет изотопического класса.
На рис. 3 представлен пример моделирования схемы развязки железнодорожного узла треугольного типа в виде топологического узла, как вложения окружности ![]() в трехмерное евклидово пространство
в трехмерное евклидово пространство ![]() . В действительности существует множество методов кодирования такого узла, например, с помощью групп кос, диаграмм Гаусса или так называемых d-диаграмм.
. В действительности существует множество методов кодирования такого узла, например, с помощью групп кос, диаграмм Гаусса или так называемых d-диаграмм.
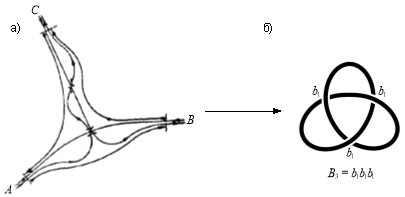
Рис. 3. Пример графического представления схемы развязки подходов линий в железнодорожных узлах треугольного типа: ![]() в общепринятом — геометрическом виде;
в общепринятом — геометрическом виде; ![]() в алгебраическом — в виде топологического узла
в алгебраическом — в виде топологического узла
Рассмотрим способ кодировки и свойства этого топологического узла с помощью диаграмм Гаусса. Для дальнейшего рассмотрения сформулируем определение.
Определение. Возьмем узел и его плоскую диаграмму, отметим на ориентированной окружности прообразы всех двойных точек самопересечения плоской диаграммы узла. Пары, соответствующие одной двойной точке диаграммы, соединим стрелкой, то есть хордой с направлением, по следующему правилу: ориентируем хорду от прообраза перехода к прообразу прохода. Каждой полученной стрелке сопоставим знак «+» или «-» в зависимости от типа перекрестка в соответствующей двойной точке диаграммы узла:
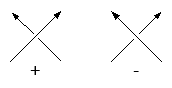
Построенный объект называется диаграммой Гаусса.
На рис. 4 приведен пример кодировки топологического узла с помощью диаграммы Гаусса.
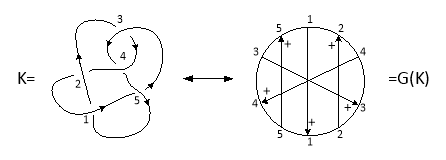
Рис. 4. Пример кодировки топологического узла с помощью диаграммы Гаусса
Отметим также, что любой узел можно восстановить по диаграмме Гаусса с точностью до изотопии.
Диаграммы Гаусса обладают одной примечательной особенностью, которую можно объяснить следующей теоремой.
Теорема. Если диаграмма Гаусса кодирует топологический узел, то для любой стрелки все стрелки, которые ее пересекают, можно разбить на пары сонаправленных стрелок различных знаков или противоположно направленных стрелок одного знака.
Необходимо сказать, что не любая диаграмма с хордами, стрелками и со знаками «+» и «-» являются гауссовой диаграммой некоторого топологического узла ![]() . Пример диаграммы, не являющейся таковой ни при какой расстановке стрелок и знаков, показан на рис. 5.
. Пример диаграммы, не являющейся таковой ни при какой расстановке стрелок и знаков, показан на рис. 5.
Рис. 5. Изображение диаграммы, которая не является диаграммой Гаусса
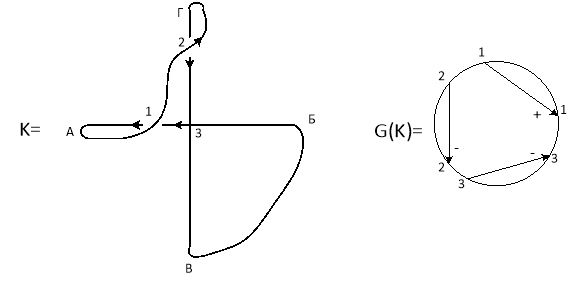
Рис. 6. Пример кодировки диаграммой Гаусса схемы развязки железнодорожного узла крестообразного типа
Рассмотрим далее, как на диаграммах Гаусса происходит операция третьего движения (преобразования) Рейдемейстера, необходимая для комбинаторного анализа всех возможных вариантов расположения и соединения путей в развязках железнодорожных узлов. На рис. 6 представлен пример кодировки схемы развязки крестообразного типа.
Третье преобразование Рейдемейстера предусматривает перекидывание нити через двойную точку самопересечения под номером 3 на противоположную сторону. При этом суммарное число точек самопересечения не меняется. Полученная схема развязки и ее диаграмма Гаусса представлена на рис. 7.

Рис. 7. Выполнение третьего движения Рейдемейстера на схеме развязки линий в железнодорожном узле крестообразного типа и ее диаграмме Гаусса
Если в представленном узле поменять ориентацию (направление обхода узла), то на диаграмме Гаусса эти приведет к изменению направления окружности на противоположное. При этом знаки стрелок не изменятся (рис. 8).
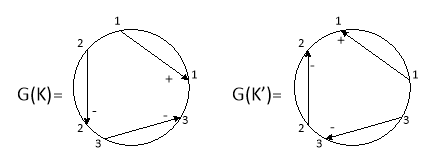
Рис. 8. Замена ориентации направления обхода узла на диаграмме Гаусса
В случае, когда на схеме развязки линий в железнодорожном узле в путепроводах меняется проход с переходом, то топологический узел ![]() становится либо зеркальным узлом
становится либо зеркальным узлом ![]() , либо иным, не изотопным
, либо иным, не изотопным ![]() . В случае зеркальных узлов
. В случае зеркальных узлов ![]() диаграммы Гаусса отличаются только знаками (знак каждой хорды меняется на противоположный, так как при взятии зеркального образа узла изменяется тип каждого перекрестка) (рис. 9).
диаграммы Гаусса отличаются только знаками (знак каждой хорды меняется на противоположный, так как при взятии зеркального образа узла изменяется тип каждого перекрестка) (рис. 9).
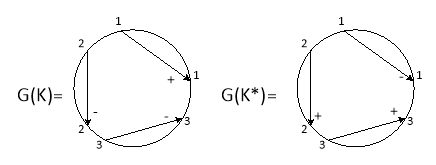
Рис. 9. Замена перекрестков на диаграмме Гаусса
Таким образом можно констатировать, что задачу тривиального перебора всех возможных вариантов пересечения железнодорожных путей в развязках можно производить также и на диаграммах Гаусса, предварительно закодировав комбинаторную структуру рассматриваемых схем развязок. По аналогии задача может быть так же решена на группах кос и d-диаграммах.
Литература:
- Шмаль С. Н., Янев Ж., Павлова Е. Ю., Куртикова А. Р. Определение топологических компонентов диаграмм узловых путевых структур с помощью полинома Джонса // Молодой ученый. — 2017. — № 49. — С. 1–4.







