Построение карт диспаратности (disparity map, карта смещений) является предварительным этапом в задачах компьютерного зрения, в частности, в автоматической трехмерной реконструкции сцен по набору изображений. Существует множество алгоритмов построения трехмерных моделей, но все они предполагают наличие стереопары изображений и откалиброванных камер. Для калибровки необходимо знать внутренние параметры камер и их взаимное расположение в пространстве. В таком случае эта задача решается через тривиальные преобразования. В данной статье предложен метод построения карты смещений на основе метода «слабой» калибровки (когда параметры камеры неизвестны) для ректификации изображений, поиска соответствий и нахождения трехмерных координат для неоткалиброванной пары изображений.
Постановка задачи. По двум изображениям одного объекта, снятых с разных ракурсов, требуется построить карту смещений для последующего восстановления глубины и 3D реконструкции. При этом считается, что параметры камеры являются неизвестными. Для решения данной задачи предлагается следующий алгоритм:
– Определение особых точек и сопоставление изображений;
– Вычисление фундаментальной матрицы;
– Ректификация изображений;
– Построение карты смещений.
Реализация алгоритма. Основой для расчета карты смещений является метод ограничения пространства поиска для нахождения соответствующих точек в эпиполярной плоскости между левым и правым изображениями. Эпиполярная плоскость — это плоскость, образованная точкой на сцене и оптическими центрами левой и правой камер. В пересечении эпиполярной плоскости и плоскости изображения формируется эпиполярная линия. Это линия, которая соединяет точки изображения с эпиполью. Эпиполи — это точки, где линия между двумя оптическими центрами пересекает плоскость изображения (см. рис. 1).
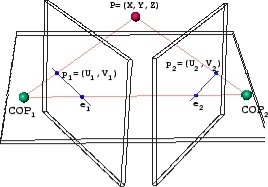
Рис. 1. Эпиполярная геометрия
Известно, что каждой точке на изображении одной камеры соответствует эпиполярная линия на изображении второй камеры и пара для точки обязательно лежит на этой эпиполярной линии. В случае, когда изображения откалиброваны, эпиполярные линии располагаются горизонтально и параллельно друг другу (такие изображения называют ректифицированными). Поэтому поиск парных точек для построения карты смещений осуществляется по одной горизонтали.
Чтобы найти соответствующие точки для построения карты смещений в данной задаче, необходимо каким-то образом ректифицировать изображения. Так как известно, что две камеры смотрят одну и ту же сцену, можно предположить, что две точки p1 и p2 могут быть изменены матрицей параметров камеры K на две точки p∗1 и p∗2 (преобразование: p∗1=Kp1 и p∗2=Kp2). Поскольку уравнения работают для точек p∗1 и p∗2, мы можем утверждать, что (p∗1)TFp∗2=0, где F — фундаментальная матрица [1]. Данная матрица имеет размер 3х3 и определяется с точность до константы, поэтому восемь пар точек соответствия будет достаточно для определения всех коэффициентов матрицы. Далее с помощью ФМ можно определить эпиполярные линии: l2=Fp1 для точки p1, и l1=FTp2 для точки p2. Этот процесс определения фундаментальной матрицы с использованием набора известных соответствий известен как метод «слабой» калибровки.
Такой метод калибровки требует заранее известный набор соответствующих точек для нахождения фундаментальной матрицы. Для нахождения и сопоставления особых точек на изображениях был выбран алгоритм ORB (Oriented FAST and Rotated BRIEF) [2]. Этот алгоритм является модификацией детектора FAST и дескриптора BRIEF и эффективной альтернативой методам SIFT и SURF, которые являются запатентованными.
Как было сказано ранее, для определения фундаментальной матрицы необходимо как минимум восемь пар точек соответствия. Для вычисления фундаментальной матрицы предлагается использовать алгоритм RANSAC [3], который позволяет выбрасывать «недостоверные» точки, так как они приводят к существенным ошибкам в расчетах.
Для ректификации необходимо установить связь между фундаментальной матрицей и желаемым преобразованием одного изображения в другое. Такая связь существует, поскольку целью преобразования является отображение эпиполярных линий на линии развертки изображений, а фундаментальная матрица характеризует эпиполярные линии. В работе [4] представлены средства определения ректификационных гомографий из фундаментальной матрицы. Результатом работы являются выровненные изображения так, что все эпиполярные линии параллельны сторонам изображения (обычно горизонтальны).
Для построения карты смещений по паре изображений для каждой точки на одном изображении выполняется поиск парной ей точки на другом. По паре таких точек можно выполнить триангуляцию, то есть определить координаты прообраза уже в трехмерном пространстве. Зная эти координаты, глубина вычисляется как расстояние до плоскости камеры. Поиск парных точек теперь происходит на одной эпиполярной линии. Для каждого пикселя первого изображения с координатами (u1, v1) выполняется поиск пикселя на втором изображении, предполагая, что пиксель на втором изображении имеет координаты (u1−d, v1), где d — это несоответствие/смещение (disparity). Для поиска смещений рассматривался алгоритм Semi — Global Matching [5]. Алгоритм состоит из 3х шагов: вычисление попиксельной стоимости, суммирование попиксельных стоимостей и вычисление карт диспаратности. Преимущества этого подхода состоит в том, что он дает очень неплохие результаты с точки зрения качества и результат достигается за приемлемое время.
Результаты. Алгоритм был реализован на языке Python 3.6 с использованием библиотеки OpenCV. Ниже приведены исходная пара изображений (см. рис. 2) и результат работы алгоритма — карта смещений (см. рис. 3).

Рис. 2. Исходная пара изображений
Визуально оценивая получившуюся карту диспаратности, можно сказать, что она подойдет для дальнейшего 3D моделирования.
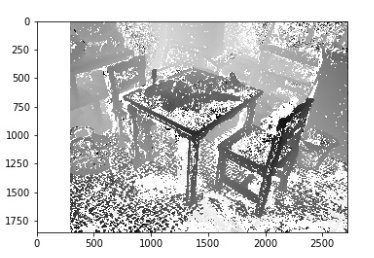
Рис. 3. Карта диспаратности.
Литература:
- Hartley R. I., Zisserman A. Multiple View Geometry in Computer Vision. Second Edition. Cambridge, UK: Cambridge University Press, 2004. 655 с.
- Rublee E., Rabaud V., Konolige K., Bradski G. ORB: An efficient alternative to SIFT or SURF // International Conference on Computer Vision. 2011. С.2564–2571.
- Fischler M., Bolles R. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography // Comm. of the ACM. 1981. No 24. С. 381–395.
- Loop C., Zhang Z. Computing rectifying homographies for stereovision // Computer Vision and Pattern Recognition. 1999. С.125–131.
- Hirschmuller H. Accurate and Efficient Stereo Processing by Semi-Global Matching and Mutual Information // Computer Vision and Pattern Recognition. 2005. No 2. С.807–814.







