Выбор стратегического решения с учетом субъективности оценки и компетентности эксперта



В статье представлена модификация нечёткого метода анализа иерархий, которая является инструментом экспертной оценки при выборе оптимального решения из возможных вариантов. Представленная модификация позволяет учитывать субъективность выставления оценок экспертами и компетентность экспертов. Для этого в вычислениях используются нечеткие числа второго типа. При определении компетентность эксперта учитывается самооценка эксперта и общественная оценка эксперта.

Ключевые слова: нечёткий МАИ, нечёткая функция принадлежности, субъективность оценок экспертов, нечеткие числа второго типа.

Введение

На выбор решения из нескольких возможных вариантов влияет отношение эксперта к рассматриваемому вопросу и его компетентность. Разработанные методы выбора решения не учитывают указанные факторы или учитывают только один из них. Анализируя ранее предложенные способы решения проблемы, можно выделить несколько методов.

1. Использование самооценки компетентности эксперта [2] Экспертам предлагается оценить свою компетентность по предложенной шкале компетентности. Таким образом, при парном сравнении возможных вариантов решения учитывается самооценка эксперта. После этого используется стандартный МАИ для обработки данных. Такой подход частично решает проблему, так как не учитывает субъективность оценок эксперта, а самооценка эксперта не всегда является точной.
2. Использование нечетких методов анализа иерархии. При использовании нечеткого МАИ учитывается субъективность выставления оценки, но не учитывают компетентность экспертов.
3. Использование метода тестирования для определения компетенции эксперта. Вопросы теста касаются области, для экспертизы которой привлекается специалист. По количеству правильных ответов определяется вероятность правильного выставления оценки экспертом [1]. Как видим из вышесказанного, разработанные методы не решают проблему в полной мере.

Модификация нечеткого метода анализа иерархии сиспользованием нечёткой функции принадлежности

По нашему мнению, для выбора оптимального решения необходимо использовать нечеткий метод анализа иерархии с учетом компетентности эксперта. Компетентность складывается из самооценки и показателя общественного мнения об эксперте со стороны других экспертов. Показатель общественного мнения можно рассчитать, используя метод экспертных оценок [4]. После выставления самооценки и оценивания эксперта другими экспертами, компетентность рассчитывается как среднее арифметическое выставленных оценок.

Самооценка и показатель общественного мнения определяется по следующей шкале [2]:

0,1 — уровень компетенции респондента не позволяет сравнить объекты;

0,2 — респондент имеет интуитивное представление о связи между объектами;

0,4 — респондент может логически обосновать свое мнение о связи между объектами;

0,6 — респондент имеет практические или теоретические знания о связи между объектами;

0,8 — респондент имеет практические и теоретические знания о связи между объектами;

1 — респондент является экспертом в данном вопросе, имеет собственные разработки или публикации о связи между объектами.

0,3; 0, 5; 0,7, 0,9 — соответствующие промежуточные значения.

Оценку компетентности эксперта предлагаем рассматривать как функцию принадлежности оценки эксперта в нечетком числе. После этого, проводится размывание оценки эксперта и функции принадлежности параметра а. В этом случае получаем нечеткое число второго типа (рис 1.)

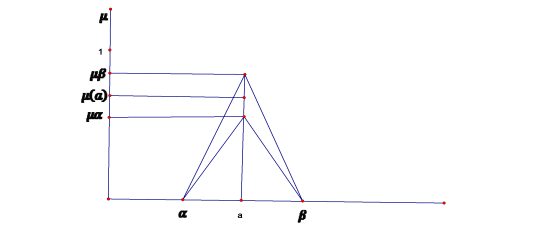
Рис. 1. Нечеткое число второго типа

Значение параметров и определяются следующим образом:

(1)

(2)

Определение.

Нечетким числом второго типа называется нечеткое подмножество универсального множества X, если значениями его функции принадлежности являются нечеткие подмножества интервала [0,1] [6].

Исследования показали [3], что при оперировании с нечеткими множествами второго типа можно использовать математику, разработанную для нечетких множеств первого типа, так как нечеткое число второго типа определено нижней функцией принадлежности LMF и верхней функцией принадлежности UMF, представляющие собой нечеткие числа (L — R) — типа.

Определение. Нечеткое число называется числом (L-R)-типа, если оно является нормальным унимодальным множеством, функция принадлежности, которой имеет вид:

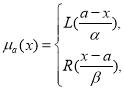
если

если (3)

где — параметры нечеткого числа [7].

В отличие от обычного нечеткого числа, в нечетких числах, рассматриваемые нами, параметр будет иметь значение функции принадлежности в интервале от 0 до 1 и обозначим

Введем арифметические действия для нечетких чисел и . Пустьи . Тогда

(5)

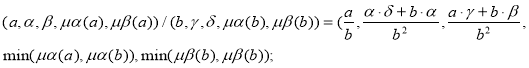(6)

где значения и можно вычислить по формуле:

.(7)

(8)

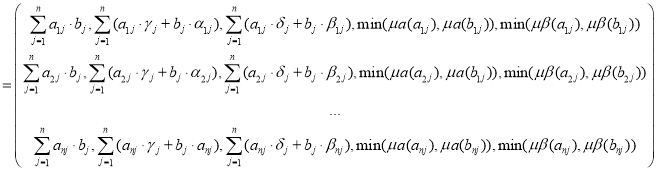
Дефазификацию будем выполнять по формуле:

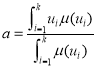р. (9)

Алгоритм метода следующий:

1. Определить цель

2. Создать многокритериальной модель проблемы в виде графа.

3. Построить матрицы сравнений между всеми критериями и альтернативами. Каждая оценка является нечетким числом, функция принадлежности задается степенью компетенции эксперта.

4. Преобразовать оценки экспертов и значения функции принадлежности нечетких чисел второго типа.

5. Вычислить построчные суммы нечетких чисел по формуле:

(10)

6. Вычислить сумму построчных сумм нечетких чисел:

. (11)

7. Нормализованные построчные суммы вычисляются так:

.(12)

8. Вычислить общий вектор приоритетов по формуле:

(13)

где — общий вектор приоритетов, — матрица нормализованных компонентов собственных векторов альтернатив, — собственный вектор критериев.

Наибольшее значение компонента общего вектора указывает на оптимальный выбор.

Пример.

Предприятиюнеобходимо заключить договор на обеспечение строительными материалами. Для этого нужно выбрать одного поставщика. Эксперты, используя стандартный МАИ, составили матрицу парных сравнений критериев и матрицы парных сравнений альтернатив. Оценка компетентности эксперта являет функцией принадлежности оценки эксперта.

Построим многокритериальную модель в виде графа (рис.2)

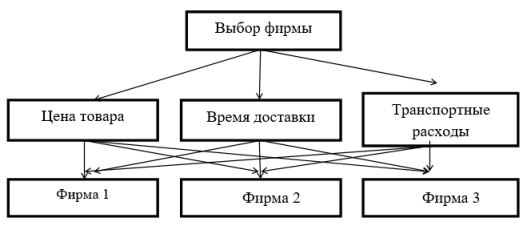
Рис. 2. Многокритериальная модель

Предположим, имеется матрица парных сравнений критериев, указанных в таблице 1.

Таблица 1

Матрица парных сравнений критериев

	Цена товара		Время доставки		Транспортные расходы
	оценка	μ(a)	оценка	μ(a)	оценка	μ(a)
Цена товара	1	1	0,33	0,8	4	1
Время доставки	3	0,8	1	1	0,25	1
Транспортные расходы	0,25	1	4	1	1	1

Преобразуем оценки экспертов и значения функции принадлежности в нечеткие числа второго типа, вычислим построчные суммы нечетких чисел и сумму построчных сумм нечетких чисел, вычислим вектор приоритетов и составим таблицы 2, 3.

Таблица 2

Таблица нечетких чисел парных сравнений критериев

	Цена товара					Время доставки					Транспортные расходы
	оценка					оценка					Оценка
		α	β	μα	μβ		α	β	μα	μβ		α	β	μα	μβ
Цена товара	1	0	0	1	1	0,33	0,066	0,066	0,7	0,9	4	0	0	1	1
Время доставки	3	0,6	0,6	0,7	0,9	1	0	0	1	1	0,25	0	0	1	1
Транспортные	0,25	0	0	1	1	4	0	0	1	1	1	0	0	1	1
расходы

Таблица 3

Построчные суммы ивектор приоритетов критериев

Построчные суммы					Вектор приоритетов
оценка					оценка
	α	β	μα	μβ		α	β	μα	μβ
5,33	0,066	0,066	0,7	0,9	0,359407	0,020591	0,020591	0,7	0,9
4,25	0,6	0,6	0,7	0,9	0,286581	0,053329	0,053329	0,7	0,9
5,25	0	0	1	1	0,354012	0,015898	0,015898	0,7	0,9
14,8	0,666	0,666	0,7	0,9

Предположим, имеется матрица парных сравнений по первому критерию, указанных в таблице 4.

Таблица 4

Матрица парных сравнений по первому критерию

	Фирма 1		Фирма 2		Фирма 3
	оценка	μ(a)	оценка	μ(a)	оценка	μ(a)
Фирма 1	1	1	3	1	4	0,7
Фирма 2	0,3	1	1	1	5	1
Фирма 3	0,25	0,7	0,2	1	1	1

Преобразуем оценки экспертов и значения функции принадлежности в треугольные нечеткие числа, вычислим построчные суммы нечетких чисел и сумму построчных сумм нечетких чисел по первому критерию и составим таблицы 5,6.

Таблица 5

Таблица нечетких чисел парных сравнений по первому критерию

	Цена товара					Время доставки					Транспортные расходы
	оценка					оценка					Оценка
		α	β	μα	μβ		α	β	μα	μβ		α	β	μα	μβ
Цена товара	1	0	0	1	1	3	0	0	1	1	4	1,2	1,2	1	1
Время доставки	0,3	0	0	1	1	1	0	0	1	1	5	0	0	1	1
Транспортные расходы	0,25	0,08	0,1	0,55	0,85	0,2	0	0	1	1	1	0	0	1	1

Таблица 6

Построчные суммы ивектор приоритетов по первому критерию

построчные суммы					вектор приоритетов
оценка					оценка
	α	β	Μα	μβ		α	β	μα	μβ
8	1,2	1,2	0,55	0,85	0,507937	0,1173091	0,117309	0,55	0,85
6,3	0	0	1	1	0,4	0,032381	0,017964	0,7	0,9
1,45	0,075	0,075	0,55	0,85	0,097775	0,0094483	0,009448	0,55	0,85
15,8	1,275	1,275	0,55	0,85

Предположим, имеется матрица парных сравнений по второму критерию. Значения указаны в таблице 7.

Таблица 7

Матрица парных сравнений по второму критерию

	Фирма 1		Фирма 2		Фирма 3
	оценка	μ(a)	оценка	μ(a)	оценка	μ(a)
Фирма 1	1	1	3	0,8	0,25	1
Фирма 2	0,3	0,8	1	1	4	1
Фирма 3	4	1	0,25	1	1	1

Преобразуем оценки экспертов и значения функции принадлежности в нечеткие числа, вычислим построчные суммы нечетких чисел и сумму построчных сумм нечетких чисел, вычислим вектор приоритетов, составим таблицы 8, 9.

Таблица 8

Таблица нечетких чисел парных сравнений по второму критерию

	Цена товара					Время доставки						Транспортные расходы
	оценка					оценка						оценка
		α	β	μα	μβ		α	β		μα	μβ			α	β		μα		μβ
Цена товара	1	0	0	1	1	3	0,6	0,6		0,7	0,9		0,25	0	0		1		1
Время доставки	0,3	0,06	0,1	0,7	0,9	1	0	0		1	1		4	0	0		1		1
Транспортные расходы	4	0	0	1	1	0,25	0	0		1	1		1	0	0		1		1

Таблица 9

Построчные суммы ивектор приоритетов по второму критерию

построчные суммы					вектор приоритетов
оценка					Оценка
	α	β	μα	μβ		α	Β	μα	Μβ
4,25	0,6	0,6	0,7	0,9	0,2871622	0,05334642	0,0533464	0,7	0,9
5,3	0,06	0,06	0,7	0,9	0,3581081	0,02003196	0,0201363	0,7	0,9
5,25	0	0	1	1	0,3540121	0,01589832	0,0158983	0,7	0,9
14,8	0,66	0,66	0,7	0,9

Предположим, имеется матрица парных сравнений по третьему критерию. Оценки экспертов указаны в таблице 10.

Таблица 10

Матрица парных сравнений по третьему критерию

	Фирма 1		Фирма 2		Фирма 3
	оценка	μ(a)	оценка	μ(a)	оценка	μ(a)
Фирма 1	1	1	0,3	0,8	4	0,5
Фирма 2	3	0,8	1	1	0,25	1
Фирма 3	0,25	0,5	4	1	1	1

Преобразуем оценки экспертов и значения функции принадлежности в нечеткие числа, вычислим построчные суммы нечетких чисел и сумму построчных сумм нечетких чисел, построим таблицы 11, 12.

Таблица 11

Таблица нечетких чисел парных сравнений по третьему критерию

	Цена товара							Время доставки							Транспортные расходы
	оценка							оценка							оценка
		Α	β	μα		μβ			α	β	μα		μβ			α	β	Μα		μβ
Цена товара	1	0	0	1		1	0,3		0,06	0,06	0,7		0,9	4		2	2	0,25		0,75
Время доставки	3	0,6	0,6	0,7		0,9	1		0	0	1		1	0,25		0	0	1		1
Транспортные расходы	0,25	0,13	0,13	0,25		0,75	4		0	0	1		1	1		0	0	1		1

Таблица 12

Построчные суммы ивектор приоритетов по третьему критерию

построчные суммы					вектор приоритетов
Оценка					Оценка
	α	β	μα	μβ		α	β	μα	μβ
5,3	2,06	2,06	0,25	0,75	0,3581081	0,20657642	0,2065764	0,25	0,75
4,25	0,6	0,6	0,7	0,9	0,2871622	0,09465965	0,0534367	0,7	0,9
5,25	0,125	0,125	0,25	0,75	0,3540121	0,02432718	0,0243272	0,25	0,75
14,8	2,785	2,785	0,25	0,75

Вычислим общий вектор приоритетов, составим таблицу 13

Таблица 13

Общий вектор приоритетов

вектор приоритетов
Оценка
	α	β	μα	Μβ
0,39	0,162047	0,1100748	0,25	0,75
0,35	0,082789	0,0443535	0,7	0,9
0,26	0,043085	0,027595	0,25	0,75

Определяем компоненты общего вектора в целых числах, составим таблицу 14.

Таблица 14

Компоненты общего вектора вцелых числах

Фирма 1	0,39162565
Фирма 2	0,3480486
Фирма 3	0,26191874

Анализируя полученные данные, видно, с учетом компетентности эксперта приоритетной является фирма 1.

Заключение

Стоит отметить, что представленная модификация МАИ позволяет обосновывать выбор варианта решения поставленной задачи с привлечением экспертов разного уровня подготовки и специальностей. Это стало возможным благодаря использованию нечеткого числа второго типа.

В качестве входных данных могут использоваться лингвистические высказывания экспертов и переводиться в числовые данные с помощью таблицы, предложенной Саати. Для расчета показателя общественного мнения можно использовать и другие методы.

Литература:

1. Бокова, О. В. Учет компетентности экспертов при оценке вероятности принятия ими верного управленческого решения в случае двух альтернатив // «Academy». 2016. С. 67–68
2. Луговой, Р. А. Инновационный подход к процессу стратегического управления ВУЗом на основе системы сбалансированных показателей [Текст]: дис. канд. эконом. наук: 08.00.05// Р. А. Луговой — Владивосток, 2006–167 с.
3. Ремезова Е. М. Модели поддержки принятия решения при подготовке проекта внедрения КИС на основе многоагентных систем и аппарата нечетких множеств [Текст]: автореф. дис. … канд. экон. наук: 08.00.13// Е. М. Ремезова. — С-Пб.: — 2017–17 с.
4. Попов, А. М. Экономико-математические методы и модели [Текст]: учебник для прикладного бакалавриата // А. М. Попов, В. Н. Сотников — 3-е изд. — М.: Издательство Юрайт, 2015. — 345 с.
5. Саати, Т. Л. Принятие решений. Метод анализа иерархий [Текст]// Т. Л. Саати — М.: Радио и связь, 1993.
6. Полещук, О. М. Определение взвешенных отрезков для специального класса интервальных нечетких чисел второго типа и операции с ними// «Лесной вестник». 2013 № 2 С. 147–150.
7. Конышева, Л. К. Основы теории нечетких множеств: Учебное пособие/ Л. К. Конышева, Д. М. Назарова — СПб.: Питер, 2011. — С.73.