Изучению динамических процессов, связанных с финансовыми и экономическими показателями, посвящено большое количество современной аналитической литературы. Нестабильность мировой экономики приводит к неугасающему интересу к способам прогнозирования валютных рисков и возможностям их снижения. Проблематика возникла из практических задач финансового анализа и управления рисками. К классу таких процессов относится и динамика курсов валют, требующая дополнительной оценки связанных с ней рисков. Поэтому актуальность данной темы, безусловно, не вызывает вопросов.
Одним из самых распространённых методов оценки риска является метод Value-at-Risk (VaR, Стоимость под риском), разработанный В 1980 году компанией J. P. Morgan. Этот метод позволяет определить максимальные возможные убытки, с заданной вероятностью. По сути, величина VaR является статистической оценкой, выраженной в денежных единицах.
Дельта-нормальный метод
Для вычисления VaR чаще всего используют дельта-нормальный метод. Его широкое использование связано с тем, что он прост в использовании, а точность расчета оказывается на высоком уровне.
Дельта-нормальный метод базируется на предположении о нормальном распределении изменения роста курса валют.
Логарифм изменения курса в момент t рассчитывается как:
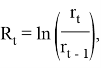
![]()
![]() — курс валюты в момент t;
— курс валюты в момент t;
![]() — курс валюты в предыдущий момент времени.
— курс валюты в предыдущий момент времени.
Формула расчета VaR:
![]()
– ![]() — квантиль нормального распределения для выбранного доверительного уровня.;
— квантиль нормального распределения для выбранного доверительного уровня.;
– ![]() — текущая стоимость открытой позиции;
— текущая стоимость открытой позиции;
– ![]() — волатильность курса валюты (среднеквадратичное отклонение);
— волатильность курса валюты (среднеквадратичное отклонение);
– ![]() — математическое ожидание изменений курса;
— математическое ожидание изменений курса;
Величина VaR с временным горизонтом T дней может быть рассчитана следующим образом:
![]()
Недостатком метода является то, что не всегда изменения валютного курса подчиняются нормальному закону распределения, соответственно во время нестабильности рынка оценка будет не точной.
Метод исторического моделирования
Не требует допущений о распределениях в отличие от дельно-нормального метода и полностью непараметрический. Однако для получения точных результатов, необходимы исторические данные достаточно больших объемов.
Алгоритм подсчета VaR методом исторического моделирования:
-
Выбирается глубина исторических данных
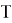 изменения курса валют;
изменения курса валют;
-
Затем полученные
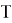 значений изменений курса валют ранжируются по убыванию, которые можно пронумеровать от 1 до
значений изменений курса валют ранжируются по убыванию, которые можно пронумеровать от 1 до 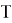 ;
;
-
После чего величина
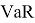 , в зависимости от заданного доверительного интервала
, в зависимости от заданного доверительного интервала 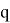 , равна величине изменения курса с номером, равным целой части числа
, равна величине изменения курса с номером, равным целой части числа 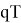 ;
;
Главным недостатком метода является полная зависимость от ретроспективных данных и от их особенностей. Мы допускаем, что прошлое, которое охватывают ретроспективный набор данных, — это надежное представление будущего. Это предполагает, что события, соответствующие ретроспективным данным, снова произойдут. Однако некоторые события исторического периода могут не повторятся в будущем.
Авторегрессионные модели условной гетероскедастичности
Финансовые ряды изменения курса валют обладают такими свойствами как:
– Гетероскедастичность — неоднородность наблюдений, выраженной в непостоянной дисперсии случайной ошибки модели регрессии.
– Кластеризация волатильности,котораяпоказывает, что финансовый показатель ведет себя либо непостоянно, либо относительно спокойно. То есть за промежутком времени с низкой волатильностью следует промежуток с низкой волатильностью, а за промежутком с высокой волатильностью, следует — идентичный.
В 1982 году Энгл [1] создал модель условной гетероскедастичности (ARCH), которая предназначена для моделирования этих свойств. Она представляет условную дисперсию как линейную функцию квадратов прошлых возмущений.
Модель ARCH порядка q, задается следующими соотношениями:
![]()
![]()
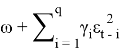
– ω — коэффициент, показывающий базовый уровень волатильности;
– ![]() случайные возмущения в прошлом;
случайные возмущения в прошлом;
– ![]() коэффициент, отвечающий за реакцию текущего значения волатильности на предыдущее изменение.
коэффициент, отвечающий за реакцию текущего значения волатильности на предыдущее изменение.
Для сохранения положительности условной дисперсии, необходимо
выполнение ограничений на коэффициенты
![]() .
.
Модели класса ARCH хорошо описывают кластеризацию волатильности, поскольку, исходя из их структуры, чем больше (или меньше) предыдущее значение волатильности, тем больше (меньше) его текущее значение.
Однако у них есть и существенные недостатки: они медленно реагируют на «выбросы” и требуют большого порядка для описания процесса, и, как следствие, определения большого количества параметров.
Рассмотрим усовершенствованную модель авторегрессионой условной гетероскедастичности введенную Бореслевом в 1986 году [2] — модель GARCH (обобщенная модель). Её преимуществом является моделирование процесса при меньшем числе параметров. Она усовершенствуется путем предположения о том, что условная дисперсия зависит также от её прошлых значений, а не только от квадратов прошлых значений временного ряда, как это было в ARCH.
Модель GARCH(1, 1):
– ![]() значение условной дисперсии в прошлом
значение условной дисперсии в прошлом
– ![]() -коэффициент — отвечает за сохранение эффекта высокой (низкой) волатильности.
-коэффициент — отвечает за сохранение эффекта высокой (низкой) волатильности.
Модель порядка p, q GARCH(p, q):
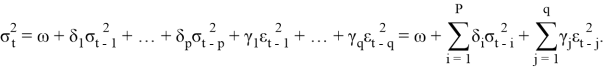
Также вводятся ограничения ![]() .
.
Ещё одним преимуществом GARCH-моделей является её свойство быстрого реагирования на различные изменения и такого же быстрого восстановления после сильных колебаний.
Стандартным методом для нахождения параметров модели GARCH является метод максимального правдоподобия (ММП).:
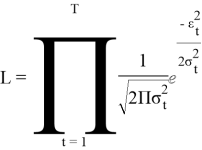
Для нахождения оценки ММП необходимо максимизировать функцию правдоподобия по неизвестным параметрам.
Существующих различных модификаций GARCH-моделей насчитывается уже более 300.
Например, существуют модели, которые отражают асимметричность дисперсии, то есть факт того, что отрицательный выброс приводит к более высокой условной дисперсии, чем положительный.
Пороговая модель(TGARCH) [3]:
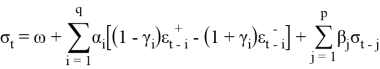
Или экспоненциальная модель (EGARCH(q, p)):
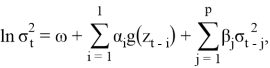
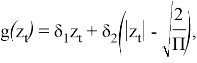
![]()
Которая также задает условную дисперсию в логарифмической форме, что означает, что нет необходимости вводить ограничение оценки для положительности дисперсии.
Однако, в 2004 году в исследовании Hansen, Lunde [4] был получен вывод о том, что стандартная модель GARCH(1,1) не сильно уступает различным лучшим модификациям авторегрессионных моделей.
Поэтому представленная здесь оценка VaR будет строиться на стандартной модели.
Суть расчета VaR с помощью модели GARCH(1,1) заключается в том что, используемый при расчете характеристики стоимости под риском стандартный показатель риска (выборочное среднеквадратическое отклонение), заменяется на условное среднеквадратическое отклонение рассчитываемое в рамках GARCH-модели.
Результаты
На графике (Рис. 1) приведены результаты реализации методов по оценки валютного риска путем расчета характеристики Value-at-Risk за период с января 2018 года по февраль 2019, с заданным доверительным интервалом 99 %.
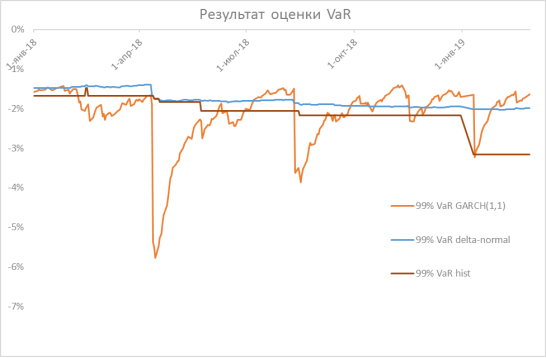
Рис. 1. Результаты реализации методов
Полученные значения VaR моделью GARCH(1,1) в периоды сильной волатильности заметно превышают по модулю значения, рассчитанные дельта-нормальным методом и методом исторического моделирования. В данном случае, можно сделать вывод, что стандартная обобщенная авторегрессионная модель условной гетероскедастичности показывает более реальную картину возможных потенциальных убытков.
Литература:
- Engle, RF. Autoregressive conditional heteroskedasticity with estimates of the variance of U. K. inflation. // Econometrica 45: 987– 1007, 1982.
- Bollerslev, T. Generalized autoregressive heteroskedasticity. // Journal of Econometrics 31: 307– 327, 1986
- Nelson, D. Conditional Heteroskedasticity in Asset Returns: A New Approach. // Econometrica, 59, 347–370, 1991.
- Peter R. Hansen, Asger Lunde. A comparison of volatility models: Does anything beat a GARCH(1,1), 2004.







