Ключевые слова: математическое моделирование, модель Ховорки, обратная связь, инсулин, глюкоза.
Сахарный диабет является глобальной медико-социальной проблемой уже на протяжении нескольких десятилетий, в связи с этим математические модели широко используются в исследованиях для контроля уровня глюкозы в крови. Целью такого рода моделирования является реализация непрерывного мониторинга глюкозы в режиме реального времени посредством автоматической внутривенной инфузии инсулина пациентам. При достаточно точной математической модели пациента может быть назначена правильная дозировка и частота введения инсулина.
В данной работе рассмотрена модель Ховорки, которая демонстрирует модель для пациента с диабетом 1-го типа. Это заболевание характеризуется абсолютной недостаточностью инсулина. Основным диагностическим признаком диабета является хроническая гипергликемия — повышенный уровень сахара в крови.
Описание математической модели
Модель Ховорки — это нелинейная модель, состоящая из подсистемы глюкозы (абсорбция, распределение и вывод), инсулиновой подсистемы (абсорбция, распределение и разрушение инсулина) и подсистемы действия инсулина [1].
a) Подсистема глюкозы
Подсистема глюкозы разделена на два отделения: масса глюкозы в доступной камере и масса глюкозы в недоступной камере.
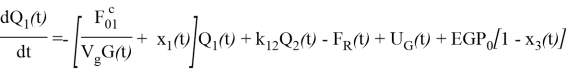
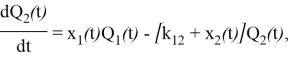
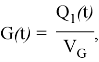
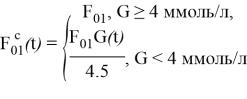
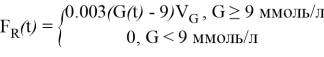
где 
и 
— массы глюкозы в доступных (в которых проводятся измерения, т. е. в крови) и недоступных (в периферических тканях) камерах, соответственно. 
— это константа скорости передачи из недоступной в доступную камеру. 
— объем распространения доступного отделения. 
— концентрация глюкозы в плазме. 
— скорость абсорбции в кишечнике. 
–эндогенная продукция глюкозы, экстраполированная до нулевой концентрации инсулина. 
— суммарный инсулиннезависимый уровень глюкозы. 
— почечный клиренс глюкозы выше порога глюкозы в 162 мг/дл.
b) Подсистема инсулина
Абсорбция инсулина:
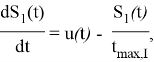
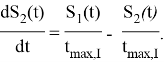
Параметры 
— абсорбция вводимого инсулина в двух камерах, 
— время максимального поглощения подкожно введенного инсулина. Концентрация инсулина в плазме 
описывается следующим уравнением:
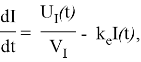
где 
— коэффициент частичной элиминации (выведения из организма), а 
— объем распределения, 
— скорость поглощения инсулина.
c) Подсистема действия инсулина
Концентрация инсулина в плазме оказывает влияние на транспорт глюкозы из плазмы в ткани, выработку глюкозы в печени и утилизацию периферической глюкозы. Эти действия моделируются следующим образом:
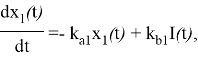
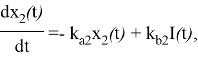
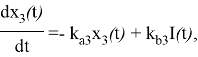
где 
— влияние инсулина на распределение/перенос глюкозы, удаление глюкозы и выработку эндогенной глюкозы, соответственно; 
— константы скорости дезактивации; 
являются константами активации.
Численное моделирование
Параметры: 
(ммоль/(кг*мин)), 
(ммоль/(кг*мин)).
Константы модели [1]:
|
Параметр |
Значение |
Размерность |
|
|
|
1/мин |
|
|
|
1/мин |
|
|
|
1/мин |
|
|
|
л/(мЕд*мин) |
|
|
|
л/(мЕд*мин) |
|
|
|
л/(мЕд*мин) |
|
|
|
1/мин |
|
|
|
л |
|
|
|
л |
|
|
|
мин |
Результаты численного моделирования модели Ховорки без использования обратной связи продемонстрированы на рисунке 1. На первом графике иллюстрируется непрерывная подача инсулина пациенту, равная 3 мЕд/мин. Динамика глюкозы показана на втором графике относительно своих предельных и нормальных значений. Наблюдается резкое возрастание концентрации глюкозы в крови после приемов пищи, полученные значения выходят за допустимые верхние и нижние пределы. Основной задачей последующего внедрения PID-регулятора [2] является нормализация концентрации в границах допустимых значений.
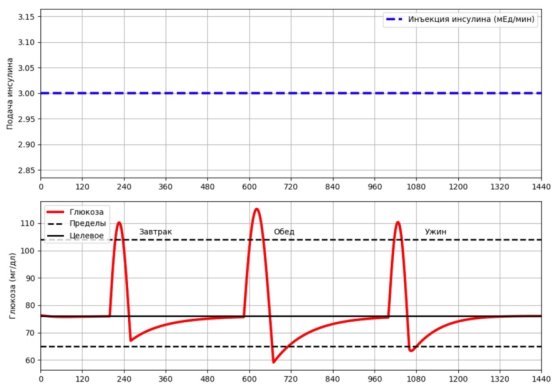
Рис. 1. Результаты численного моделирования динамики глюкозы без использования обратной связи
Используем механизм обратной связи в виде PID-контроллера с параметрами: 
, 
. Полученный результат можно видеть на рисунке 2. С помощью регулировки параметров контроллера получено нужное решение поставленной задачи, то есть минимизированы выходы показателей концентрации глюкозы за допустимые значения. Максимальное увеличение инфузии инсулина составляет от 3,5 до 8 мЕд/мин. Благодаря корректному введению инсулина значительно уменьшается риск наступления гипо- и гипергликемии.
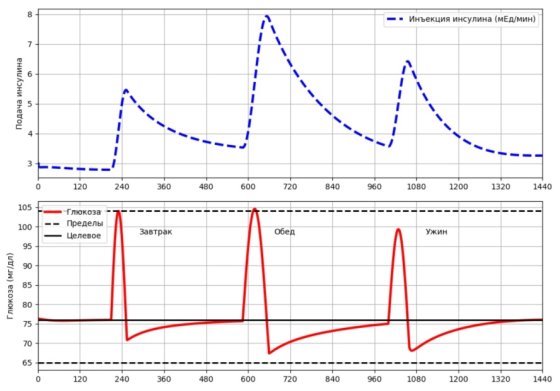
Рис. 2. Результаты численного моделирования динамики глюкозы с использованием механизма обратной связи
Заключение
В ходе исследования проанализирована математическая модель Ховорки динамики уровня глюкозы в крови и инсулина при заболевании диабетом 1-го типа. Для имитационного моделирования приема пищи и инфузии инсулина была разработана программа на языке Python, рассмотрены различные сценарии поведения системы в зависимости от входных параметров. Учтен непрерывный контроль уровня глюкозы в крови у больных диабетом с помощью механизма обратной связи, а именно PID-контроллера. Полученные численные результаты соответствуют известным опубликованным данным и дают возможность для построения математических моделей, которые учитывают еще более сложные процессы в организме.
Литература:
- Roman Hovorka, Valentina Canonico, Ludovic J Chassin, Ulrich Haueter, Massimo Massi-Benedetti, Marco Orsini Federici, Thomas R Pieber, Helga C Schaller, Lukas Schaupp, Thomas Vering and Malgorzata E Wilinska. Nonlinear model predictive control of glucose concentration in subjects with type 1 diabetes // Physiological Measurement. — 2004. — № 25. — P. 905–920.
- Dynamics and Control. Proportional Integral Derivative (PID) Control. http://apmonitor.com/pdc/index.php/Main/ProportionalIntegralDerivative
