Ключевые слова: прогноз, инфляции, сезонная модель ARIMA, гребневая регрессия, лассо регрессия.
Монетарное регулирование экономики есть неотъемлемый элемент макроэкономической политики государства. В 2014 году Центральный Банк Российской Федерации перешел на инфляционное таргетирование, обеспечивая при этом ценовую стабильность. По согласованию с Правительством РФ Банк России установил среднесрочную цель по инфляции на уровне 4 % в год [1].
Учитывая вышесказанное, важность прогнозирования уровня инфляции очевидна. Практически каждый гражданин РФ обращает на нее внимание и задается вопросом о том, когда цены вырастут и насколько. Домохозяйствам и предприятиям нужны оценки будущих цен для принятия взвешенных и обоснованных решений. Политики, чья работа заключается в оказании помощи в принятии этих решений путем поддержания стабильных цен, нуждаются в точных прогнозах, чтобы отслеживать инфляцию и вносить коррективы в курс при необходимости. Кроме того, центральные банки полагаются на прогнозы инфляции не только для информирования денежно-кредитной политики, но и для закрепления инфляционных ожиданий и, следовательно, повышения эффективности политики. Действительно, с целью улучшения процесса принятия экономических решений многие центральные банки регулярно публикуют сведения о прогнозе инфляции.
В данной работе будут рассмотрены методы предсказания, использующие модель ARIMA, а также построенные на основе гребневой регрессии.
Для измерения уровня инфляции выбран индекс потребительских цен. В России при расчете данного индекса используется потребительская корзина, содержимое которой утверждается Федеральным законом № 44-ФЗ «О потребительской корзине в целом по Российской Федерации». В нее входят как продовольственные и непродовольственные товары, так и услуги различного рода.
Данные
В данной работе использована официальная статистика об уровне цен, публикуемая Росстатом [2]. Действуя согласно теории статистики, для получения ИПЦ за определенный период требуется перемножить все входящие в этот временной промежуток индексы, объясняющие изменение цен в отчетном периоде по сравнению с предыдущим.
Здесь будет рассмотрена ежемесячная динамика инфляции в России за период с января 1999 года по март 2019 года (Рис. 1), рассчитанная на основе ИПЦ по формуле:
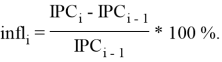
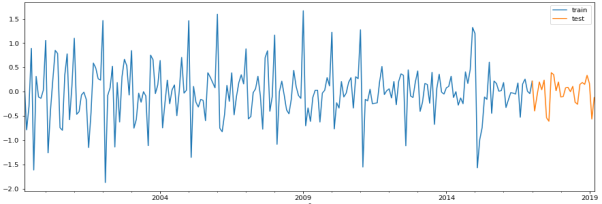
Рис.1. Динамика инфляции в России
Все данные разделены на две части (Рис. 1): тренировочную и тестовую. Тренировочная выборка нужна для обучения модели, тестовая — для проверки качества.
Перед непосредственным построением моделей проведена предобработка данных:
– Проверка на выбросы:
![]()
где ![]() — первая квартиль,
— первая квартиль, ![]() — третья квартиль;
— третья квартиль;
– Данные стандартизированы (![]() ).
).
Оценивание качества прогнозов производится с помощью среднеквадратичной ошибки, вычисляемой по формуле:
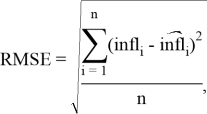
где ![]() — наблюдаемое значение инфляции,
— наблюдаемое значение инфляции, ![]() — построенное моделью.
— построенное моделью.
Сезонная ARIMA модель
Сезонная модель ARIMA (SARIMA) — это сезонная интегрированная модель авторегрессии — скользящего среднего [3], являющаяся расширением модели ARIMA на временные ряды с сезонностью, которая в свою очередь является обобщением модели ARMA.
С помощью лаговых операторов данная модель записывается следующим образом [3]:
![]()
где ![]() — порядок сезонной авторегрессии,
— порядок сезонной авторегрессии, ![]() — порядок интегрирования сезонной составляющей,
— порядок интегрирования сезонной составляющей, ![]() — порядок сезонной модели скользящего среднего,
— порядок сезонной модели скользящего среднего, ![]() — случайная ошибка,
— случайная ошибка, ![]() — порядок авторегрессии тренда,
— порядок авторегрессии тренда, ![]() — порядок интегрирования исходных данных,
— порядок интегрирования исходных данных, ![]() — порядок модели скользящего среднего,
— порядок модели скользящего среднего, ![]() — период временного ряда.
— период временного ряда.
Построение модели ![]() реализовано на языке Python в библиотеке Statsmodels.
реализовано на языке Python в библиотеке Statsmodels.
Гиперпараметры ![]() настраиваются путем поиска в сетке набора конфигураций параметров и определения того, какие комбинации работают лучше для данного одномерного временного ряда. В качестве меры качества используется информационный критерий Акаике (AIC). Получены следующие значения параметров:
настраиваются путем поиска в сетке набора конфигураций параметров и определения того, какие комбинации работают лучше для данного одномерного временного ряда. В качестве меры качества используется информационный критерий Акаике (AIC). Получены следующие значения параметров:
![]()
На графике (Рис. 2) показана реальная динамика инфляции (желтая линия) и предсказанные значения с помощью модели (голубая линия) на тестовой выборке.
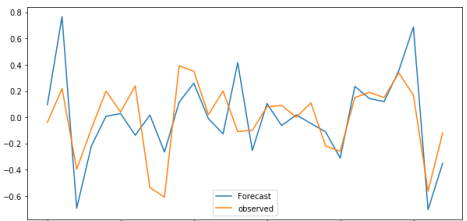
Рис. 2. Реальные и предсказанные значения моделью SARIMA
Гребневая регрессия
Гребневая регрессия (Ridge Regression) — это регрессионная модель с регуляризацией [4].
Модель гребневой регрессии (Ridge Regression) реализована на языке Python в библиотеке Scikit-learn. Прогнозирование осуществляется в режиме псевдореального времени на отложенных выборках со скользящим годовым окном (12 месячных значений).
Гиперпараметр данной модели найден на кросс-валидации (перекрестной проверке). Этот подход используется для анализа поведения модели на независимых данных. Получено: ![]() .
.
На графике (Рис. 3) построена динамика наблюдаемой инфляции (желтая линия) и предсказанной с помощью гребневой регрессии (голубая линяя).
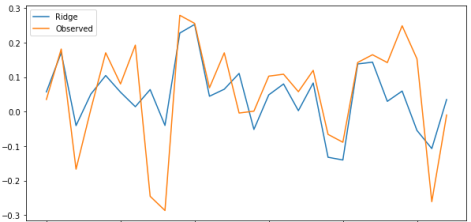
Рис. 3. Реальные и предсказанные значения Гребневой регрессией (Ridge)
Результаты
Модели показали следующие значения ошибки на тестовой выборке:
– Модель SARIMA: ![]() ;
;
– Гребневая регрессия:
На основании результатов анализа временного ряда инфляции и его прогнозирования можно сделать вывод, что прогноз, построенный с помощью гребневой регрессии, значительно точнее, чем прогноз, основанный на сезонной модели ARIMA. А, следовательно, гребневая регрессия с учетом всех достоинств и некоторых недостатков может и должны быть использована в прогнозировании динамики инфляции в России.
Литература:
- Основные направления единой государственной денежно-кредитной политики. http://www.cbr.ru/publ/ondkp/.
- Официальный сайт Центрального Банка России http://www.gks.ru/.
- P. Arumugam, R. Saranya Outlier Detection and Missing Value in Seasonal ARIMA Model Using Rainfall Data \\ Materials Today: Proceedings on ScienceDirect. 2018. Vol. 5. Issue 1. Part 1. P. 1791–1799.
- К. В. Воронцов Лекции по алгоритмам восстановления регрессии 2007.







