В статье рассмотрены методы решения нелинейных уравнений в Microsoft Excel и MathСad. Произведено сравнение удобства выполнения расчетов, выполнено сравнение функциональных возможностей этих программных продуктов.
При решении многих задач из областей химии, физики, экономики и др. требуется решить нелинейные уравнения, то есть найти их корни — точки, в которых уравнение обращается в верное тождество. Универсальных методов решения таких уравнений не существует.
Общий механизм решения сводится к приведению их к виду f(x)=0. Далее производится поиск приближенного решения с достаточной точностью
Для решения многих практических задач, в которых необходимо решить нелинейные уравнения, используется всевозможное программное обеспечение, например, Microsoft Excel, MathСad, SmathStudio.
Рассмотрим две наиболее популярные и удобные в использовании программы — Microsoft Excel и MathСad.
Microsoft Excel — программа для работы с электронными таблицами, созданная корпорацией Microsoft.
Приведем пример нахождения корней нелинейного уравнения в Microsoft Excel.
Выполним табулирование функции. На основе полученной таблицы табуляции строим график функции (рис.1).
На полученном графике определяем приближенные значения корней уравнения. Данные корни будут находиться в точках пересечения графика функции с осью абсцисс, а также их приближенные значения можно определить по таблице табуляции в строках, где значения в столбце y меняют свой знак. С помощью процедуры «Поиск решения» определяем точное значение корня для каждого приближенного значения (рис.2.). В качестве целевой функции указывается ячейка с формулой функции. Изменяются ячейки, которые выполняют роль аргумента функции, ограничения задаются, исходя из локализации корней.
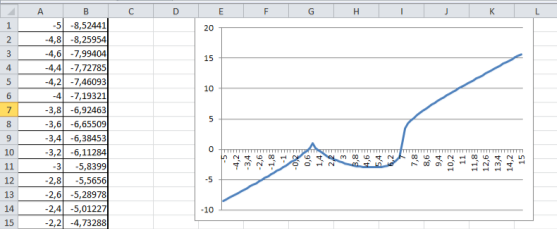
Рис. 1. Табуляция функции и построение графика в Excel
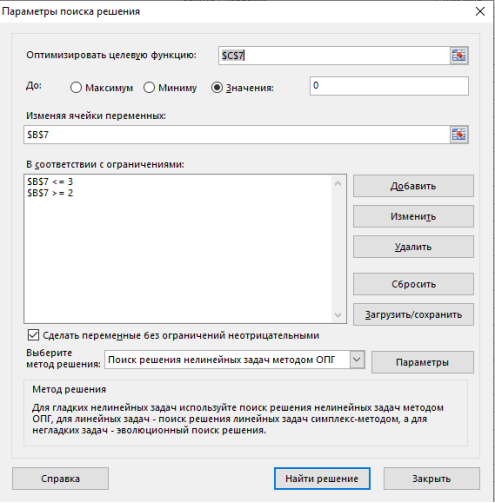
Рис. 2. Окно процедуры «Поиск решения» в Excel
Mathcad — программа для математических, инженерных вычислений, распространения и хранения расчетов, продукт компании PTC. Является универсальной системой, т. е. может использоваться практически в любой области техники и науки — везде, где необходимы объёмные вычисления.
Приведем пример нахождения корней нелинейного уравнения в MathCad. С помощью программы Mathcad построим график функции. По графику определяем приближенные значения корней уравнения (рис.2.). С помощью функции root находим точные значения корней уравнения (рис.3.).
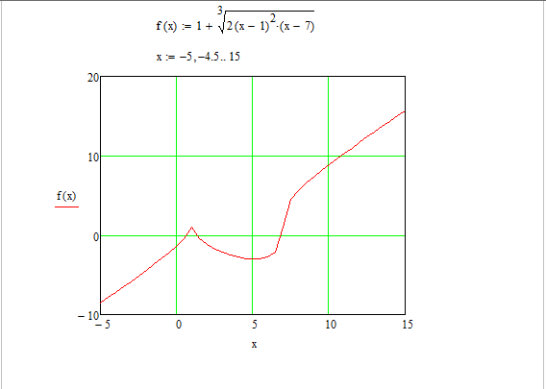
Рис. 3. Построение графика функции в Mathcad

Рис. 4. Нахождение корней уравнения в Mathcad
Мы рассмотрели две популярные программы для математического вычисления — Microsoft Excel и MathСad и их возможности для решения нелинейных уравнений.
Стоит отметить, что в статье рассмотрен лишь один, самый простой по мнению авторов, способ нахождения корней уравнений. Функционал обеих программ предусматривает и другие способы поиска решений.
Применение описанных программ позволяет сократить время на решение и исключить возможность вычислительных и алгоритмических ошибок.
В MathCad данная задача решается несколько быстрее, поскольку требует выполнения меньшего количества действий.
Результаты, полученные в обеих программах в целом совпадают, но могут отличаться на незначительную величину в связи с применением различных алгоритмов итерационных вычислений корней нелинейных уравнений. Полученные погрешности при решении практических задач оказываются вполне допустимыми и на них можно не обращать внимания.
Функционал Excel по сравнению с Excel, MathСad несколько менее приспособлен к решению подобного рода задач, однако программа имеет привычный интерфейс, удобный доступ к справочной информации и встроенные возможности исправления ошибок.
Из недостатков обеих программ можно отметить их относительно большую стоимость. Однако, Excel входит в стандартный пакет Microsoft Office, является более распространенным и привычным пользователю.
Литература:
- В. В. Штыков. MathCAD: руководство по решению задач для начинающих / — Москва: URSS, cop. 2016. — 163, [2] с.: ил.
- Долженков В. А. Самоучитель Excel — CПб.:БХВ-Петербург, 2018. — 400 с.: ил.
- Очков В. Ф. Mathcad для студентов, инженеров и конструкторов. — СПб.: БХВ-Петербург, 2017. — 368 с.: ил.
- Т. В. Зудилова, С. В. Одиночкина, И. С. Осетрова, Н. А. Осипов Работа пользователя в Microsoft Excel — СПб: НИУ ИТМО, 2019. — 87 с.







