Хорошо известно, что реализованная волатильность (далее — RV) является гораздо более информативной оценкой волатильности, чем возведение в квадрат [1–5]. Были предложены различные методы для включения RV в оценку и прогнозирование волатильности, в том числе модель GARCH-X [6], модель MEM [6], модель HEAVY [7], и самый последний RealGARCH [8]. Среди них модель RealGARCH является наиболее популярной, поскольку она обеспечивает основу для совместного моделирования доходности и реализованной волатильности.
В рамках RealGARCH были предложены различные варианты, например, линейный RealGARCH [8], лог-линейный RealGARCH [8], RealEGARCH [9] и самый последний CarrGARCH [10].
В данной работе проводится работа по сравнению трех последних, приведенных выше вариантов RealGARCH. Нет смысла исследовать линейный RealGARCH, так как в литературе доказано, что лог-линейный RealGARCH является более предпочтительным, чем линейный RealGARCH.
Варианты моделей. RealGARCH Framework — это совместное моделирование доходности и реализованной волатильности. Общая структура модели RealGARCH![]() определяется выражениями:
определяется выражениями:
![]() ,
,
![]() ,
,
![]() ,
,
где {![]() } — возвращаемый ряд,
} — возвращаемый ряд, ![]() — осознанная мера волатильности,
— осознанная мера волатильности, ![]() ,
, ![]() и
и ![]() взаимно независимы.
взаимно независимы.
Первые два уравнения называются уравнением возврата и уравнением GARCH, а последнее называется уравнением измерения. Различные спецификации для ![]() и
и ![]() дают разные варианты RealGARCH.
дают разные варианты RealGARCH.
В эмпирическом случае рассматриваются только варианты порядка![]() , так как доказано, что порядок
, так как доказано, что порядок ![]() достаточен для отражения динамики волатильности.
достаточен для отражения динамики волатильности.
Лог-линейный реализованный GARCH. RealGARCH с логарифмической спецификацией характеризуется [8]:
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ,
, ![]() — реализованная дисперсия,
— реализованная дисперсия, ![]() — функция плеча [8]. Лог-линейный RealGARCH включает эффект левереджа косвенно в уравнении GARCH через уравнение измерения.
— функция плеча [8]. Лог-линейный RealGARCH включает эффект левереджа косвенно в уравнении GARCH через уравнение измерения.
Реализованный EGARCH. Модель Realized Exponential GARCH (RealEGARCH), которая может использовать несколько реализованных показателей волатильности для моделирования возвращаемых серий представляется как [9]:
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() — функция плеча.
— функция плеча.
Основное различие между лог-линейным RealGARCH и RealEGARCH состоит в том, что RealEGARCH включает в себя новую функцию кредитного плеча ![]() в уравнении GARCH, что делает ее более гибкой в использовании эффекта кредитного плеча.
в уравнении GARCH, что делает ее более гибкой в использовании эффекта кредитного плеча.
CarrGARCH. Определяя MEM (модель мультипликативной ошибки) для уравнения измерения, предлагается следующий вариант [10]:
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ,
, ![]() логарифмически нормален со средним значением единицы. Масштабный коэффициент
логарифмически нормален со средним значением единицы. Масштабный коэффициент ![]() используется для того, чтобы убедиться, что
используется для того, чтобы убедиться, что ![]() является объективной оценкой волатильности. Поскольку два последних уравнения известны как модель условной авторегрессии реализованной волатильности, таким образом, этот вариант RealGARCH называется CarrGARCH. Квадратный корень реализованной дисперсии используется по той причине, что CarrGARCH предназначен для стандартного отклонения вместо дисперсии.
является объективной оценкой волатильности. Поскольку два последних уравнения известны как модель условной авторегрессии реализованной волатильности, таким образом, этот вариант RealGARCH называется CarrGARCH. Квадратный корень реализованной дисперсии используется по той причине, что CarrGARCH предназначен для стандартного отклонения вместо дисперсии.
Основное различие между CarrGARCH и двумя другими вариантами состоит в том, что модель CarrGARCH является ограниченным RealEGARCH. Стоит отметить, что ![]() ,
, ![]() . Последнее уравнение в CarrGARCH эквивалентно:
. Последнее уравнение в CarrGARCH эквивалентно:
![]() .
.
Из уравнений измерений моделей CarrGARCH и RealEGARCH получается:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Это ограничение делает модель CarrGARCH более лаконичной и более простой в своей спецификации, чем два других варианта.
Сравнивая три варианта RealGARCH, обнаружено, что наиболее существенным отличием является сложность спецификации модели. В лог-линейном RealGARCH есть 8 параметров — ({![]() }), 10 параметров в RealEGARCH ({
}), 10 параметров в RealEGARCH ({![]() }) и 7 параметров в CarrGARCH ({
}) и 7 параметров в CarrGARCH ({![]() }). Всесторонний анализ эффективности прогнозирования этих трех вариантов может помочь лучше понять, как сложность модели может повлиять на эффективность прогнозирования RealGRACH.
}). Всесторонний анализ эффективности прогнозирования этих трех вариантов может помочь лучше понять, как сложность модели может повлиять на эффективность прогнозирования RealGRACH.
Метод оценки. Тест Diebold-Mariano (далее DM) используется для сравнения двух конкурирующих моделей прогнозирования [11]. Пусть потери, о которых сообщают модели
![]() ,
,
где 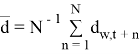 , а
, а ![]() — общее количество прогнозов.
— общее количество прогнозов.
Дисперсия ![]() ,
, ![]() находится оценкой согласованности гетероскедастичности и автокорреляции (HAC). DM показывает, что при нулевой гипотезе равной точности предсказания статистика DM следует стандартному нормальному распределению [11].
находится оценкой согласованности гетероскедастичности и автокорреляции (HAC). DM показывает, что при нулевой гипотезе равной точности предсказания статистика DM следует стандартному нормальному распределению [11].
Поскольку истинная волатильность скрыта, можно использовать прокси волатильности только как «истинную волатильность» для построения статистики DM. Было отмечено, что несовершенный показатель волатильности может исказить рейтинг конкурирующих прогнозов волатильности. Исследуя класс функций потерь можно обнаружить, что только MSE (среднеквадратическая ошибка) и QLIKE (функция потери квази-правдоподобия) устойчивы к несовершенному показателю изменчивости. Более того, установлено, что QLIKE менее чувствителен к экстремальным наблюдениям, чем квадрат потери ошибок. MSE и QLIKE определены как:
![]() ,
,
![]() ,
,
где ![]() и
и ![]() — потери для модели прогнозирования
— потери для модели прогнозирования ![]() .
.
В данной работе также используется линейный регрессионный анализ для оценки эффективности прогнозирования различных моделей:
![]() ,
, ![]() ,
,
где ![]() — прокси волатильности,
— прокси волатильности, ![]() — прогноз, сообщенный моделью
— прогноз, сообщенный моделью ![]() . Если модель
. Если модель ![]() сообщает о непредвзятой оценке волатильности, ожидается, что
сообщает о непредвзятой оценке волатильности, ожидается, что ![]() и
и ![]() .
.
Эмпирические результаты. Для эмпирического исследования используется набор данных, который включает биржевой индексный фонд SPY, который отслеживает индекс S&P500 и 10 отдельных акций. Поскольку ежедневные высокочастотные цены доступны только в периоды между «открытием» и «закрытием», используется возврат от закрытия к закрытию.
В данной работе оцениваются три варианта RealGARCH посредством прогнозирования вне выборки. Используется процедура прогнозирования рекурсивного (расширяющегося) окна, а последние 500 данных наблюдений используются для оценки. Реализованное ядро (RK) используется в качестве реализованной меры. Этот выбор основан на теоретических преимуществах меры RK: он устойчив к микроструктурированию шума, эффективно использует внутридневные данные, является одной из лучших оценок с точки зрения эффективности и устойчивости к изменяющимся во времени параметрам.
В Таблице 1 представлена статистика DM. Модель CarrGARCH используется в качестве эталона и сравнивается с лог-линейным RealGARCH и RealEGARCH, результаты представлены тестами «A» и «B». Взяв в качестве эталона лог-линейный RealGARCH, производится его сравнение с RealEAGRCH, результаты представлены тестом «C». Статистика DM рассчитывается по всем отдельным активам, а результаты отображаются в последней строке. Согласно средней статистике DM, видно, что в среднем CarrGARCH доминирует над двумя другими вариантами, а лог-линейный RealGARCH доминирует над RealEGARCH. Статистика DM теста «A» показывает, что CarrGARCH доминирует над лог-линейным RealGARCH в 3 (4) из 10 активов MSE (QLIKE). Доминирование CarrGARCH над RealEGARCH более существенно по статистике DM теста «B». В 4 (8) из 10 активов CarrGARCH доминирует над RealEGARCH по MSE (QLIKE). Лог-линейный RealGARCH доминирует в RealEGARCH в 0 (1) из 10 активов MSE (QLIKE).
Таблица 1
Оценка эффективности прогнозирования: тест DM
|
Тест CarrGARCH |
Тест лог-линейный RealGARCH |
|||||
|
A: Лог-линейный RealGARCH |
B: RealEGARCH |
C: RealEGARCH |
||||
|
MSE |
QLIKE |
MSE |
QLIKE |
MSE |
QLIKE |
|
|
SPY |
1.83 |
2.22* |
1.05 |
2.00* |
-0.61 |
-1.38 |
|
AA |
2.35* |
1.05 |
2.74* |
2.04* |
1.60 |
1.30 |
|
DD |
1.68 |
1.49 |
1.83 |
2.13* |
1.59 |
1.87 |
|
GE |
2.48* |
3.82* |
1.88 |
4.28* |
1.14 |
2.68* |
|
HD |
-0.62 |
0.04 |
2.82* |
2.42* |
1.30 |
0.78 |
|
IBM |
-0.76 |
0.22 |
0.19 |
2.25* |
-0.11 |
1.86 |
|
MMM |
-0.65 |
-0.23 |
1.57 |
-0.75 |
1.66 |
1.70 |
|
MRK |
1.12 |
2.13* |
1.13 |
2.01* |
-1.40 |
-1.57 |
|
PG |
1.52 |
-0.50 |
2.19* |
0.02 |
-1.32 |
0.99 |
|
XOM |
2.47* |
2.72* |
2.16* |
2.26* |
0.33 |
0.31 |
|
Среднее |
1.02 |
1.38 |
1.12 |
2.06 |
0.44 |
0.99 |
Примечание: t-статистика, превышающая 1,96 по абсолютной величине, указывает на отклонение на уровне 5 % (отмечены звездочкой). Положительный знак t-статистики указывает, что эталонная модель превосходит, а отрицательный знак указывает на обратное.
Принимая RK в качестве показателя волатильности, в Таблице 2 приведены результаты линейной регрессии. Рассчитывается средний перехват (а), средний наклон (b) и средний R-квадрат (![]() ), результаты представлены в последней строке. В соответствии со статистикой DM результаты показывают, что в среднем CarrGARCH сообщает о наименьших смещенных прогнозах вне выборки, тогда как RealEGARCH сообщает о наибольших смещенных прогнозах вне выборки.
), результаты представлены в последней строке. В соответствии со статистикой DM результаты показывают, что в среднем CarrGARCH сообщает о наименьших смещенных прогнозах вне выборки, тогда как RealEGARCH сообщает о наибольших смещенных прогнозах вне выборки.
Таблица 2
Оценка эффективности прогнозирования: линейная регрессия
|
A: CarrGARCH |
B: Лог-линейный RealGARCH |
C: RealEGARCH |
|||||||
|
a |
b |
|
a |
b |
|
a |
b |
|
|
|
SPY |
-0.01 |
0.94* |
0.59 |
0.04 |
0.90* |
0.55 |
-0.02 |
0.96* |
0.57 |
|
AA |
0.17 |
1.16* |
0.43 |
-0.13 |
1.29* |
0.40 |
0.14 |
1.20* |
0.41 |
|
DD |
0.14 |
1.36* |
0.49 |
-0.27* |
1.49* |
0.48 |
-0.30* |
1.53* |
0.46 |
|
GE |
0.03 |
1.11* |
0.51 |
0.13 |
1.04* |
0.48 |
0.06 |
1.13* |
0.49 |
|
HD |
-0.07 |
1.18* |
0.61 |
-0.02 |
1.16* |
0.62 |
-0.16 |
1.25* |
0.61 |
|
IBM |
0.09 |
1.09* |
0.49 |
0.21* |
0.95* |
0.46 |
0.16* |
1.01* |
0.48 |
|
MMM |
0.11 |
1.26* |
0.49 |
-0.06 |
1.21* |
0.48 |
-0.13 |
1.28* |
0.47 |
|
MRK |
-0.41 |
1.29* |
0.25 |
-1.73* |
2.07* |
0.25 |
-1.57* |
1.98* |
0.25 |
|
PG |
-0.03 |
1.35* |
0.40 |
-0.06 |
1.39* |
0.38 |
-0.09 |
1.46* |
0.39 |
|
XOM |
-0.08 |
1.15* |
0.51 |
-0.60* |
1.59* |
0.49 |
-0.79* |
1.72* |
0.51 |
|
Среднее |
-0.01 |
1.14 |
0.50 |
-0.06 |
1.18 |
0.49 |
-0.13 |
1.24 |
0.50 |
Таким образом, модель CarrGARCH сообщает о лучших прогнозах вне выборки, в то время как наиболее часто используемый RealEGARCH сообщает о худших прогнозах.
Выводы. Модель Realized GARCH обеспечивает эффективную и гибкую основу для совместного моделирования доходности и реализованной меры. В данной работе всесторонне оценивается эффективность прогнозирования трех вариантов RealGARCH, включая наиболее часто используемые лог-линейный RealGARCH, RealEGARCH и CarrGARCH.
В ходе работы выявлено явное доминирование CarrGARCH над двумя другими конкурирующими моделями. Учитывая, что CarrGARCH имеет простейшую спецификацию модели, этот вывод согласуется с принципом экономии, что простые модели обычно имеют лучшую производительность, чем сложные. Данный вывод важен для будущего выбора модели и применения.
Литература:
- Andersen T., Bollerslev. T. Answering the Skeptics: Yes, Standard Volatility Models Do Provide Accurate Forecasts // Econometrica. 1998. Vol. 39, No 4.
- Andersen T. G., Bollerslev T., Diebold F. X., Labys P. Modeling and Forecasting Realized Volatility // Econometrica. 2003. Vol 71, No 2.
- Barndorff-Nielsen O. E., Shephard N. Econometric Analysis of Realized Volatility and Its Use in Estimating Stochastic Volatility Models // Journal of the Royal Statistical Society. 2002. Vol 64, No 2.
- Barndoff O. E., Shephard N. Power and Bipower Variation with Stochastic Volatility and Jumps // Journal of Financial Ecjnjmetrics. 2004. Vol 2, No 1.
- Barndorff-Nielsen O. E., Hansen P. R., Lunde A., Shephard N. Designing Realized Kernels to Measure the Ex-post Variation of Equity Prices in the Presence of Noise // Econometrica. 2008. Vol 76, No 6.
- Engle R. New frontiers of ARCH models // Econometrica. 2002. Vol 17.
- Shephard N., Sheppard K. Forecasting with High Frequency Based Volatility Models // Journal of Applied Econometrics. 2010.Vol 25.
- Hansen P. R., Huang Z., Shek H. H. Realized GARCH: A Joint Model for Returns and Realized Measures of Volatility //Econometrica. 2012. Vol 27, No 6.
- Hansen P. R., Huang Z. Exponential GARCH Modeling with Realized Measures // Journal of Business and Economic Statistics. 2016. Vol 34, No 2.
- Xie H. B., Qi N., Wang S. Y. A New Variant of RealGARCH for Volatility Modeling // Financial Research Letters. 2019. Vol 28.
- Dieblod F. X., Mariano R. S. Comparing Predictive Accuracy // Journal of Business & Economic Statistics. 1995. Vol 13, No 3.







