В данной работе проводится выбор автоматического линейного регулятора, обеспечивающего наименьшее изменение скорости вала двигателя при скачкообразном изменении нагрузки на валу.
Ключевые слова: система автоматической стабилизации, пропорциональный регулятор, интегральный регулятор, пропорционально-дифференциальный регулятор, закон регулирования, номинальная нагрузка.
Системы автоматического регулирования, поддерживающее постоянное (в частности, нулевое) значение регулируемой величины, называются системами стабилизации [1, с. 13].
Главной задачей таких систем является поддержание регулируемой величины на заданном уровне с допустимой ошибкой независимо от действующих возмущений. Возмущения, действующие на систему, вызывают отклонения стабилизируемой (регулируемой) величины от установленного для нее значения. Отклонение регулируемой величины — это разность, возникающая между значением регулируемой величины в определенный момент времени и её заданным значением.
Система автоматической стабилизации является совокупностью, регулируемого объекта и автоматического регулятора [1, с. 13]. Регулятор состоит из усилителя, исполнительного элемента и корректирующих элементов. Систему автоматического регулирования можно представить в виде следующей структурной схемы (рис. 1.).
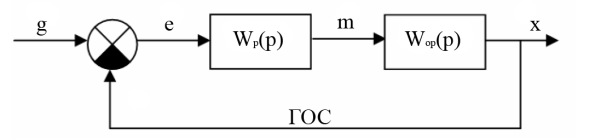
Рис. 1. Структурная схема системы автоматической стабилизации: g — входное (задающее) воздействие; e — ошибка регулирования (отклонение стабилизируемой величины); m — управляющее воздействие; Wp(p) — передаточная функция автоматического регулятора; Wор(p) — передаточная функция объекта регулирования; ГОС — главная обратная связь (отрицательная)
В системах автоматической стабилизации, состоящих из элемента сравнения, усилителя сигнала, исполнительного элемента и объекта регулирования, динамические процессы, чаще всего, не могут протекать с требуемым уровнем качества, в некоторых случаях, процесс регулирования вообще может быть неустойчивым. В связи с этим в системах автоматической стабилизации используются корректирующие устройства, в качестве одного из таких корректирующих устройств может быть использован линейный автоматический регулятор.
Несмотря на развитие микропроцессорных электронных вычислительных машин и программного обеспечения автоматические регуляторы не утратили своей актуальности и до сих пор имеют широкое применение в системах стабилизации и регулирования.
Автоматические регуляторы имеют следующие типовые законы регулирования:
- Пропорциональный закон регулирования (П — регулятор);
- Интегральный закон регулирования (И — регулятор);
- Пропорционально-интегральный закон регулирования (ПИ — регулятор);
- Пропорционально-дифференциальный закон регулирования (ПД — регулятор);
- Пропорционально-интегрально-дифференцирующий закон регулирования (ПИД — регулятор).
Пропорциональный закон регулирования
Передаточная функция П — регулятора:
![]()
где: ![]() — коэффициент передачи регулятора [2, с. 70].
— коэффициент передачи регулятора [2, с. 70].
Настройка П — регулятора осуществляется изменением только одного параметра — коэффициента передачи регулятора.
Интегральный закон регулирования
Передаточная функция И — регулятора:
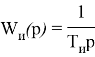
где: ![]() — постоянная времени изодрома [2, с. 70].
— постоянная времени изодрома [2, с. 70].
Настройка И — регулятора осуществляется изменением также одного параметра — постоянной времени изодрома.
Пропорционально-интегральный закон регулирования
Передаточная функция ПИ — регулятора:
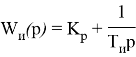
Настройка ПИ — регулятора осуществляется изменением уже двух параметров — постоянной времени изодрома и коэффициента передачи регулятора.
Пропорционально-дифференциальный закон регулирования
Передаточная функция ПД — регулятора:
![]()
где: ![]() — постоянная времени дифференцирования (постоянная времени предварения) [2, с. 71].
— постоянная времени дифференцирования (постоянная времени предварения) [2, с. 71].
Настройка ПД — регулятора осуществляется изменением уже двух параметров — постоянной времени предварения и коэффициента передачи регулятора.
Пропорционально-интегрально-дифференцирующий закон регулирования
Передаточная функция ПИД — регулятора:
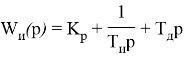
Настройка ПИД — регулятора осуществляется изменением всех трех параметров — постоянной времени предварения, коэффициента передачи регулятора и постоянной времени изодрома.
В качестве системы автоматической стабилизации будет рассмотрена система стабилизации скорости вращения вала электродвигателя постоянного тока ЭДМ-20. Структурная схема данной системы приведена на рис. 2.
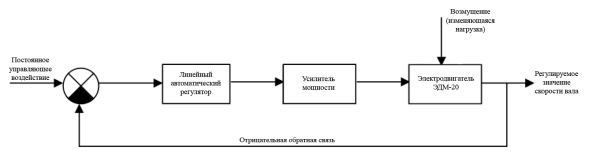
Рис. 2. Структурная схема используемой системы стабилизации скорости вращения вала электродвигателя ЭДМ-20
Используя графическую среду имитационного моделирования Simulink, проведем настройку каждого типа регулятора при номинальной нагрузке (номинальная нагрузка для электродвигателя ЭДМ-20 равна 0,57 Н•м.), настройка регуляторов будет направлена на получение минимально возможной для каждого типа регулятора величины перерегулирования [3, с. 10]. Графики изменения угловой скорости электродвигателя при номинальной нагрузке, получившиеся при использовании различных законов регулирования приведены на рис. 3.
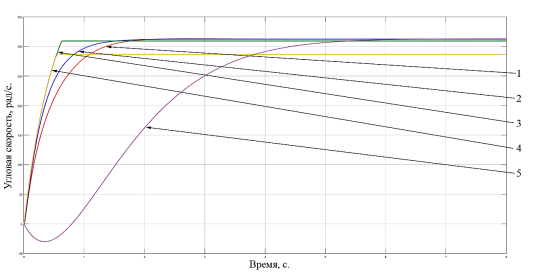
Рис. 3. Графики изменения угловой скорости электродвигателя при номинальной нагрузке, где: 1 — Пропорционально-интегрально-дифференцирующий закон регулирования; 2 — Пропорционально-интегральный закон регулирования; 3 — Пропорционально-дифференциальный закон регулирования; 4 — Пропорциональный закон регулирования; 5 — Интегральный закон регулирования
По графикам, представленным на рис. 3., определим время регулирования и ошибку стабилизации для каждого из регуляторов, полученные показатели сведем в одну таблицу (Таблица № 1).
Таблица 1
Время регулирования иошибка стабилизации системы
|
Закон регулирования |
ПИД— закон |
ПИ— закон |
ПД— закон |
П— закон |
И— закон |
|
Характеристика |
|||||
|
Время регулирования, с. |
1,27 |
0,98 |
0,57 |
0,5 |
4,21 |
|
Ошибка, рад/с. |
0 |
0 |
3,5 (1,1 %) |
25,9 (8,2 %) |
0 |
Сравним качество работы системы автоматической стабилизации при скачкообразном изменении нагрузки в пределах от номинального значения до двукратного номинального значения на валу электродвигателя, график изменения нагрузки во времени приведен на рис. 4.
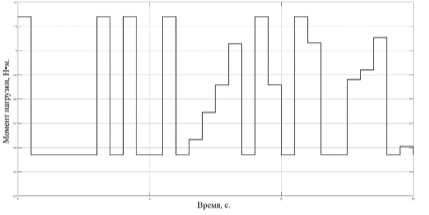
Рис. 4. График изменения нагрузки на валу двигателя во времени
Подадим сформированное скачкообразное изменении нагрузки представленное на рис. 4. на вал двигателя и снимем графики изменений угловой скорости вала двигателя во времени при изменяющейся нагрузке (рис. 5.)
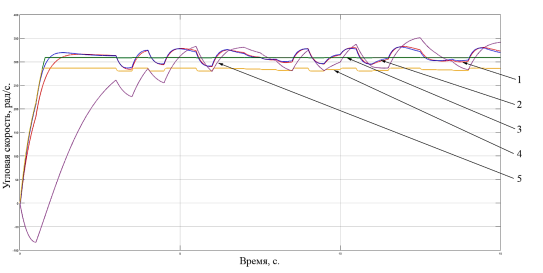
Рис. 5. Графики изменения угловой скорости электродвигателя при изменяющейся нагрузке, где: 1 — Пропорционально-интегрально-дифференцирующий закон регулирования; 2 — Пропорционально-интегральный закон регулирования; 3 — Пропорционально-дифференциальный закон регулирования; 4 — Пропорциональный закон регулирования; 5 — Интегральный закон регулирования
При сравнении линейных законов регулирования, использующихся в системах автоматической стабилизации, было установлено что пропорционально — дифференциальный закон регулирования (ПД — регулятор) обеспечивает наименьшее изменение скорости вала двигателя при скачкообразном изменении нагрузки на валу. Данный закон регулирования не позволяет добиться безошибочной стабилизации, но ошибка, получаемая при его использовании, сравнительно мала (1–2 %).
В ходе проведения аналогичного сравнения автоматических регуляторов при скачкообразном изменении нагрузки в диапазоне от ее номинального значения для данного двигателя до четырехкратного значения этой нагрузки было также определено, что пропорционально — дифференциальный закон регулирования (ПД — регулятор) обеспечивает наименьшее изменение скорости вала двигателя при скачкообразном изменении нагрузки на валу.
Подводя итог проведенной работе стоит сказать, что пропорционально — дифференциальный закон регулирования является наиболее подходящим для систем автоматической стабилизации, регулирующих скорость вращения вала электродвигателя при изменяющейся во времени нагрузке.
Литература:
- Бесекерский В. А., Попов Е. П. Теория систем автоматического регулирования. — третье издание. — М.: Наука, 1975. — 767 с.
- Копелович А. П. Инженерные методы расчета при выборе автоматических регуляторов. — М.: Государственное научно-техническое издательство литературы по черной и цветной металлургии, 1960. — 189 с.
- Баунин В. Г. Моделирование систем управления. Методические указания к лабораторным работам. — Ковров: КГТА, 2007. — 64 с.







