В статье рассмотрена иерархическая модель источника ошибок и стираний, описываемая моделью Пуртова с Марковской цепью переходов состояний при передаче данных по нестационарным каналам. Установлена зависимость степени группирования, средней кратности ошибок и ее дисперсии от длины кодового слова. Предложенная модель источника ошибок и стираний использована для оценки обнаруживаемой способности кодов и выбора оптимальной длины блока в системах передачи данных. Анализ полученных результатов исследования показывает, что выигрыш в эффективной скорости передачи при оптимальной длине блока в зависимости от текущего состояния канала составляет от 15 % до 30 %.
Ключевые слова: нестационарный канал, канал передачи данных, источник ошибок, стирания в каналах связи, канал связи, дискретный канал связи, поток ошибок, помехи, детектор качества, длина блока линейных кодов, защита от ошибок.
Многочисленные исследования показывают, что вероятностные характеристики действующих в каналах связи помех существенно изменяются во времени и являются нестационарными. В периоды увеличения интенсивности помех эффективная скорость в системах передачи данных(СПД) с решающей обратной связью (РОС) и длинными блоками резко падает, что делает практически невозможным функционирование последних. В этой связи повышение эффективной скорости передачи в системах передачи данных, без снижения верности, связано с использованием методов адаптации длины блока к изменяющимся состояниям дискретного канала. Методы адаптации длины блока целесообразно применять в дискретных каналах с несколькими состояниями, для которых известны вероятностные модели и возможно непосредственное измерение численных значений их параметров.
Одним из основных требований, предъявляемых к модели источника ошибок и стираний при передаче данных по нестационарным каналам, является полнота и гибкость модели, позволяющие оценить вероятностно–временные характеристики систем передачи данных с требуемой адекватностью и скоростью при варьировании структуры, алгоритмов и параметров системы [1,3].
При построении систем передачи данных, обеспечивающих заданную верность передачи, необходимо знать характеристики используемых каналов передачи данных. Целесообразность выбираемого метода и устройства защиты от ошибок определяется характером распределения ошибок и стираний, возникающих в дискретных каналах. Поэтому большое значение уделяют изучению и математическому описанию закономерностей возникновения ошибок и стираний в дискретных каналах связи [2,5,6].
При исследовании нестационарных каналов связи необходимо построить составную модель канала, представляющуюся в виде совокупности моделей канала, структурно взаимосвязанных и допускающих единое аналогическое представление, которая может быть использована для оценки вероятностно–временных характеристик различных алгоритмов мягкого декодировании при приеме информации по нестационарным каналам с группированием ошибок [4,5,6].
В каналах с группирующимися помехами с целью извлечения максимальной информации о них необходимо разработать составную модель нестационарных каналов передачи данных, которая может быть использована при моделировании и сравнительном анализе адаптивных систем передачи данных.
Модель источника ошибок истиранийЛ.П.Пуртова
В [3] предлагается двухпараметрическая модель источник ошибок, в соответствии с которой вероятность появления элементной комбинации с одной и более ошибками равна
Р (≥1, n) ≈n1-αp при np<<1 (1),
где — α показатель группирования ошибок (0<α<1); Р=Р(≥1, n = 1) — вероятность появления ошибочного элемента.
Вероятность появления в n — элементной комбинации ошибок кратности m и более равна [3]
![]() ∙р. (2)
∙р. (2)
Ввиду нестационарности потока ошибок во времени и случайности длины пакетов ошибок численное значение α, определяемое по экспериментальным данным с изменением n, не остается постоянным.
При группировании помех на выходе детектора качества сигналов наблюдается группирование сигналов стираний, которые также могут быть представлены моделью Л. П. Пуртова [6].
Зависимость αош(n), полученная по результатам имитационного моделирования приведена на рис.1, где с ростом n с 7 до 127 бит αош (кривая 3) возрастает с 0,52 до 0,64, а величина αст возрастает с 0,52 до 0,64. Были также оценены сигналы стираний детекторов качества (ДКС) при заданных порогах (рис. 1): при алгоритме трехточечного стробирования элементов — ДКС1, при контроле амплитуды огибающей в средней точке элементов — ДКС2, при составном — ДКС3. Зависимости αст(n) повторяют кривые αош(n) с той лишь разницей, что при менее эффективных ДКС кривая αст (n) проходит графически ниже αош(n), а при более эффективных ДКС и в случаях, когда αлс> αпс (показатели группирования ложных и правильных стираний) αст(n) размещается намного выше кривой αош(n). Коэффициенты αош и αст для всех ДКС с ростом величины n стремятся к постоянному значению.
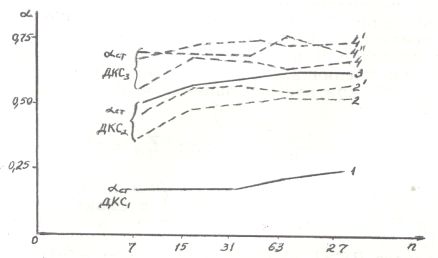
Рис. 1. Зависимость показателя группирования от длины кодового слова
Исследование зависимости средней кратности ошибок tош и пределов ее изменений от tош — σ до tош + σ от длины блока n (рис.2.) показало следующее:
– эти кривые проходят ниже кривой tош = 0.5n (случай пакетов с плотностью ошибок РЕ=0.5) и наблюдается зависимость logtош = αlogn (свидетельствует о том, что в рассматриваемом канале в пределах группирований ошибок плотность ошибок РЕ<0.5);
– кривые зависимости средней кратности стираний tст от длины блока α располагаются ниже кривой tшо =f(n).
Кривые кратности обнаруживаемых tобн.ош(n) и исправляемых ошибок tисп.ош(n) располагаются значительно ниже кривой tош(n) и тем более ниже кривой tош(n)+ σ(n) (рис.2). При группировании ошибок в реальных каналах с ростом длины блока линейных кодов tош (и тем более tош + σ) возрастает быстрее tобн(n) и tисп.(n), что свидетельствует о необходимости поиска таких кодов, в которых скорости роста tобн (n) и tисп.(n) должны превышать скорости роста tош + σ.
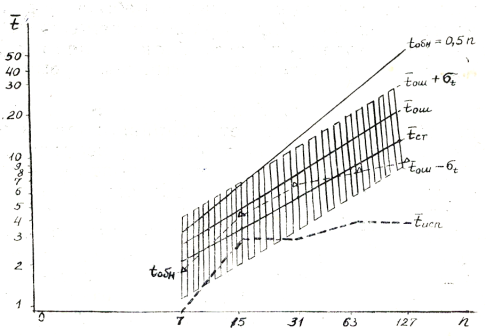
Рис. 2. Зависимость средней кратности ошибок от длины кодового слова
Составная модель источника ошибок истираний нестационарного канала связи
Так как реальные каналы связи нестационарные, а на практике в ряде ситуаций имеется возможность выделения квазистационарных участков, то для этих каналов можно использовать квазистационарную математическую модель, описываемую моделью Пуртова с Марковской цепью переходов состояний. Особенностью обобщенной модели Пуртова с Марковской цепью перехода состояний является то, что она содержит минимальное число параметров, что упрощает инженерные расчеты и описывается на базе известной модели для канала без стираний. Кроме того, с показателем группирования ![]() связан коэффициент
связан коэффициент ![]() ,численно равный среднему числу ошибочных элементов в ошибочном блоке:
,численно равный среднему числу ошибочных элементов в ошибочном блоке:
![]() (3)
(3)
Аналогичная связь существует и между показателем группирования стираний ![]() и
и ![]() .
.
Выбор параметров метода защиты от ошибок по усредненным обобщенным параметрам (![]() и
и ![]() ) гарантирует лишь статистическую оптимальность, в то время как верность и скорость передачи на конкретных локальных отрезках времени могут колебаться вокруг средних значений в весьма широких пределах.
) гарантирует лишь статистическую оптимальность, в то время как верность и скорость передачи на конкретных локальных отрезках времени могут колебаться вокруг средних значений в весьма широких пределах.
Переходные матрицы Марковской цепи имеют вид:
Для вероятности ошибок ![]() :
:
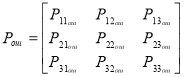
Для показателя группирования ошибок
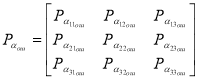
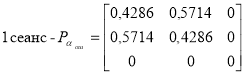



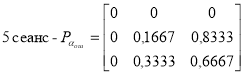
Граничные значения, разделяющие текущее состояние дискретного канала на три состояния, следующие:
1) ![]() <0,3;
<0,3;
2) 0,3<а<0,5;
3) ![]() >0,5.
>0,5.
Приведем графы переходов для
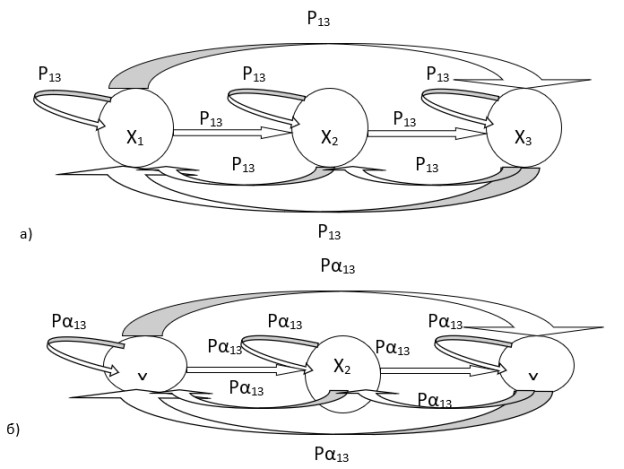
Рис. 3. Графы переходов состояния канала для: а) ![]() , б)
, б)![]()
где ![]() — вероятность ошибки;
— вероятность ошибки; ![]() — показатель группирования.
— показатель группирования.
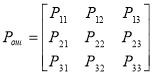
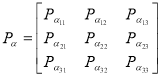
Финальные матрицы получаются путем возведения переходных матриц в степень до тех пор, пока матрица полностью не возродится в матрицу строки. Рассмотренная модель источника группирующихся ошибок и стираний позволяет оценить характеристики кодов с обнаружением и исправлением ошибок и стираний в декодерах с мягким решением при группировании ошибок и стираний в каналах связи.
Кроме того, модель источника ошибок и стираний может быть использована для оценки корректирующих способностей различных кодов и их выбора в системах передачи данных с комбинированным методом обнаружения и исправления ошибок. Для нестационарных каналов связи предлагается использовать составную модель источника ошибок и стираний, описываемую моделью Пуртова с Марковский цепью переходов.
Учитывая, что пакеты стираний включают в себя, как подмножество пакеты ошибок, то они являются предвестниками возникновения группирования ошибок и их окончания, независимо от структуры передаваемой информации. При этом эффективность контроля канальных ошибок в значительной степени зависит от характеристик используемых методов оценки качества канала связи. К последним относится выбор контролируемых параметров, зоны стирания и длины контролируемого блока. Эффективность методов оценки качества каналов связи производится по критериям корреляции и связности потоков стираний и ошибок. Распределение этих величин в зависимости от порогов стирания и длин блоков позволяет произвести оценку как информационных возможностей, так и динамических свойств методов контроля качества каналов связи [5,6].
Критерии корреляции исвязности потоков стираний иошибок.
Корреляционный критерий между потоками стираний и потоком ошибок имеет следующий вид [2,5,6]:
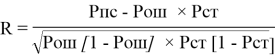
Где Рош — вероятность ошибки в канале;
Рпс — вероятность правильного стирания;
Рст — вероятность стирания.
Коэффициенты связности представлены в виде:
![]() ;
; ![]() .
.
Оценка качества канала по сигналам стираний для модели Пуртова, учитывающего группирование стираний производится с использованием выражения:
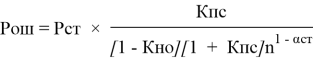
При косвенном методе таким же образом рассматривается зависимость распределения вероятности появления t — кратного стирания:
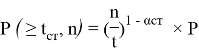
Особенность нестационарных каналов вызывает необходимость использования методов контроля качества каналов, которые обладали бы достаточно высокими обнаруживающими свойствами. В этом плане наибольший интерес предоставляют комбинированные методы обнаружения ошибок, которые находят все больше применения в современных СПД.
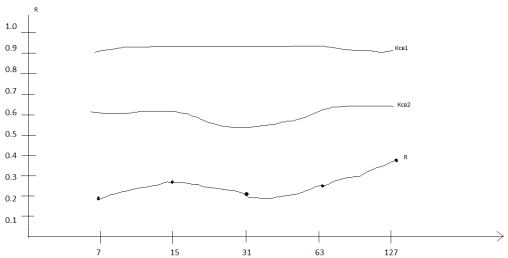
Рис. 4. Графики зависимости R, Ксв1, Ксв2 от длины кодовой комбинации n
Исследования показывают, что для составного детектора качества сигналов величина коэффициента корреляции между параметрами потока стираний и потоком ошибок достигает значения 0.8–0.9. Последнее позволяет производить оперативную оценку динамики изменения условия приёма путём задания различных состояний канала по коэффициенту стираний Кст и показателю группирований стираний αст.
Оценка эффективной скорости передачи иоптимальных длин блоков вСПД
Необходимо отметить, что в широко используемой инженерной практики модели Пуртова предполагается неизменность для заданного канала связи показателя группирования αош. Однако проведенные исследования и результаты обработки статистических данных записи потока ошибок по пяти сеансам показали, что сеансы измерения отличаются как по частости ошибок Кош, так и по величинам коэффициента группирования αош. (таблица 1). При этом значение αош существенно изменяется как от сеанса к сеансу, так и в пределах сеанса. Выбор же длины блока по критерию максимума эффективной скорости передачи, по средним значениям частости ошибок и коэффициенту группирования, гарантирует лишь статистическую оптимальность. На конкретных локальных же отрезках времени эффективная скорость может колебаться около среднего значения в весьма широких пределах.
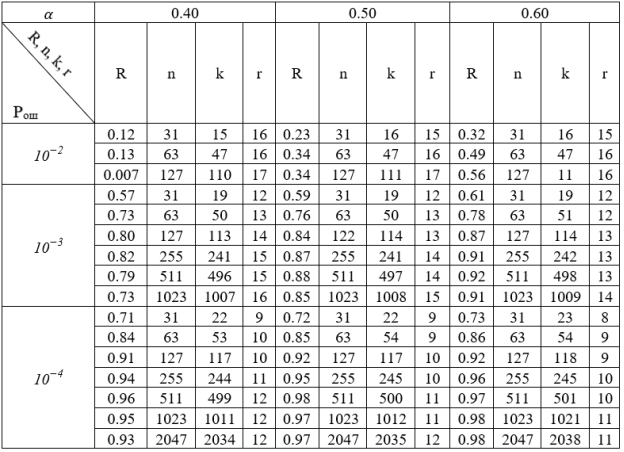
Поэтому представляет интерес оценка эффективной скорости передачи и оптимальных длин блоков и их зависимости от численных значений параметров Кош и αош. Результаты оценки эффективной скорости передачи, оптимальных значений длин блоков и параметров кода, обеспечивающих адекватность приема 1*10–6, для различных Кош и αош приведены в таблице 2. Анализ полученных результатов показывает, что выигрыш в эффективной скорости передачи, при оптимальной длине блока в зависимости от текущего состояния канала составляет от 15 % до 20 %. Так как частность стирания Кст и показатель группирования стирания αст поддается непосредственному измерению, то последние могут быть использованы в качестве контролируемых параметров при оперативном контроле за текущим состоянием канала связи и адаптивного выбора оптимальной длины блока.
Таблица 1
Значения коэффициента ошибок Кош и показатели группирования αош в различных сеансах
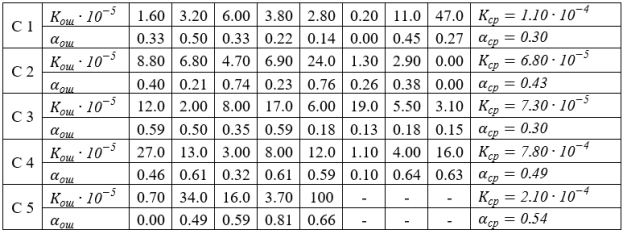
Таблица 2
Результаты расчета оптимальных длин блоков всистеме сРОС
Заключение
Одним из основных требований, предъявляемых к модели источника ошибок и стираний при передаче данных по нестационарным каналам, является полнота и гибкость модели, позволяющие оценить вероятностно–временные характеристики систем передачи данных
Для нестационарных каналов связи предлагается использовать составную модель источника ошибок и стираний, описываемую моделью Пуртова с Марковской цепью переходов.
Модель источника ошибок и стираний может быть использована для оценки обнаруживаемой способности кодов и выбора оптимальной длины блока в системах передачи данных.
Анализ полученных результатов исследования показывает, что выигрыш в эффективной скорости передачи, при оптимальной длине блока в зависимости от текущего состояния канала составляет от 15 % до 30 %.
Литература:
- Шеховцов О. И., Горохов С. Г. Передача информации по нестационарным каналам связи. Учебное пособие / Под ред. Б. Я. Советова /ЛГУ.-Л.-1985.
- Гладких А. А. Основы теории мягкого декодирования избыточных кодов в стирающем канале связи. — Ульяновск: УлГТУ, 2010.
- Элементы теории передачи дискретной информации/ Под редакцией Л. П. Пуртова. -М.: Связь, 1972.
- Иванов Ю. Д., Лозка Б. В., Козлюк Е. О.. Составная модель источника ошибок в дискретных каналах преобразования данных // Системный анализ и прикладная информатика. — 2016. — № 3. — С. 26–33.
- Шувалов В. П. Прием сигналов с оценкой их качества. -М.: Радио и связь. 1979.
- Арипов М. Н., Джураев Р. Х. Апроксимационная модель группирования стираний / Моделирование систем и процессов связи: Сб. науч. Трудов институтов связи./ Л.:ЛЭИС, 1988,с 37–43.
- Джураев Р. Х., Джаббаров Ш. Ю., Умирзаков Б. М., Хамраев Э.А Помехоустойчивые коды в телекоммуникационных системах. Учебное пособие, Ташкент, 2008.
- Иванов Ю. Д. Составная модель источника ошибок в дискретных каналах преобразования данных/Ю. Д. Иванов, Б. В. Лозка, Е. О. Козлюк // Системный анализ и прикладная информатика. — 2016. — № 3. —С.26–33.
- Вернер М. Основы кодирования. Москва: Техносфера, 2006.
- Морелос — Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. Москва: Техносфера, 2005.







