Представленный материал содержит результаты аналитического обзора литературных источников по истории математики, сбора и анализа данных, полученных в ходе изучения различных аспектов изучения математической символики, авторскую теорию формирования арабских символов путем графического изображения связей четных и нечетных чисел.
Ключевые слова: история математики, арабские символы цифр, четные и нечетные цифры, графическое изображение связей.
Возникновение арабских цифр, символы которых известны европейцам с X века, датируют примерно V веком н. э. В их основе видоизмененные в соответствии с особенностями арабского письма индийские символы. Интенсивно развивающейся после упадка Римской империи индийской школе точных наук принадлежит также наша современная десятичная позиционная система. Это наиболее известное достижение индийской математики. Первое известное нам применение десятичной позиционной системы относится к 595 г., сохранилась также плита, на которой число лет 346 записано в такой системе. Знакомство с ней арабского мира произошло благодаря торговым караванным путям и тесному общению с Индией. Самым древним упоминанием об индийской позиционной системе считается рукописный труд сирийского епископа, а также переводы с индийского аль-Фазари и научные труды Ал-Хорезми, проложившие путь математической символике и системе счисления в Европу [1].
Наиболее яркий период отработки единой десятичной системы с нулем и числовой символики, оставивший самые значительные образцы математической литературы, созданной выдающимися учеными, можно отнести к V-VII вв. [2, 3]. Вместе с тем, в отсутствии достаточного количества фактов, остается открытым вопрос о связях, взаимных влияниях математических школ Индии, арабских стран, Востока. Также недостаточно выяснен вопрос происхождения символов арабских чисел. Известный русский историк математики В. В. Бобынин писал: «История наших цифр представляет не более, как ряд предположений, перемежающихся с произвольными допущениями, производящими иногда, вследствие предшествующего употребления метода внушения, впечатления как бы чего-то доказанного. Цит. по [3:51]. Таким образом, до сих пор не существует теории, которая в полной мере объясняла происхождение арабских цифр.
Большинство теорий создания символов арабских чисел основаны на поиске связи алфавита и цифр. В данной статье представлена «Математическая теория» создания арабских цифр, которая построена на предположении, что символы чисел сформировались путем графического изображения связей четных и нечетных чисел в определенных математических квадратах «3 на 3» (рис. 1).
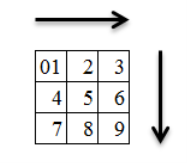
Рис. 1. Математический квадрат
На рисунке 1 представлен первый квадрат чисел. Если читать цифры в нем слева направо, то видна прямая последовательность числового ряда от одного до девяти. Предположим, что ноль относится к четному числу и находится в одной ячейке с единицей. Если подбирать связи четных и нечетных чисел таким образом, чтобы их графическое изображение в этом квадрате имело только вертикальное и горизонтальное начертание, без косых линий, то существует всего три варианта таких «связей» (рис. 2).
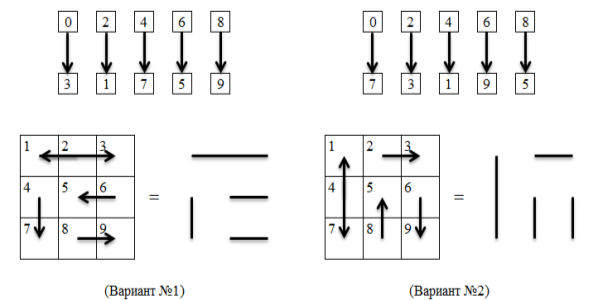
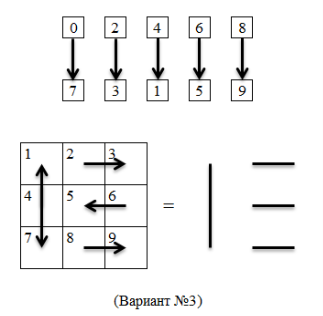
Рис. 2. Три варианта ортогонального изображения связей четных и нечетных чисел
Используем первый вариант. Соблюдая последовательность чисел от одного до девяти возможно построить всего девять квадратов. Графическое изображение первого варианта во всех девяти квадратах представлено на рисунке 3.
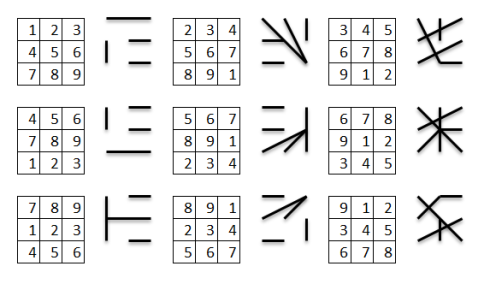
Рис. 3. Графическое изображение связей четных и нечетных чисел и производные символы
При создании символов использовались только три математических квадрата, которые начинают свой отсчет с единицы, четверки и семерки. Здесь есть правило: если в первом квадрате получается символ без косых линий, то символы в квадратах, которые начинаются с четверки и семерки, также будут ортогональны, во всех остальных случаях символы будут с косыми линиями. Таким образом, исключается использование всех остальных квадратов.
В результате данных действий получены три символа, которые составят первую группу. Вторая группа будет состоять из таких же символов, только перевернутых на 180 градусов (рис. 4).

Рис. 4. Графическое изображение полученных групп символов
Далее необходимо совместить поочередно символы первой и второй группы, как показано на рисунке 5.

Рис. 5. результаты совмещения исходных символов
В результате совмещения выведенных ранее символов получаются все арабские числа, за исключением четверки и семерки. Особое внимание заслуживает число «три», которое, в отличие от других, появляется при совмещении всех трех символов одной группы.
Символы чисел «один» и «ноль» находятся рядом. При графическом нанесении связей четных и нечетных чисел «ноль» также проецируется в одной ячейке с единицей. Арабские числа — это десятичная система, а из полученных символов видно, что «ноль» и «единица» располагаются рядом друг с другом, создавая число «десять». Этот факт особенно интересен, учитывая, что появление числа «ноль» в математике исторически совпадает с появлением арабских цифр.
Второй и третий варианты соотношения четных и нечетных чисел не дают таких результатов, поэтому не рассматриваются как исходные.
Особенность символов, которые легли в основу арабских чисел, заключается в том, что каждая линия расположена строго горизонтально или вертикально. Благодаря этому, все линии в полученных арабских числах так же не имеют косых начертаний.
Таким образом, подытоживая изложенную теорию, основанную на предположении о формировании арабских символов путем графического изображения связей четных и нечетных чисел, можно сделать вывод о том, что три символа легли в основу написания арабских цифр, за исключением четверки и семерки. Полученные символы имеют привычный для нас вид и мало изменились.
Литература:
- Стройк Д. Я. Краткий очерк истории математики. — М.: Наука. — 1990. — 256 с.
- Рыбников К. А. История математики. — М.: МГУ, 1974. — 456 с.
- Энциклопедия элементарной математики. Кн. 1. Арифметика / Под ред. П. С. Александрова, А. И. Маркушевича, А. Я. Хинчина. М.: Гос. изд-во технико-теоретической литературы, 1951. — 448 с.







