Проведенный анализ международных, зарубежных и отечественных предписаний, регламентирующих условия обеспечения безопасной транспортабельности инвалидов показал, что наиболее важным аргументом, ограничивающим возможности перемещения инвалидов, являются трудности безопасного использования инвалидами-колясочниками в качестве транспортного средства автобусов. Одновременно анализ показал, что современные конструкции автобусов не в полной мере обеспечивают безопасность инвалидам.
Международным нормативом, регламентирующим требования к обеспечению безопасной транспортабельности инвалидов, использующих инвалидные коляски, в автобусах являются предписания Правил № 107 ЕЭК ООН.
В соответствии с приложением 8 указанных Правил инвалид в коляске может размещаться в определенных конструкцией автобуса местах как в положении лицом, так и спиной по направлению движения. При размещении лицом по направлению движения инвалид должен закрепляться ремнем безопасности к коляске, а сама инвалидная коляска должна ремнями безопасности крепиться к автобусу.
Учитывая, что в городских автобусах не используются вообще ремни безопасности, то вероятность использования их для инвалидов минимальна.
Авторами была выдвинута идея размещать коляску с инвалидом в автобусе только спиной по направлению движения.
Для возможности определения возможных причин травмирования инвалидов в инвалидных колясках в автобусах, было признано необходимым провести математическое моделирование динамики инвалида в коляске в условиях характерного типа ДТП, каким является фронтальное столкновение.
В исследовании была поставлена задача определить характеристики движения инвалида, которые могли бы быть причиной его травмирования. Были приняты начальные условия, когда коляска полностью заторможена и неподвижна относительно автобуса. Пассажир сидит спиной к направлению движения.
Динамическая модель системы приведена на рис. 1 и 2.
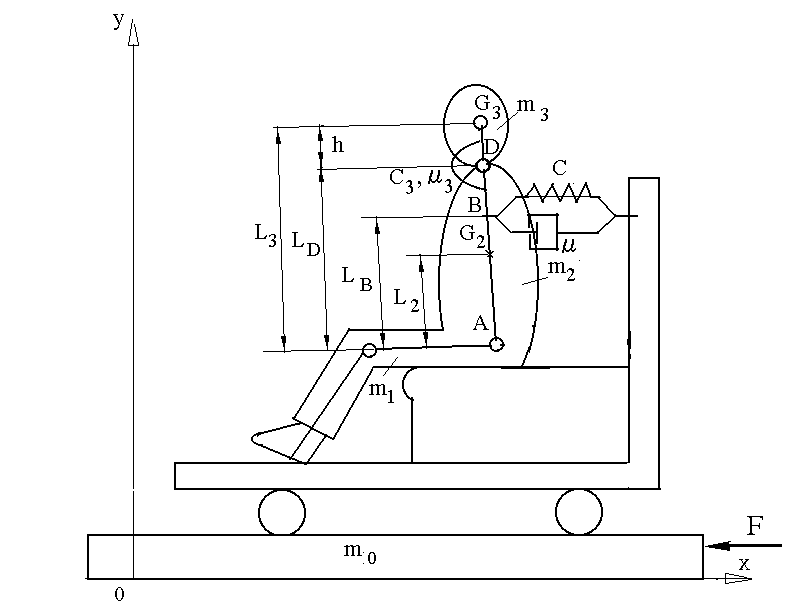
Звено m1 может двигаться поступательно вместе с условным шарниром А. Звено m2 может поворачиваться вокруг шарнира А, а звено m3 – поворачиваться вокруг условного шарнира D. Автобус движется в сторону оси ОХ.
Рисунок 1. Динамическая модель системы«автобус-инвалидная коляска-инвалид»
G2, G3 – центры тяжести звеньев m2, m3,
L2, LB, LD, L3 – расстояния от условного шарнира А до соответствующих точек,
h – расстояние от условного шарнира D до центра тяжести головы.
С, μ – приведенные жесткость и коэффициент демпфирования спинки кресла,
С3, μ3 – угловые жесткость шеи и коэффициент ее демпфирования,
[С3] = (Н·м)/рад, [μ3] = (Н·м·с)/рад.
Модель имеет четыре степени свободы, и ее движение определяется следующими обобщенными координатами:
х – абсолютная координата положения инвалидной коляски,
x1 – относительная координата звена m1 (относительно автобуса),
φ2 – угловая координата звена m2 (угол поворота туловища),
φ3 – угловая координата звена m3 (угол поворота головы).
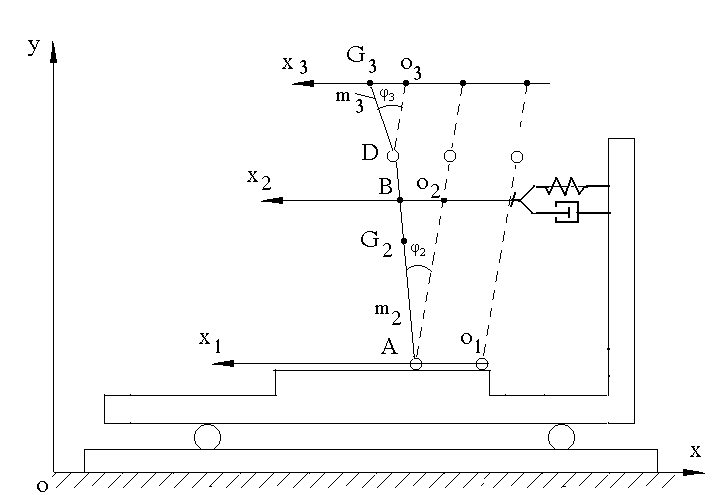
Координаты отсчитываем от начальных положений звеньев (см. рисунок. 2).
Рисунок 2. Характер изменения положений звеньев системыпри воздействии силы F.
Автобус с пассажиром, движущийся со скоростью V0, затормаживается силой F, обеспечивающей трапециадальное изменение замедления.
Для составления уравнений движения применяем уравнения Лагранжа второго рода.
|
(1) |
где: Т – кинетическая энергия системы, выраженная через обобщенные координаты и обобщенные скорости,
Qx, Q1, Q2, Q3 – обобщенные силы, соответствующие выбранным обобщенным координатам.
Вычисление кинетической энергии проводим с использованием схемы, изображенной на рисунок 2.
где:
m0 – масса автобуса с инвалидной коляской,
V2 – скорость центра тяжести звена 2 (точка G2 на рис. 2),
V3 – скорость центра тяжести головы и шеи (точка G3 на рис. 2),
J2, J3 – моменты инерции туловища и головы относительно горизонтальных осей, проходящих через их центры тяжести.
Выражаем V2 и V3 через обобщенные координаты системы:
где x2, y2, x3, y3 – абсолютные координаты точек G2, G3.
Из рис. 2 находим:
x2 = x - x1 - L2sinφ2,
y2 = L2 cosφ2 + H,
H =const – высота сидения.
Аналогично:
x3 = x - x1 - LDsinφ2 - hsinφ3,
y3 = LDcos φ2 + h cos φ3 + H,
Подставляя полученные значения в уравнение (2), ограничиваясь первыми членами разложения sin φ2, cos φ2 , sin φ3, cos φ3 в ряды Тейлора и не учитывая слагаемые выше второго порядка, получаем:
Использование этого выражения в уравнениях (1) приведет к очень сложным дифференциальным уравнениям движения системы. Для решения поставленных задач необходим упрощенный вариант уравнений.
Заметим, что принятие приближенного выражения кинетической энергии (3), приводит к тому, что все частные производные кинетической энергии по обобщенным координатам равны нулю.
Подставляя выражения частных производных и обобщенных сил в уравнения Лагранжа и выполняя преобразования, получаем:
|
при 0 <t<t1
при t1 ≤ t ≤ t2
при t2 ≤ t ≤ t3
|
Система дифференциальных уравнений совместно с приведенными выше условными выражениями была проинтегрирована численным методом с использованием матричных преобразований.
После интегрирования дифференциальных уравнений получили кинематические уравнения движения пассажира в виде:
x1=
x1 (t),
x2 = x2
(t), x3
= x3 (t),
а угловая скорость головы![]() .
.
Для моделирования на ЭВМ был составлен комплект программ.
Числовые значения параметров заданы следующими:
m1 = 27 кг – масса бедер и голени пассажира,
m2 = 43.5 кг – масса туловища и рук,
m3 = 4.5 кг – масса головы пассажира,
J2 – момент инерции туловища и рук относительно оси, проходящей через их центр тяжести (точка G2 на рис. 2),
J3 – момент инерции головы пассажира относительно ее центра тяжести (точка G3).
При моделировании было приближенно принято:
С3 = 100 Н·м/рад,
μ3= 10 Н·м·с/рад.
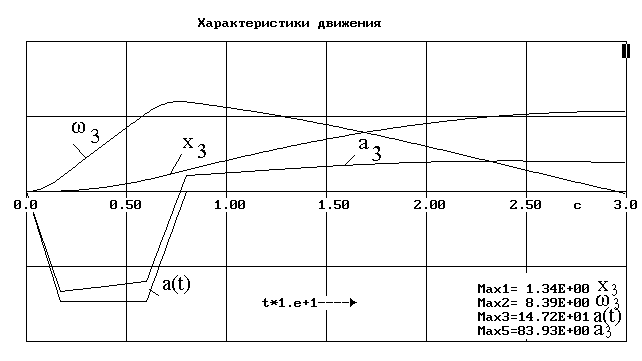
На рис. 3 приведены графики характеристик движения пассажира в функции времени, получаемые при моделировании на ЭВМ. Замедление автобуса при столкновении задано равным 150 м/с2. При таком замедлении угловая скорость головы оказалась значительной и составила 8,39 рад. с-1 .
Рисунок 3 Изменение параметров системы при столкновении автобуса.
X3 - координата центра тяжести головы относительно кресла,
&#;3 - угловая скорость головы,
а(t)– заданное замедление автобуса при наезде на препятствие,
а3 – ускорение головы.
(Максимальные числовые значения переменных, выведенных на графиках, определялись автоматически, и распечатаны в нижнем правом углу рисунков.)
Числовые значения параметров системы в программах можно легко изменять, поэтому моделирование на ЭВМ позволяет достаточно просто определять все необходимые характеристики движения автобуса с пассажиром в инвалидной коляске. Экспериментальные исследования подтвердили объективность полученных выводов.
Тяжесть травмирования человека в автомобиле при ДТП типа «удар сзади» определяется в основном повреждениями шейных позвонков. Многочисленные исследования и тесты позволили получить зависимости значений повреждаемости шейного участка позвоночника человека при «хлыстообразном» нагружении, определяемые угловым ускорением головы и длительностью действия нагрузок. Согласно этим исследованиям даже относительно небольшое угловое ускорение головы пассажира в совокупности с довольно продолжительным временем воздействия может вызвать серьезное повреждение шейного участка позвоночника. В связи с этим необходимо свести к минимуму вероятность начала углового вращения головы пользователя инвалидной коляски, например, за счет изменения конструкции опорной панели (зазор между головой инвалида и опорной панелью должен быть минимален).
Таким образом, проведенное математическое моделирование позволило сделать вывод, что при размещении инвалида в коляске спиной по направлению движения автобуса можно обеспечить его безопасную транспортабельность даже без использования ремней безопасности за счет предотвращения углового перемещения головы.