The article presents different ways of solving functional equations that occur in olimpiads and contests.
В статье представлены разные способы решения функциональных равенств, которые встречаются на олимпиадах и на конкурсах.
-
Find all functions
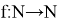 such that
such that
![]() is nonzero and
is nonzero and ![]() holds for all
holds for all ![]() [1].
[1].
Solution: Let ![]() be the assertion
be the assertion ![]() .
.
From ![]() we get
we get![]()
![]() :
: ![]() and
and
![]() , so
, so
By subtracting the second equation from the first we get
![]() (*). Now: Let
(*). Now: Let ![]() be the assertion
be the assertion
![]() We have
We have ![]() , so
, so
![]() Again by subtracting the second equation from the first we get:
Again by subtracting the second equation from the first we get: ![]() Now for
Now for ![]() ,
,
![]() We know natural divisors of
We know natural divisors of ![]() are
are ![]() Then
Then ![]() must be equal one of these
must be equal one of these ![]() . So we consider eight cases:
. So we consider eight cases:
1) Suppose ![]() .
.
In (*) from ![]() ,
, ![]() is clear and
is clear and ![]() such
such ![]() prime number is not exist.
prime number is not exist.
2) Suppose ![]() . From (*),
. From (*), ![]() .
. ![]() is clear and in
is clear and in ![]() we have
we have ![]()
![]() such
such ![]() prime number is not exist.
prime number is not exist.
3) Suppose ![]() . From (*),
. From (*), ![]()
In ![]() ,
, ![]() Contradiction.
Contradiction. ![]() is satisfied.
is satisfied. ![]() is not satisfied.
is not satisfied.
For
4) Suppose ![]() . In (*),
. In (*), ![]() For any prime
For any prime ![]() ,
,
![]() .
. ![]() such
such ![]() prime number is not exist.
prime number is not exist.
5) ![]() . Such as can not be.
. Such as can not be.
6)Suppose ![]() . In (*),
. In (*), ![]()
![]() But for any prime
But for any prime ![]() ,
,
![]() .
. ![]() such
such ![]() prime number is not exist
prime number is not exist
7) ![]() . Such as can not be.
. Such as can not be.
So for any ![]() ,
, ![]() Now from
Now from ![]()
![]() . From this we get
. From this we get
![]()
![]()
![]() By subtracting the second equation from the first we get:
By subtracting the second equation from the first we get: ![]() And also we have
And also we have
![]()
![]() Now assume
Now assume ![]() . Then
. Then ![]() and for
and for ![]() prime numbers,
prime numbers, ![]()
![]() From this
From this ![]() But for enough large
But for enough large ![]() - prime number this is not true, because,
- prime number this is not true, because, ![]() such
such ![]() - prime number infinite. Contradiction. So we conclude,
- prime number infinite. Contradiction. So we conclude, ![]() such
such ![]() is not exist.
is not exist. ![]() For
For ![]() ,
,
![]()
-
Find all functions
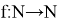 such that
such that 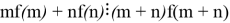 holds for all
holds for all 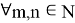 [2].
[2].
Solution: ![]() be the assertion
be the assertion ![]() .
.
![]() :
: ![]() Now consider this set
Now consider this set ![]() . Values of elements of
. Values of elements of ![]() are bounded, lies between
are bounded, lies between ![]() and
and ![]() . Let
. Let ![]() the smallest. We have
the smallest. We have ![]() .
. ![]() . But because of
. But because of ![]() the smallest,
the smallest, ![]() so for
so for ![]() . Now assume
. Now assume ![]() .
. ![]() :
: ![]() Also we have
Also we have ![]() In this for
In this for ![]() (
(![]()
Then ![]() .
. ![]() this number is positive and costanta, but
this number is positive and costanta, but ![]() is unbounded. Contradiction. So we get
is unbounded. Contradiction. So we get ![]() . From this equality we conclude the biggest element’s value and the smallest element’s value of
. From this equality we conclude the biggest element’s value and the smallest element’s value of ![]() are equal.
are equal. ![]() All element’s value of
All element’s value of ![]() equal to
equal to ![]() .
. ![]()
![]() .
. ![]() :
: ![]() and
and ![]()
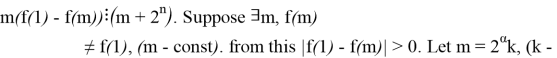 toq
toq![]()
![]() For
For ![]() ,
, ![]() from this,
from this, ![]()
![]()
So, ![]() But
But ![]() unbounded, but
unbounded, but ![]() is positive
is positive ![]() Contradiction. So, such
Contradiction. So, such ![]() is not exist.
is not exist. ![]() ,
, ![]() This is indeed a solution.
This is indeed a solution.
-
Find all functions
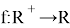 such that for all
such that for all 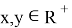
![]() [3].
[3].
Solution:
![]() : (here
: (here ![]() )
) ![]() .
.
![]() :
: ![]()
From this ![]() Now for
Now for ![]() ,
, ![]() (**).
(**).
![]() :
: ![]() .
.
![]() :
: ![]()
![]() .
. ![]() :
: ![]() :
: ![]() From (**).
From (**).
![]() :
: ![]() For
For ![]() . (
. (![]() is clear).
is clear). ![]() for all
for all ![]() . This is indeed a solution
. This is indeed a solution
-
Find all functions
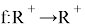 for all
for all 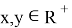
![]() [3].
[3].
Solution: ![]() be the assertion
be the assertion ![]() .
.
![]() :
: ![]() injective and
injective and ![]()
![]() :
: ![]() . In this equality
. In this equality ![]() :
: ![]() .
.
![]() :
: ![]()
![]() Because of
Because of ![]() injective:
injective: ![]()
![]() or
or ![]() If
If ![]() , from
, from ![]() Contradiction
Contradiction ![]() We have the following equalities:
We have the following equalities:
![]() :
: ![]()
![]()
![]() :
: ![]() (in (**)
(in (**) ![]() :
:
![]() ). Because of
). Because of ![]() injective:
injective:
![]() . In this equality
. In this equality ![]() :
: ![]() . From (***):
. From (***): ![]() .
. ![]() we can write (***):
we can write (***): ![]()
![]() :
: ![]() (****)
(****) ![]() :
: ![]() .
. ![]()
![]()
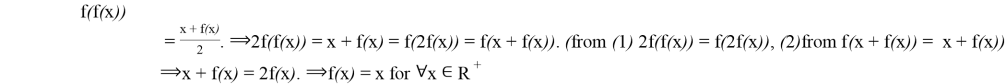 .
.
-
Find all functions
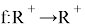 for all
for all 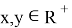 [1].
[1].
![]() .
.
Solution: ![]() be the assertion
be the assertion ![]() (*).
(*).
![]() :
: ![]()
![]() :
: 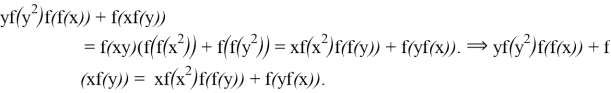 In this equality
In this equality ![]()
![]() . using this equality we can rewrite (*).
. using this equality we can rewrite (*).
![]() :
: ![]() :
: ![]() 2
2![]() . In this equality
. In this equality ![]() :
:
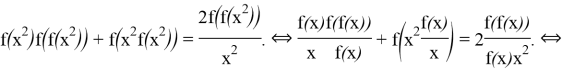
![]() Now using this and (**) we get
Now using this and (**) we get
![]() . So
. So ![]() .
. 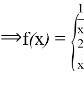 (****). Assume
(****). Assume ![]() :
: ![]() (
(![]() :
: ![]()
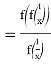 ).
). ![]() from (***)
from (***)
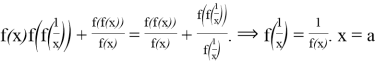 :
: ![]() But from (****)
But from (****) ![]() or
or ![]() Contradiction.
Contradiction. ![]() Such
Such ![]() is not exist.
is not exist. ![]() ,
, ![]()
-
Find all functions
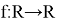 such that for
such that for 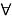
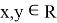 the following equalities hold:
the following equalities hold:
![]()
![]() ,
, ![]() .
.
Yechim: ![]() be the assertion
be the assertion ![]() .
.
![]() :
: ![]()
![]() :
: ![]() (*).
(*).
Let
![]() :
: ![]() :
: ![]() Contradiction.
Contradiction.
![]() -case: suppose
-case: suppose ![]() . In (*)
. In (*) ![]() :
: ![]() So,
So, ![]() If
If ![]() then from
then from ![]() we get
we get ![]() . So
. So ![]() If
If ![]() , according to second condition,
, according to second condition, ![]() .
.
![]() -case:
-case: ![]() .
. ![]() :
: ![]()
![]() .
. ![]() :
:
![]() :
: ![]() Using this and (**), for
Using this and (**), for ![]()
![]() ,
, ![]() (***).Using this we can rewrite initial equality:
(***).Using this we can rewrite initial equality:
![]() from (***)
from (***) ![]() For
For
![]() :
: ![]()
![]() So,
So, ![]()
In (****) ![]() :
: ![]()
![]() ,
, ![]() From (***), for
From (***), for ![]()
![]() ,
, ![]()
References:
- www.artofproblemsolving.com/community/c482986. IMO Shortlisted problems 2016.
- Mohammad Mahdi Taheri. “Functional equations in mathematical competitions: Problems and solutions” July 1, 2015.
- Ozgur Kircak. “Functional equations” April 8, 2011.







