Важнейшим параметром системы автоматического управления (САУ) является ее поведение при внешнем воздействии, данный параметр определяется устойчивостью.
Устойчивость САУ — это свойство системы возвращаться в исходный или близкий к нему установившийся режим после каждого выхода из него в результате какого-либо воздействия [1].
Целью данной работы является выявление зависимости между коэффициентами характеристического уравнения второго порядка, описывающего импульсную САУ, и устойчивостью системы.
Импульсные САУ — это системы автоматического управления, в которых действуют сигналы, квантованные по времени [1].
Пусть дано уравнение второго порядка, описывающее импульсное САУ:
![]()
Где a,b,c, k — коэффициенты, x- входная величина, y-выходная величина.
Для того чтобы определить устойчивость системы по одному из критериев, критерию Гурвица необходимо найти передаточную функцию системы.
Передаточная функция определяется как отношение изображений Лапласа выходной и входной величин при нулевых начальных условиях [1].
К уравнению (1) применим преобразование Лапласа:
Передаточная функция W(z):
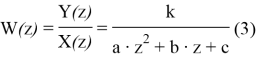
Для того чтобы использовать критерий Гурвица для импульсных САУ в выражении (3) введем замену переменной:

Тогда:

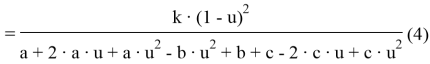
Окончательно преобразовав выражение (4), получим:
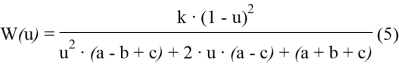
Для уравнения второй степени, по критерию Гурвица, положительность коэффициентов при u в знаменателе передаточной функции оказывается необходимым и достаточным критерием устойчивости [1].
Исходя из вышесказанного и выражения (5) можно сделать вывод, что для устойчивости импульсной САУ второго порядка необходимо выполнение всех трех неравенств:
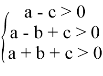
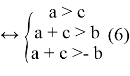
Для проверки верности данного вывода используем другой критерий устойчивости, корневой критерий.
Корневой метод определения устойчивости импульсной САУ: для того, чтобы импульсная система считалась устойчивой необходимо, чтобы корни характеристического уравнения принадлежали окружности на комплексной плоскости радиусом 1 и центром в начале координат [1].
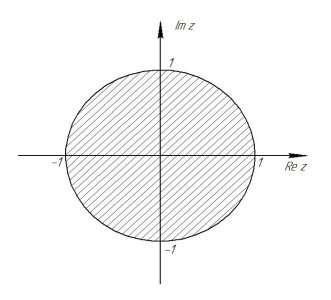
Рис. 1. Корневой метод определения устойчивости импульсной САУ
В ходе выполнения проверки было установлено, что критерий (6) является не полным, так как, например, при коэффициентах a=-5, b=3, c=1, неравенства (6) не выполняются, однако по корневому условию САУ является устойчивой.

Рис 2. Положение корней характеристического уравнения при a=-5, b=3, c=1 на комплексной плоскости
Поэтому, условие (6) нуждается в дополнении.
При определении устойчивости импульсной разомкнутой САУ второго порядка корневым методом, корнями уравнения ![]() будут значения:
будут значения: ![]() и
и ![]() , где x — действительная часть комплексного числа, iy — мнимая часть комплексного числа,
, где x — действительная часть комплексного числа, iy — мнимая часть комплексного числа, ![]() — мнимая единица.
— мнимая единица.
По теореме Виета:
![]() (7)
(7)
То есть:
![]() (8)
(8)
![]() (9)
(9)
Известно, что уравнение окружности с центром в начале координат:
![]()
![]()
Следовательно:
![]() (11)
(11)
Чтобы дискретная САУ была неустойчивой, нужно чтобы корни характеристического уравнения не выходили за пределы окружности R=1, то есть:
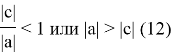
Объединяя найденные условия устойчивости (6) и (12), получим:
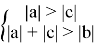 (13)
(13)
Вывод: в данной работе было выявлена зависимость (13) между коэффициентами характеристического уравнения второго порядка, описывающего импульсную САУ, и устойчивостью системы.
Литература:
- Юревич Е. И. Теория автоматического управления. — 4-е изд., перераб. и доп. — СПб.: БХВ-Петербург, 2016. — 560 с.







