В статье рассматриваются колебания корпуса бортовой радиоэлектронной аппаратуры в том случае, когда его центр тяжести не расположен над центром упругости опор. Проводится обоснование обобщения координат. Дается методика выяснения возможности «пробоя» упругих опор. Решение задачи приводится в главных координатах.
Ключевые слова: колебания корпуса, центр тяжести, центр упругости опор, обобщение координат.
The article deals with the oscillations of the hull of the onboard radio-electronic equipment in the case when its center of gravity is not located above the center of elasticity of the dispute. The substantiation of generalizations of coordinates is carried out. The method of finding out the possibility of «breakdown» of elastic supports is given. The solution is given in the main coordinates.
Key words: body vibrations, center of gravity, supports elasticity, generalizations of coordinates.
Введение.
Рассмотрим колебания корпуса, габариты которого по длине больше, чем по ширине. Такую задачу можно рассматривать как плоскую. На рис. 1 приведена схема упругой установки корпуса на колеблющейся платформе [1, 2].
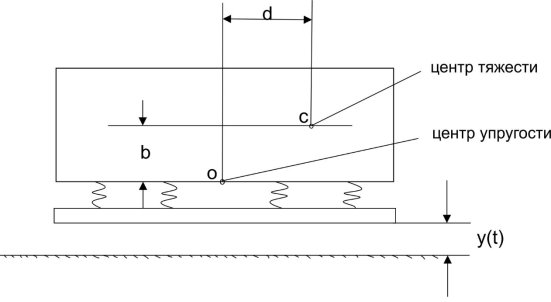
Рис. 1.
Центром упругости является точка приложения к корпусу равнодействующей статически неуравновешенных сил упругости подвески. Координаты центра упругости в произвольно выбранной системе координат определяются по выражениям:
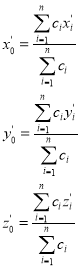 . (1)
. (1)
Здесь:
![]() ,
, ![]() ,
, ![]() — координаты центра упругости в произвольно выбранной системе координат;
— координаты центра упругости в произвольно выбранной системе координат;
![]() ,
, ![]() ,
, ![]() — координаты крепления к корпусу i-й упругой опоры в произвольно выбранной системе координат;
— координаты крепления к корпусу i-й упругой опоры в произвольно выбранной системе координат;
![]() — коэффициент упругости i-й опоры;
— коэффициент упругости i-й опоры;
n — число упругих опор.
Очевидно, что перенос начала координат в центр упругости приводит к выражениям:
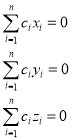 .(2)
.(2)
Здесь ![]() ,
, ![]() ,
, ![]() — координаты крепления к корпусу i-й опоры относительно центра упругости.
— координаты крепления к корпусу i-й опоры относительно центра упругости.
Для того чтобы в дальнейшем иметь возможность воспользоваться уравнениями Лагранжа второго рода, необходимо движение корпуса задать в обобщённых, т. е. независимых между собой координатах, определяющих положение корпуса в любой момент времени. Такими независимыми между собой параметрами являются вертикальное поступательное перемещение корпуса вместе с центром упругости и поворот корпуса вокруг поперечной оси, проходящей через центр упругости [3, 4].
Действительно, если приложить к корпусу только вертикальную силу, линия действия которой проходит через центр упругости, то момент статически неуравновешенных сил упругости подвески относительно центра упругости будет равен нулю:
![]()
или
![]() ,
,
но
![]() ,
, ![]() .
.
Следовательно, ![]() . (3)
. (3)
Таким образом, в случае действия вертикальной силы, приложенной к центру упругости, корпус получит только вертикальное поступательное перемещение вместе с центром упругости.
Если же приложить к корпусу в вертикальной плоскости только момент, то главный вектор статически неуравновешенных сил упругости подвески будет равен нулю:
![]()
или
![]() ,
,
но
![]() ,
, ![]() .
.
Следовательно,![]() . (4)
. (4)
Таким образом, в случае действия в вертикальной плоскости момента корпус получит только поворот вокруг поперечной оси, проходящей через центр упругости.
Следует отметить, что вертикальное поступательное перемещение корпуса вместе с центром тяжести и поворот корпуса вокруг поперечной оси, проходящей через центр тяжести, принимаемые обычно за обобщенные координаты, в случае несовпадения центра тяжести с центром упругости будут взаимозависимыми параметрами (при изменении одного из них изменяется другой) и не могут быть использованы как обобщенные координаты [5, 6].
Действительно, если приложить к корпусу только вертикальную силу, линия действия которой проходит через центр тяжести, то момент статически неуравновешенных сил упругости подвески относительно центра тяжести будет равен нулю:
![]() .
.
Здесь d — расстояние по горизонтали между центром тяжести и центром упругости.
![]()
или
![]() ,
,
но
![]() ,
, ![]() .
.
Следовательно,
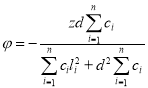 .(5)
.(5)
Таким образом, в случае действия вертикальной силы, приложенной к центру тяжести, корпус одновременно с вертикальным поступательным перемещением вместе с центром тяжести на величину z получит угловое перемещение на угол φ вокруг поперечной оси, проходящей через центр тяжести [7, 8].
Если не приложить к корпусу только поворачивающий момент в вертикальной плоскости, то главный вектор статически неуравновешенных сил упругости должен быть равен нулю:
![]()
или
![]() ,
,
но
![]() ,
, ![]() .
.
Следовательно,
![]() . (6)
. (6)
Таким образом, в случае действия в вертикальной плоскости момента корпус одновременно с угловым перемещением на угол φ вокруг поперечной оси, проходящей через центр тяжести, получит вертикальное поступательное перемещение вместе с центром тяжести на величину z.
На основании всего вышесказанного при упругой установке корпуса, когда его центр тяжести не совпадает с центром упругости, обобщенными координатами являются вертикальное поступательное перемещение корпуса вместе с центром упругости -zиповорот корпуса на угол φ вокруг поперечной оси, проходящей через центр упругости [9, 10].
При исследовании колебаний корпуса, установленного упруго на колеблющейся платформе (схема установки приведена на рис. 1), предполагаем, что масса установленной радиоэлектронной аппаратуры существенно меньше массы колеблющейся платформы, и поэтому установка аппаратуры не изменит закона колебаний платформы. Примем колебания платформы за некоторую сумму вертикальных гармонических колебаний, так как для большинства транспортных машин, на которых устанавливается бортовая радиоэлектронная аппаратура, ![]() представляет собой наложение нескольких высокочастотных колебаний на основные низкочастотные.
представляет собой наложение нескольких высокочастотных колебаний на основные низкочастотные.
![]() , (7)
, (7)
где ![]() и
и ![]() — амплитуда и частота j-го гармонического колебания.
— амплитуда и частота j-го гармонического колебания.
Кинетическая энергия колеблющегося корпуса и потенциальная энергия его упругой многоточечной опоры, записанные в обобщенных координатах, имеют вид:
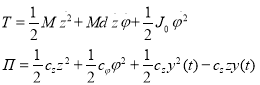 . (8)
. (8)
Здесь:
M — масса корпуса;
![]() — момент инерции корпуса относительно поперечной оси, проходящей через центр упругости;
— момент инерции корпуса относительно поперечной оси, проходящей через центр упругости;
d — абсцисса центра тяжести корпуса относительно центра упругости;
![]() — коэффициент упругости опоры при вертикальных перемещениях корпуса;
— коэффициент упругости опоры при вертикальных перемещениях корпуса;
![]() — коэффициент упругости опоры при угловых перемещениях корпуса.
— коэффициент упругости опоры при угловых перемещениях корпуса.
Кинетическая энергия колеблющегося корпуса, записанная в обобщенных координатах, содержит член с произведением обобщенных скоростей, в результате чего дифференциальные уравнения колебаний корпуса будут взаимосвязанными. Поэтому, проведя линейное однородное преобразование координат
![]() , (9)
, (9)
перейдем к так называемым главным, или нормальным, координатам ![]() и
и ![]() . Известно, что кинетическая энергия системы, записанная в главных координатах, не содержит члена с произведением главных скоростей, а потенциальная энергия не содержит члена с произведением главных координат. Используя эти положения, значения постоянных коэффициентов
. Известно, что кинетическая энергия системы, записанная в главных координатах, не содержит члена с произведением главных скоростей, а потенциальная энергия не содержит члена с произведением главных координат. Используя эти положения, значения постоянных коэффициентов ![]() и
и ![]() определяем из выражения:
определяем из выражения:
![]() . (10)
. (10)
Здесь:
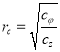 — коэффициент распределения упругих опор;
— коэффициент распределения упругих опор;
![]() — радиус инерции корпуса относительно поперечной оси, проходящей через центр упругости.
— радиус инерции корпуса относительно поперечной оси, проходящей через центр упругости.
Кинетическая энергия колеблющегося корпуса и потенциальная энергия его упругой опоры, записанные в главных координатах, имеют вид:
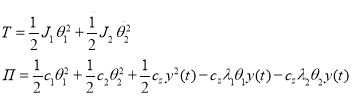 , (11)
, (11)
где
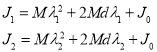 , (12)
, (12)
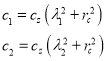 .(13)
.(13)
Используя уравнения Лагранжа второго рода
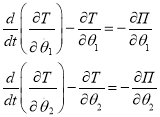 , (14)
, (14)
получим дифференциальные уравнения колебаний корпуса в главных координатах:
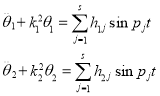 , (15)
, (15)
где
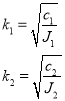 , (16)
, (16)
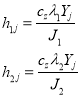 . (17)
. (17)
Решение дифференциальных уравнений (15) (при ![]() и
и ![]() ) может быть записано в виде:
) может быть записано в виде:
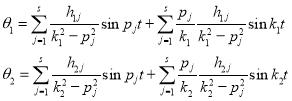 . (18)
. (18)
Угловое и вертикальное перемещение корпуса, определяемое обобщенными координатами z и φ, получим, используя преобразование (10). Деформации упругих опор корпуса будут равны:
![]() . (19)
. (19)
Здесь ![]() — абсцисса точки крепления i-й опоры к корпусу.
— абсцисса точки крепления i-й опоры к корпусу.
Если колебания корпуса находятся в пределах перемещений крайних упругих опор, допускаемых ограничителями, то его вертикальное и угловое ускорения определяются из выражения:
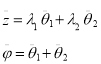 . (20)
. (20)
Выводы.
Однако, как только деформация одного из крайних упругих элементов достигнет значения, допускаемого ограничителями перемещения соответствующего элемента, будет иметь место удар в ограничитель, или так называемый «пробой» упругой опоры, определяющийся в основном низкочастотными составляющими колебаний. Ускорения удара, как известно, многократно превышают ускорения гармонических колебаний. Поэтому рассмотренное выше выяснение возможности «пробоя» упругой опоры при заданных колебаниях платформы представляет практический интерес для выяснения условий работы, надежности и долговечности бортовой радиоэлектронной аппаратуры и упругих опор ее корпуса.
Литература:
- Rosenberg L. R.,Schmidt R. V.,Coldren L. A. Interior-surface acoustic waveguiding in capillaries / Applied Physics Letters. — 1974. — vol. 25, No. 6. — P. 324–326.
- Safarov I. I., Teshayev M. H., Boltayev Z. I., Akhmedov M.Sh. Mathematical modeling of dynamic processes in a toroidal and cylindrical shell interacting with a liquid.Raleigh, North Carolina,USA: Open Sciense Publishing, 2018. 223 p.
- Safarov I. I., Teshaev M.Kh.,Akhmedov M. S. Free Oscillations of a Toroidal Viscoelastic Shell with a Flowing Liquid. American Journal of Mechanics and Applications. 2018; 6(2): 3749 http://www.sciencepublishinggroup.com/j/ajmadoi:10.11648/j.ajma.20180602.11. ISSN: 2376–6115 (Print); ISSN: 2376–6131 (Online)
- Сафаров И. И., Умаров А. О. Воздействие продольных и поперечных волн на цилиндрические слои с жидкостью// Вестник пермского университета. Математика. Механика. Информатика. 2014 Вып.3(26). с. 69–75
- Адамов А. А., Матвеенко В. П., Труфанов Н. А., Шардаков И. Н. Методы прикладной вязкоупругости. Екатеринбург: УрО РАН, 2003, 411с.
- Fedorov A.Yu., Matveenko V. P., Shardakov I. N. Numerical analysis of stresses in the vicinity of internal singular points in polymer composite materials. International Journal of Civil Engineering and Technology. Vol. 9, Iss. 8, 2018, Pp. 1062–1075.
- Bykov A. A., Matveenko V. P., Shardakov I. N., Shestakov A. P. Shock wave method for monitoring crack repair processes in reinforced concrete structures. Mechanics of Solids. Vol. 52, Iss. 4, 2017, Pp. 378–383.
- Mirsaidov M. M., Sultanov T. Z. Use of linear heredity theory of viscoelasticity for dynamic analysis of earthen structures. Soil Mechanics and Foundation Engineering, 2013. Vol. 49, Iss. 6, Рp. 250–256.
- Mirsaidov M. M., Sultanov T. Z., Rumi D. F. An assessment of dynamic behavior of the system «structure — Foundation» with account of wave removal of energy. Magazine of Civil Engineering. 39(4), Pp. 94–105.
- Koltunov M. A., Mirsaidov M.M.,Troyanovskii I. E.Transient vibrations of axissymmetric viscoelastic shells. Polymer Mechanics Vol.14, Iss.2, Pp. 233–238.







