Введение
Математическое моделирование становится актуальным в случаях, когда существуют ограничения возможностей экспериментального исследования различных технических систем, а также на этапах проектирования, в момент, когда техническая система отсутствует.
Целью данной работы является разработка математической модели захвата руки робота манипулятора. Данный элемент робота должен обеспечивать возможность захвата и удержания объектов.
Для позиционирования детали во время различных производственных операций используется промышленный робот. Промышленный робот предназначен для выполнения двигательных и управляющих функций в производственном процессе, т. е. он представляет собой автоматическое устройство, состоящее из манипулятора и перепрограммируемого устройства управления, которое формирует управляющие воздействия, задающие требуемые движения исполнительных органов манипулятора [1].
Основными узлами, которые входят в комплекс робота, являются:
− система управления;
− система позиционирования изделия;
− система подачи изделия;
− манипулятор: рука робота [2].
При расчете необходимого усилия двухшарнирного захвата с V-образными губками используется метод анализа действующих сил для детали весом G при четырех видах перемещений.
При одновременном торможении всех трех движений:
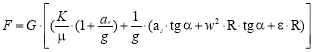 .(1)
.(1)
По этой последней зависимости рассчитывается привод ЗУ.
По данным уравнения (1) была построена имитационная модель реализованная в пакете Simulink прикладных программ MATLAB, модель представлена на рисунке 1.
При построении модели учтем, что угол скоса губок α равен 45°, коэффициент трения равен 0,3 и коэффициент запаса составляет 1,5.
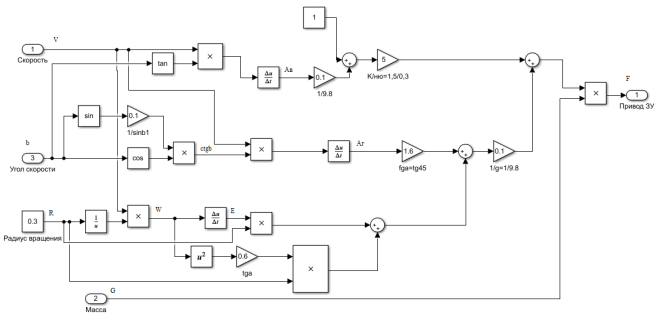
Рис. 1. Модель процесса управления приводом ЗУ
Данная модель служит для проведения расчетов в условных единицах. Результатами моделирования является график изменения усилия захвата в зависимости от изменения массы заготовки, скорости, угла перемещения.
Результаты экспериментов с построенной моделью
Для проверки качества построенной модели проведем ряд экспериментов.
Результатами моделирования будут графики, иллюстрирующие изменения массы, скорости, угла перемещения и усилия захватного устройства.
Проведем эксперименты.
Масса заготовки составляет 15 у.е.; скорость изменяется синусоидально с амплитудой 1, частотой 0,3 радиана в секунду; угол перемещения постоянный и равен 20.
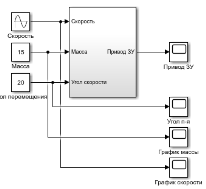
Рис. 2. Имитационная модель эксперимента № 1
График изменения скорости представлен на рисунке 3.
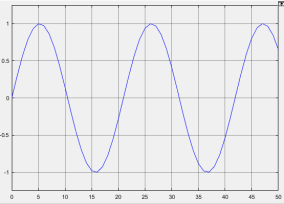
Рис. 3. График изменения скорости перемещения ЗУ
График изменения услилия захватного устройства представлен на рисунке 4. Наибольшего значения усилие достигает в момент максимального ускорения.
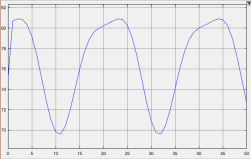
Рис. 4. Изменение усилия привода
Во втором эксперименте масса заготовки составляет 15 у.е.; скорость постоянная и равна 0,1; угол перемещения постоянный и равен 20, масса изменяется по линейному закону.
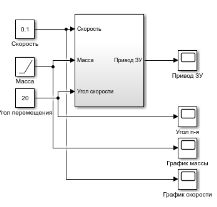
Рис. 5. Имитационная модель эксперимента № 2
График изменения массы представлен на рисунке 6.
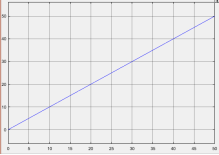
Рис. 6. График изменения угла перемещения
График изменения услилия захватного устройства представлен на рисунке 7. Зависимость усилия привода от изменения массы прямопропорциональная.
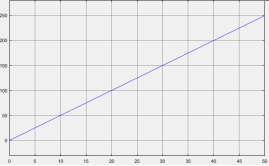
Рис. 7. Изменение усилия привода
По результатам эксперимента видно, что наибольшее усилие захватного устройства необходимо в момент развития максимальной скорости перемещения захвата. В момент времени, когда скорость равняется 0 — усилие заватного устройства минимальное. В то же время, наибольшее усилие захвата возникает в случае, когда угол перемещения практически равен 0 °С — то есть за захват перемещается горизонтально.
Литература:
1 Поезжаева Е. В.; Промышленные роботы: учебное пособие, часть 3. — Пермь: Пермский Государственный Технический Университет, 2009. — 163 с.
2 Устройство промышленных роботов. [Электронный ресурс]. URL: https://studref.com/478180/tehnika/ustroystvo_promyshlennyh_robotov — (Дата обращения: 27.03.19).







