Рассматривается интегральное уравнение Фредгольма первого рода. Такие уравнения встречаются в задачах математической физики (например, в оптических явлениях), в задачах об издержках производства и т. д. Рассматривается частный случай разложимого ядра по базису. Отмечается, что при выполнении некоторых условий решение определяется единственным образом; находится это решение. Результат иллюстрируется примерами.
Ключевые слова: интегральное уравнение Фредгольма, первого рода, решение.
1. Решение уравнения
Рассматривается уравнение
![]() (1)
(1)
где ![]() ,
, ![]() — заданные непрерывные по совокупности переменных функции,
— заданные непрерывные по совокупности переменных функции, ![]() — искомая непрерывная функция;
— искомая непрерывная функция; ![]() .
.
Многие задачи математической физики приводят к таким уравнениям: например, задача восстановления размытого изображения [1]; задача об издержках производства [2] и т. д.
Определение. Вронскианом функций ![]() называется определитель [3]
называется определитель [3]
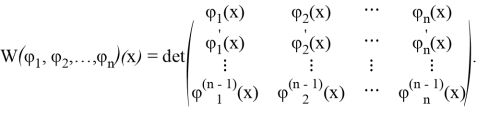
Пусть выполнены следующие условия:
1) ядро
2) ![]() (2)
(2)
3) вронскиан на ![]()
![]() (3)
(3)
4) функция ![]() записывается в виде разложения по тому же базису:
записывается в виде разложения по тому же базису:
![]() (4)
(4)
с постоянными ![]() .
.
Замечание. Подставив выражение (2) для ядра в левую часть уравнения (1), получим выражение вида (4).
Решение уравнения (1) найдем в виде
![]() (5)
(5)
где постоянные ![]() надлежит вычислить.
надлежит вычислить.
Подставив выражения (2), (4) в (1), получим равенство:
![]() (6)
(6)
Приравняв коэффициенты в (6) при ![]() :
:
![]() (7)
(7)
и подставив (5) в (7), получим систему для определения![]() :
:
![]()
![]() (8)
(8)
![]()
![]()
в обозначении
![]() (9)
(9)
Построим следующие матрицы:
![]()

Коэффициенты ![]() в (5) определяются из системы (8) единственным образом, поскольку в силу неравенства (3) имеем
в (5) определяются из системы (8) единственным образом, поскольку в силу неравенства (3) имеем ![]() . Они вычисляются по формулам Крамера [4]:
. Они вычисляются по формулам Крамера [4]:
![]() (10)
(10)
Таким образом, получен следующий результат.
Теорема. При выполнении условия (3) решение уравнения (1), (2), (4) единственно и определяется по формулам (5), (10), (9).
2. Примеры
Пример 1. Решить уравнение
![]() (11)
(11)
1) Ядро ![]() и функцию
и функцию
![]()
![]()
2) Проверим, что выполнено условие (3). Действительно, на ![]()
![]()
3) Проверим, что функции ![]() ,
, ![]() образуют базис на
образуют базис на ![]() . Действительно,
. Действительно,
![]()
4) Тогда в силу теоремы решение уравнения (11) единственно и равно
![]() (12)
(12)
где по формулам (10), (9)
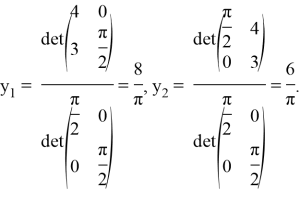
Непосредственной подстановкой выражения (12) в уравнение (11) убеждаемся в правильности решения.
Пример 2. Решить уравнение
![]() (13)
(13)
1) Внесем интегралы в левой части уравнения под один интеграл. Ядро ![]() и функцию
и функцию ![]() можно представить в виде (2) и (4), где
можно представить в виде (2) и (4), где
![]()
![]()
![]()
2) Проверим, что выполнено условие (3). Действительно, на ![]()
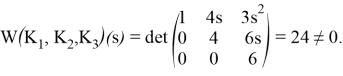
3) Проверим, что функции ![]() ,
, ![]() ,
, ![]() образуют базис на
образуют базис на ![]() . Действительно,
. Действительно,
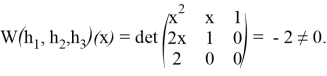
4) Тогда в силу теоремы решение уравнения (13) единственно и равно
![]() (14)
(14)
где по формулам (10), (9)
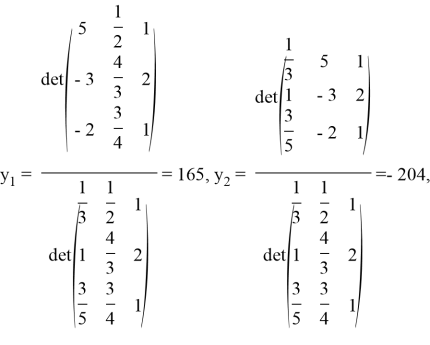
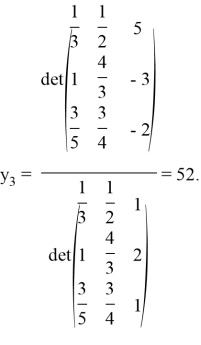
Непосредственной подстановкой выражения (14) в уравнение (13) убеждаемся в правильности решения.
Литература:
- Полянин А. Д., Манжиров А. В. Справочник по интегральным уравнениям. М.: Физматлит, 2003. — 608 с.
- Спирина М. С., Спирин П. А. Интегральные уравнения при моделировании издержек // Вестник Поволжского госуниверситета. Серия: Экономика. — 2015. — № 2 (40). — С. 234–238.
- Понтрягин Л. С. Обыкновенные дифференциальные уравнения. М.: Наука, 1974. — 331 с.
- Гельфанд И. М. Лекции по линейной алгебре. М.: Добросвет, МЦНМО, 1998. — 320 с.
- Выгодский М. Я. Справочник по элементарной математике М.: 2006. — 509 с.







