В статье рассматривается важная для практики задача о пуске скважины с постоянным дебитом, при фильтрации в пласте вязкопластичной жидкости с предельным градиентом давления. Задача решена методом «усреднений» для одномерного поступательного потока упругой жидкости [1,2].
Ключевые слова: приближенный, одномерно поступательный, упругий, начальный градиент, метод «усреднений».
The article considers an important practical task of starting a well with a constant flow rate when filtering a viscoplastic fluid in a reservoir with a limiting pressure gradient. The problem is solved by the method of «averaging» for a one-dimensional translational flow of an elastic fluid [1,2].
Key words: approximate, one-dimensionally translational, elastic, initial gradient, method of “averaging”.
В задаче предполагается, что пласт одномерный, начало координат расположено у галереи, а ось х направлена по длине пласта.
Согласно предположению. соответствующее уравнение имеет вид:
![]() (1)
(1)
Заменим уравнение (1) приближенным уравнением:
![]() (2)
(2)
где
![]() (3)
(3)
Также предположим, что задан дебит галереи во времени, приходящийся на единицу ширины поперечного сечения ![]() :
:
Интегрируя выражение (1), получаем:
![]() (4)
(4)
или ![]() (5)
(5)
Граничные условия для данной задачи запишем в следующем виде:
![]() при
при ![]() (6)
(6)
![]() при
при ![]() (7)
(7)
![]() при х = 0 (8)
при х = 0 (8)
Учитывая условие (6) в (4) получаем:
Откуда получаем: ![]() (10)
(10)
Используя (10) и (4) в (8) получаем:
![]() (11)
(11)
и ![]() (12)
(12)
Подставляя (12) в (11) имеем:
![]() (13)
(13)
Если интегрируем уравнение (13) получаем выражение:
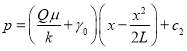 (14)
(14)
Учитывая условие (7) в (14) получаем:
![]()
или
![]() (15)
(15)
Если учесть (15) в (14) то получаем:
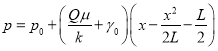 (16)
(16)
В (16) учитывая, что ![]() и
и ![]() определяем
определяем ![]() :
:
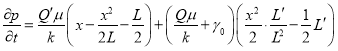
Определим ![]() из (3). Тогда
из (3). Тогда
![]() (17)
(17)
Приравнивая правые части уравнений (12) и (17) получаем:
![]() (18)
(18)
Для решения этого дифференциального уравнения умножим обе части на ![]() . Тогда получаем:
. Тогда получаем:
После несложных преобразований получаем:
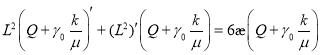
или
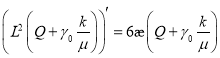 (20)
(20)
Интегрируя последнее уравнение, имеем:
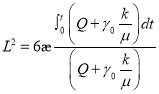 (21)
(21)
В частности, при постоянном дебите мы получаем известную формулу [1]
![]() (22)
(22)
Таким образом, получена формула для определения границы возмущения при одномерном поступательном движении упругой жидкости (21).
Если подставить ![]() в (14) получим закон распределения давления. И если (21), (13) учесть в (8) получим дебит галереи.
в (14) получим закон распределения давления. И если (21), (13) учесть в (8) получим дебит галереи.
Литература:
- Г. П. Гусейнов. Некоторые вопросы гидродинамики нефтяного пласта. Азербайджанское государственное издательство. Иаку-1961, 232 с.
- Подземная гидравлика. Учебник для вузов./ К. С. Басинов, А. М. Власов, И. Н. Кочина, В. М. Максимов.-М.:Недра, 1986–303 с.







