В данной статье выполнены численные сравнения напряженно-деформированного состояния арки из тонкостенных вальцованных профилей системы MIC-120 и арки с приведенным Т-образным сечением при загружении различными видами нагрузок.
Ключевые слова: вальцованный U-образный профиль системы MIC-120, ветровая нагрузка, гидростатическое давление, гравитационная нагрузка, арка, свод, приведение эквивалентного поперечного сечения, компьютерное моделирование.
Если необходимо моделировать свод в пространстве, при наличии торцевых диафрагм или сложных граничных условиях свода, то нужно задавать оболочку, моделировать оболочку в натуральном виде из вальцованных профилей свода не представляется возможным. Сравним напряжения и перемещения в арках из гофрированного U образного и гладкого Т образного сечений.
Цель: численные сравнения напряженно — деформированного состояния арки из тонкостенных вальцованных профилей системы MIC-120 и арки с приведенным Т-образным сечением при загружении различными видами нагрузок.
Материалы иметоды:
Смоделируем твердотельно в программном комплексе Solid Works арочный вальцованный профиль U образного сечения и арочный гладкий профиль Т образного приведенного сечения пролетом 15,24м. для сравнения напряженно — деформированных состояний в арки [1], [3]. Формы поперечных сечений показаны на рисунке 1. Приведенное Т-образное — эквивалентное сечение с известной редуцированной площадью А и известным редуцированным моментом инерции J определим в соответствии с методикой перехода от U образного сечения к Т образному сечения рассмотренном ранее в статье [3]. Редуцированный момент инерции и площадь получены численными вычислениями, твердотельным моделированием [3]. Арочные профили были рассчитаны методом конечных элементов и выявлены распределения напряжений и перемещений при следующих постоянных видах загружений: ветровое, гравитационное, гидростатическое давление и сосредоточенная нагрузка.
Для определения напряжений и перемещений арочного профиля использовали модель пролетом 15,4м толщиной листа профиля гофрированного профиля 1мм, в виде двухшарнирной статически неопределимой арки [1]. Закрепляем связями стенки профилей из плоскости изгиба, учитывая, что в реальных конструкциях сводов соседние стенки профилей сцеплены и сдерживают друг друга. Поочередно загрузим арку ветровым, гравитационным, гидростатическим давлениями и сосредоточенной нагрузкой в коньке. Загружения приложены к гофрированной полке профилей. Результаты вычислений по напряжениям и перемещениям в арках представлены цветовой графикой на рис. 1–4.

Рис. 1. Распределение напряжений в гофрированном профиле при гравитационной нагрузке на арку пролетом 15.24м t=1мм
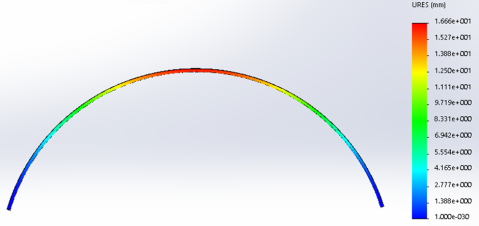
Рис. 2. Эпюра перемещений гофрированного профиля при гравитационной нагрузке на арку пролетом 15.24м t=1мм
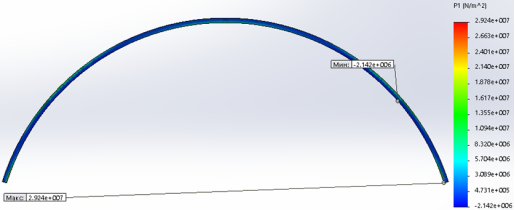
Рис. 3. Распределение напряжений в приведенном Т образном профиле при гравитационной нагрузке на арку пролетом 15.24м
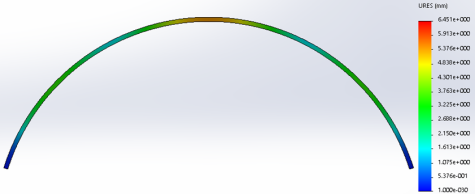
Рис. 4. Эпюра перемещений приведенного Т образного профиля при гравитационной нагрузке на арку пролетом 15.24м
Таблица1
|
Вид нагрузки |
Результаты расчета ввальцованном профиле U |
Результаты расчета вприведенном Тобразном профиле |
|
||||||
|
δ, мм |
σmax, Н/м2 |
σmin, Н/м2 |
δ, мм |
σmax, Н/м2 |
σmin, Н/м2 |
|
|
|
|
|
Гравитационная |
16,7 |
9,8e+7 |
-6,6e+6 |
6,5 |
2,9e+7 |
-2,14E+6 |
2,59 |
3,34 |
3,1 |
|
Радиальная |
0,26 |
1,14e+7 |
-2,4e+6 |
0,54 |
1,01e+6 |
-1,29e+5 |
0,49 |
11,3 |
18,44 |
|
Ветровая |
0,31 |
7,2e+6 |
-4,4e+5 |
16,1 |
1,15e+8 |
-9,93e+6 |
0,02 |
0,06 |
0,044 |
|
Сосредоточенная |
1,14 |
-1,0e+8 |
-1,06e+7 |
57 |
4,61e+8 |
-3,65e+5 |
0,02 |
-0,22 |
28,95 |
Результаты: Исходя из результатов по главным напряжениям и перемещениям получены коэффициенты условий работы вальцованной конструкции, необходимые также для проверки нормативных ограничений (понижающие/повышающие коэффициенты условий работы) по максимальным/минимальным напряжениям и перемещениям (они представлены в таблице 1) [4]. Коэффициент для перемещений вычислен для сравнения перемещений, полученных при натурных испытаниях свода с результатами перемещений, полученных численным расчетом модели оболочки с приведенным сечением.
Литература:
- Карабутов М. С. Твердотельное моделирование тонкостенных вальцованных профилей металлических сводов// Материалы международной научно-практической конференции «Строительство-2008», -Ростов н/Д: Рост. гос. строит. ун-т, -2008. -С. 55.
- Веселев Ю. А., Карабутов М. С. Экспериментальное изучение поведения свода из вальцованных металлических тонкостенных профилей при действии ветра и сравнение полученных результатов с результатами компьютерного моделирования обдувания свода ветром// Строительная механика инженерных конструкций и сооружений. -2012. — № 2. –С. 72–77.
- Веселев Ю. А., Карабутов М. С. Приведение вальцованного U-образного профиля с редуцированными жесткостными характеристиками к гладкому тавровому профилю. // Строительная механика инженерных конструкций и сооружений. -2012 год. № 1, -С.30–37.
- Веселев Ю. А., Карабутов М. С. К вопросу о надежности тонкостенных металлических сводов из вальцованных профилей//«Строительство-2013» «Современные проблемы промышленного и гражданского строительства» «материалы международной научно-практической конференции». -Ростов н/Д: Рост. гос. строит. ун-т, 2013. -43с.







