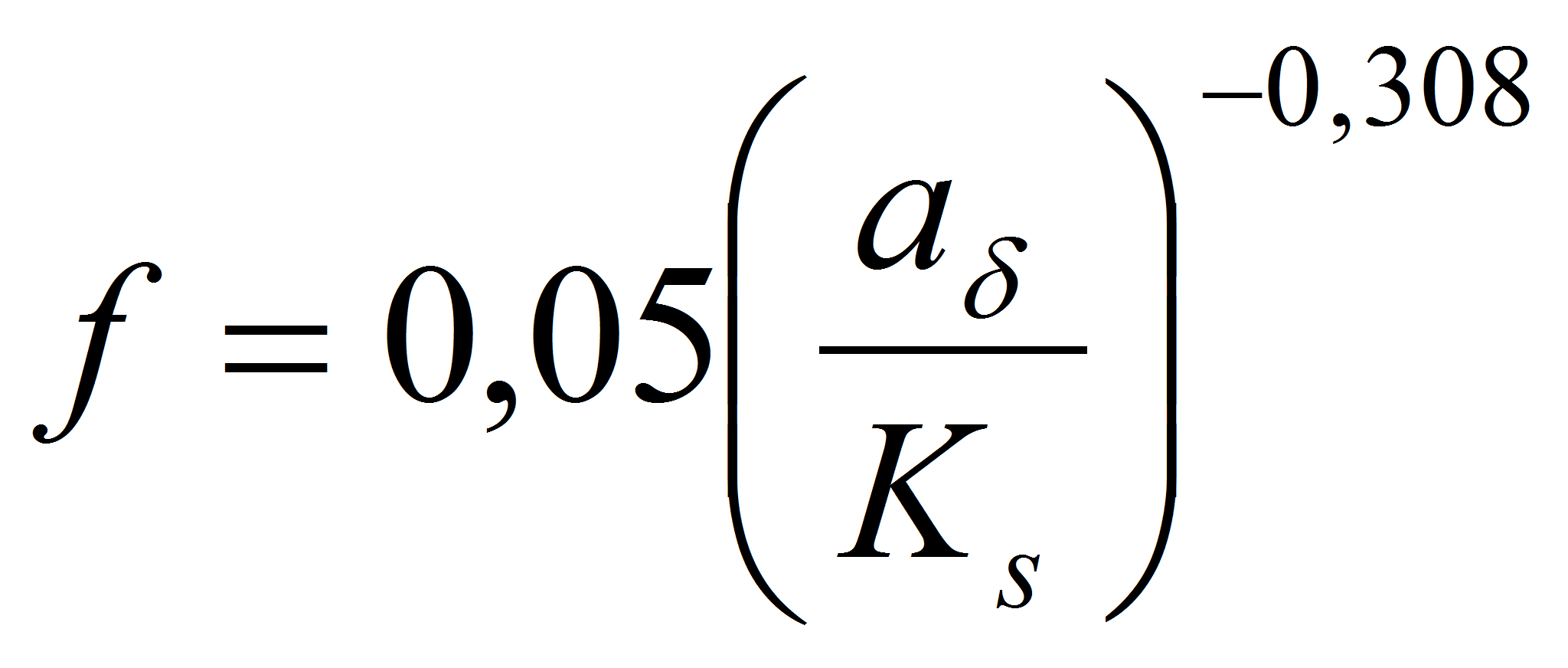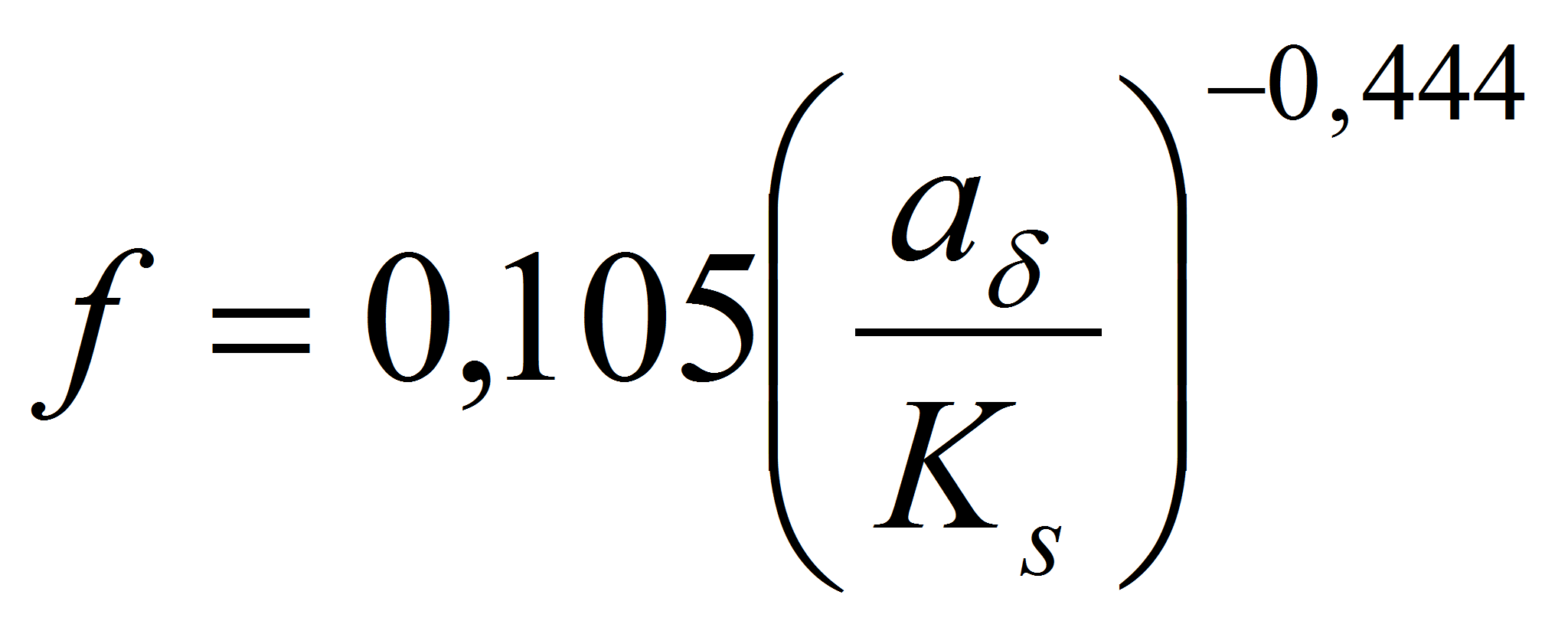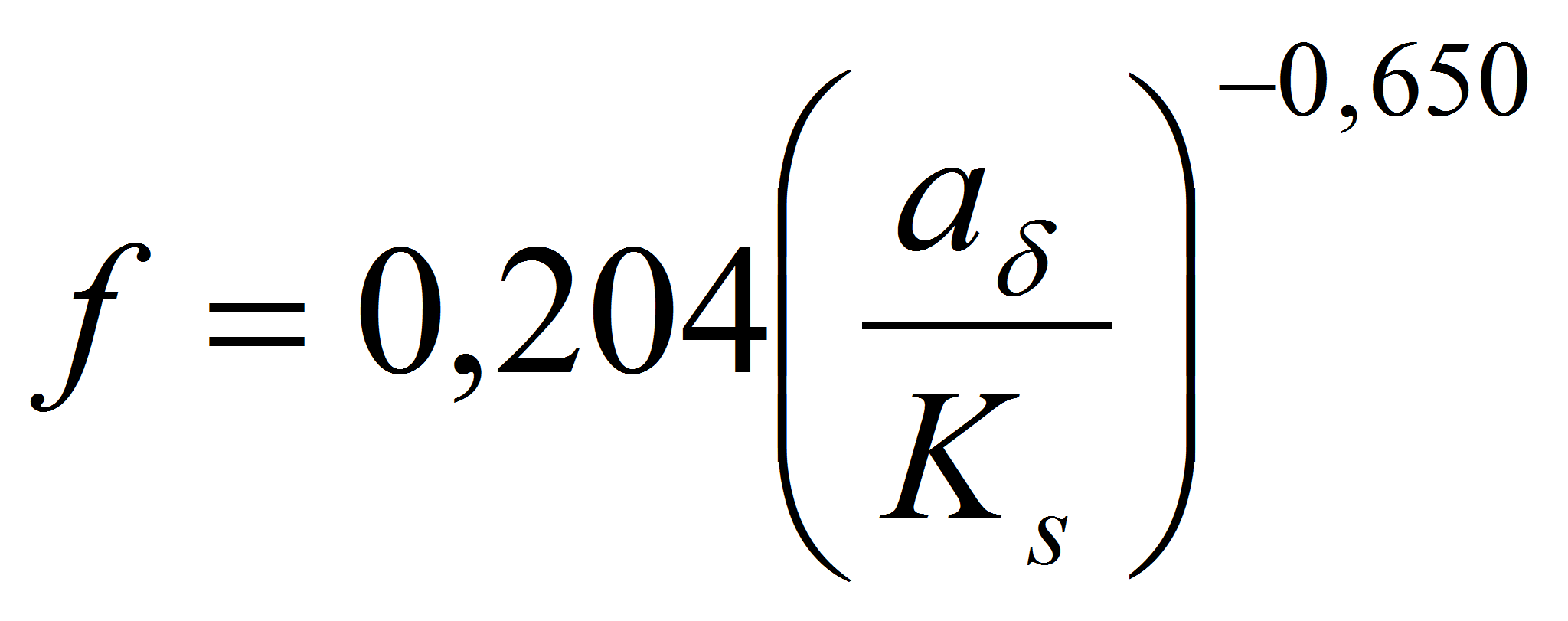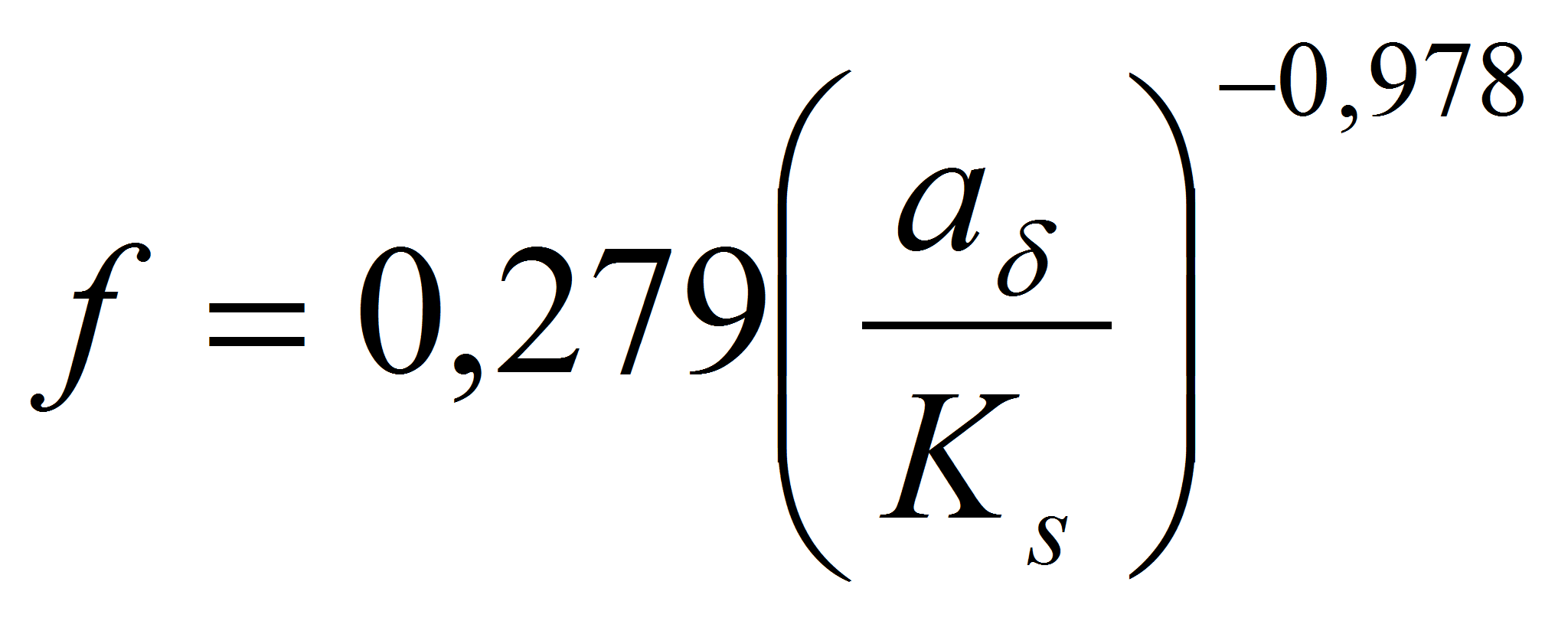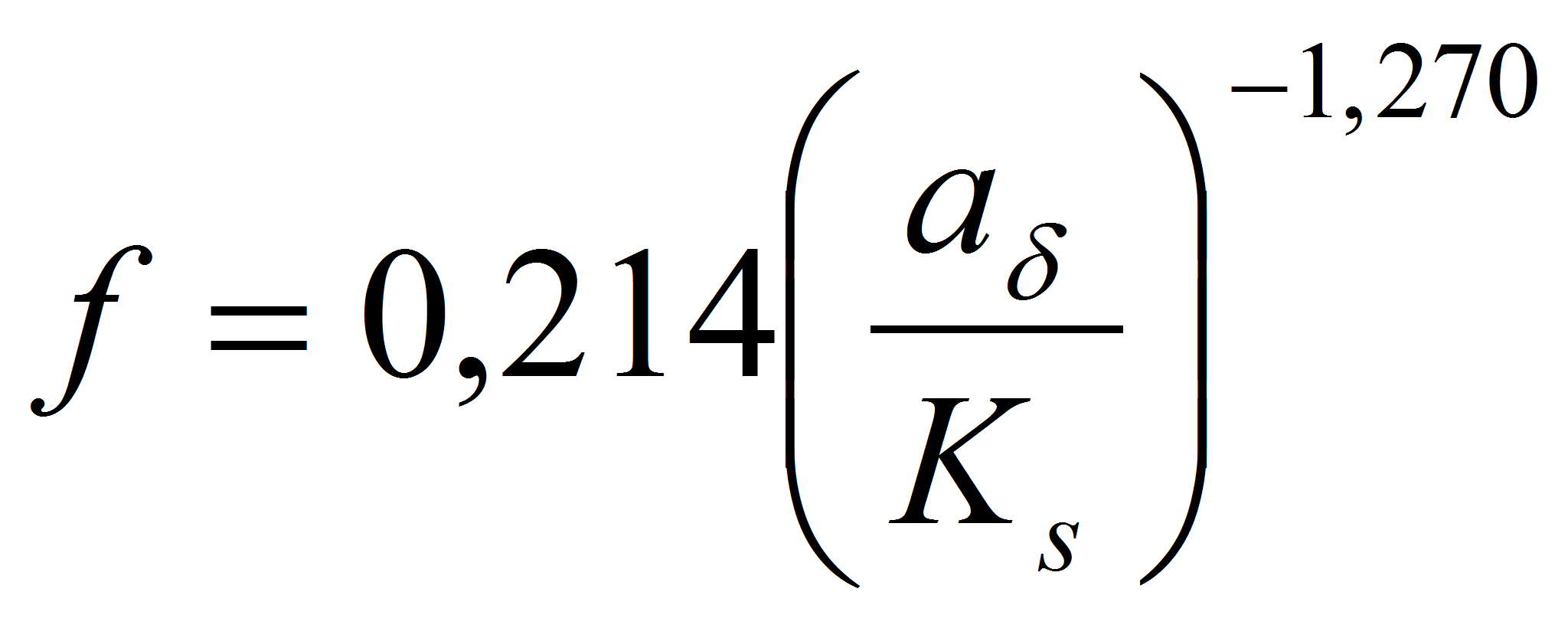При решении проблем, связанных, с прогнозом транспорта наносов при наличии различного рода волновых движений, ведущее место занимает вопрос о формировании нестационарного турбулентного пограничного слоя. Поэтому не случайно исследование эрозионных процессов, обусловленных волновыми потоками в большинстве случаев начинается с изучения структурных особенностей пограничного слоя, которые в естественных условиях имеют преимущественно турбулентный характер. В настоящее время, благодаря фундаментальным исследованиям целого ряда авторов [1,2] в области исследования пограничного слоя достигнуть достаточно большие успехи. Однако, в виду больших математических трудностей описания процесса формирования пограничного слоя в условиях колебательного (осциллирующего) характера движения, на современном этапе, по-прежнему, существуют занимательные пробелы и прежде всего, в области достоверной количественной оценки параметров нестационарных слоев, которая во многом определяет правильность принятия проектных решений при гидротехническом строительстве.
Существующие математические модели пограничного слоя в большинстве случаев основываются на уравнениях, полученных после ряда упрощений общей системы уравнений Навье- Стокса и имеют вид:
(1)
(2)
где
,
–
составляющие
вектора скорости в пограничном слое, соответственно, по осям х и z;
р –
давление;
- кинематический
коэффициент
молекулярной
взякости;
–удельная
плотность воды.
Обычно граничными условиями служат:
при
z=о;
при
z
=∞.
(3)
Система (1)-(3) называется уравнениями Прандтля для пограничного слоя.
В нестационарном случае, когда движение имеет колебательный, осциллирующий характер, и необходим учёт возникающих при больших числах Pейнольдса турбулентных пульсаций, система (1)-(3) видоизменяется.
(4)
(5)
Граничные условии:
при
при
,
(6)
где
-
кинематический
коэффициент турбулентной взякости;
уровень
нулевых
скоростей;
Кs-
высота
эквивалентной шероховатости
по Никурадзе;
-толщина
пограничного подслоя.
скорость
невязкого
внешнего течения,
связанная
с давлением в пограничном слое соотношением:
(7)
Объединяя (4) и (7) получаем основную систему уравнений, описывающую движение в нестационарном пограничном турбулентном слое:
(8)
(9)
В большинстве случаев, учитывая незначительные вертикальные размеры пограничного слоя и малую роль вблизи дна нелинейных членов, система (8)-(9) приводится к виду:
(10)
(11)
В таком (или подобном) виде система анализировалась целым рядом исследователей. В качестве недостатков большинстве существующих теорий можно отметить следующие:
1) они не учитывают нестационарности коэффициента турбулентной вязкости;
2) толщина пограничного слоя принималась в виде независимой от времени величины.
3) изменение тангенциального напряжения принималось синусоидальным.
Не
вдаваясь математические тонкости существующих моделей пограничного
слоя следует отметить следующее. В каждой из теоретических разработок
предпринимались попытки (более или менее удачная) получения
зависимости для наиболее важной с точки зрения транспорта наносов
величины – параметра трения
(здесь
-максимальное
значение
динамической скорости
в волновом потоке,
–максимальное
значие орбитальной скорости на внешнем
крае
турбулентного пограничного слоя).
При этом в ряде случаев,
исследователями
удавалось
получить зависимости,
находящиеся
в довольно хорошем соответствии с экспериментальными, данными
(рис.1).
Однако это соответствие, на
наш взгляд, является недостаточным для разработки достоверных методов
прогноза транспорта наносов при волнениях. Поэтому целью нашей работы
явилось обобщение существующих лабораторных и натурных данных для
получения достаточно надежной эмпирической зависимости для расчёта
параметра трения, включающего важнейшую для решения проблемы
транспорта наносов в волновых потоках
.
Рис.1. График связи f=fct(a&#;/Ks). 1 – связь [5], 2 – связь [6].
В результате анализа
современной литературы [3] получены данные 51 измерений изменения
параметра
и
(где
).
По данным этих измерений построена зависимость f=fct(a&#;
/Ks),
представленная
на рис.1,
которая выгодно
на наш взгляд,
отличается
от полученных
ранее аналитических
связей. Для удобства практического использования полученной
эмпирической
связи она была аппроксимирована с точностью до 2 % серией
зависимостей в виде:
(11.a)
(11.б)
(11.в)
(11.г)
(11.д)
Зависимости (11а)-(11д) можно использовать в расчётах транспорта наносов и эрозионных процессов в условиях ветрового волнения, а также при исследовании нестационарной теплопередачи и гидродинамического сопротивления в подземных вентиляционных каналах плодоовощехранилищ.
- Литература:
1. Лойцянский Л.Г. Механика жидкости и газа. – М.: Наука, 1970. – 904 с.
2.Шлихтинг Г. Теория пограничного слоя. – М.: Наука, 1974. – 711 с.
3. Михинов А.Е., Эшев С.С. Расчёт параметра трения в условиях нестационарного турбулентного пограничного слоя. – М.: 1987. – 9 с. Деп. в ВИНИТИ. 17.11.87, №8088-В87.
4.Jonsson I.G., Carlsen N.A. Experimental and theoritikal investigations in an oscillatory turbulent boundary layer. - J. hydraul. Res., vol. 14, - №1, 1976. - р.45-60.
5.Kajiura K. A model of the botton boundary layer in water waves. Bulliten of the Eartquake Research Institute, Vol. 46, 1968. - р. 75-123.
