- Действие алгоритма основано на учете величины момента
сопротивления. Привод совершает разгибательное движение в суставе до
тех пор, пока сопротивление не достигнет порогового значения Мкр.
В этом случае привод переключается на осциллирующий режим, заставляя
сустав совершать быстрые колебательные движения малой амплитуды.
Такой режим способствует расслаблению сгибательных мышц и снижению
болевых ощущений. Осциллирующий режим функционирует некоторый период
времени (от нескольких секунд до нескольких минут), задаваемый
программно, после чего привод возвращается в исходное положение,
заставляя сустав сгибаться и давая возможность для восстановления
локального кровообращения и релаксации разгибателей. Затем цикл
повторяется вновь.
- В приводе реализован алгоритм управления движением шарнирно-рычажной системы тренажера для разработки контрактур с уменьшением болевых ощущений.
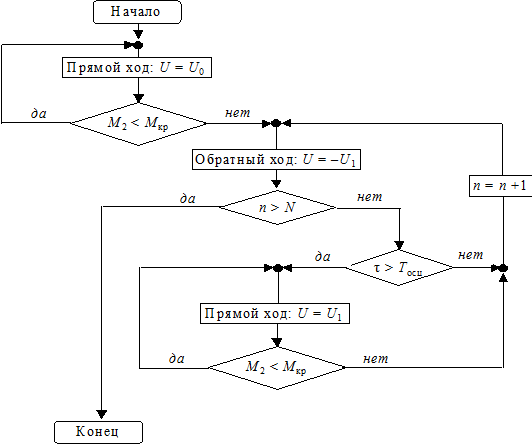
- Схема работы алгоритма в течение одного цикла разработки показана на рис. 1.
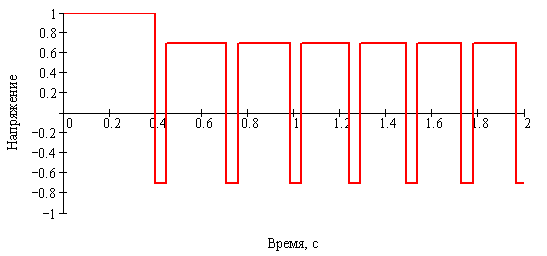
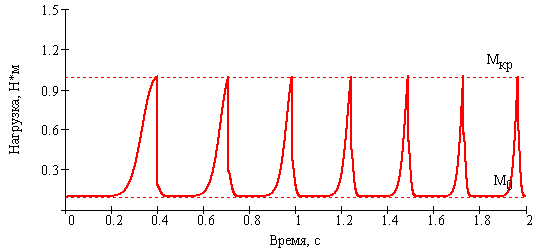
- Алгоритм работает следующим образом. Под действием номинального напряжения U = U0 привод совершает разгибание сустава (прямой ход) до тех пор, пока сопротивление не достигнет критического значения Мкр. Этот момент фиксируется датчиком тока, т.к. потребляемый ток прямо пропорционален преодолеваемой нагрузки:
 , (1)
, (1)- где сМ – отношение статического синхронизирующего момента двигателя к пусковому току фазы.
- При достижении М2 = Мкр происходит переключение на режим осцилляции. Привод под действием управления U = –U1 начинает отрабатывать движение в обратном направлении (сгибание сустава) в течение заданного полупериода осцилляции Тосц. Амплитуда управляющего напряжения U1 определяется из условия прохождения заданного угла разгибания α за полупериод:
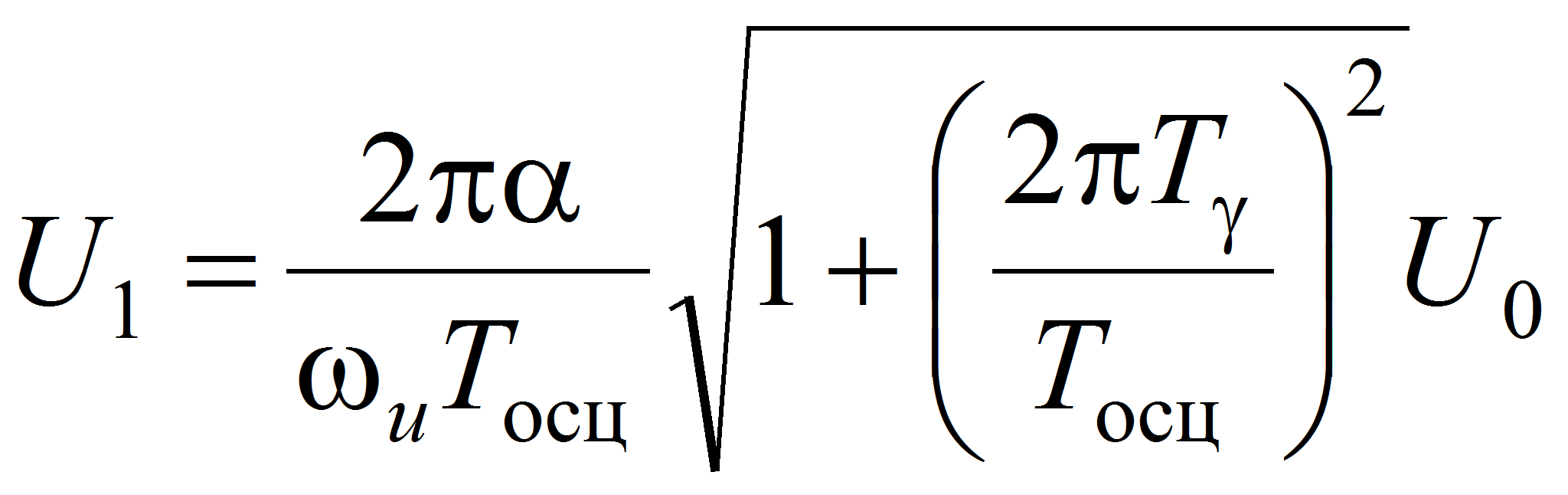 . (2)
. (2)- При окончании полупериода в момент времени τ = Тосц происходит переключение управления на прямой ход U = U1, заставляя сустав разгибаться. Разгибание продолжается до тех пор, пока вновь не наступит событие М2 = Мкр, после чего совершается второй цикл осцилляции.
- В течение каждого колебания в фазу осцилляции счетчик циклов n регистрирует количество совершенных осцилляций. При совершении заданного числа N осцилляций фаза осцилляции заканчивается и привод под действием управляющего напряжения U = –U1 возвращается в исходное положение и цикл разработки заканчивается.
- Для работы алгоритма необходимо задать следующие параметры:
- В приводе реализован алгоритм управления движением шарнирно-рычажной системы тренажера для разработки контрактур с уменьшением болевых ощущений.
-
Мкр – пороговое значение момента
сопротивления, характеризующего наступление контрактуры, Н∙м;
- М – число циклов разработки в течение сеанса разработки;
- N – число осцилляций в течение цикла разработки;
- Тосц – полупериод осцилляции, с;
- α – амплитуда осцилляции, град.
- М – число циклов разработки в течение сеанса разработки;
Рис. 1. Схема работы алгоритма в течение одного цикла разработки
-
Остальные параметры (характеристики двигателя: ωХХ,
МП, Jрот,
U0; редуктора: u,
η, J1, J2;
предельный угол разгибания в суставе φпр) фиксированы
и зашиты в ПЗУ микропроцессора. Их можно также перепрограммировать,
например, при перенастройке тренажера на другой сустав, замене
двигателя или редуктора, но в отличие от перечисленных выше
параметров управления они недоступны через пульт пользователя.
- Для проверки работоспособности предложенного алгоритма проведен комплекс исследований по имитационному моделированию динамики тренажера.
- Заметим, что для работы алгоритма не важен точный вид зависимости (6) и тем более значение показателя контрактуры (который существенно привязан к предложенной модели). Но для имитационной модели необходимо формализованное описание зависимости усилия сопротивления разгибанию от угла разгибания, причем с учетом положительной динамики в процессе разработки.
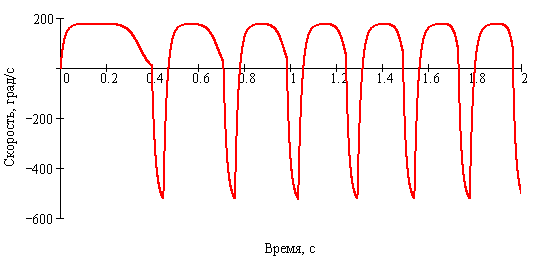
- На рис. 2–6 представлены результаты имитационного моделирования: показаны диаграммы изменения угла и угловой скорости разгибания, управляющего напряжения, момента сопротивления и показателя контрактуры за цикл разработки. Для наглядности предложен идеализированный случай, когда каждая осцилляция эффективна – после каждой осцилляции показатель степени 1/k в выражении (6) увеличивается на единицу. Режим осцилляции – Тосц = 0,1 с, α = 20º. Подвижность в суставе до начала разработки составляла 56,1º, в конце цикла разработки – 80,1º. Можно видеть, что обратный ход начинается в момент, когда М2 = Мкр.
- Прямой ход в течение каждой осцилляции совершается за большее время, чем обратный. Это связано с тем, что во время прямого хода приводу приходится преодолевать сопротивление, тогда как в течение обратного хода нагрузка помогает тренажеру сгибать сустав.
- Основным результатом проведенного моделирования является проверка работоспособности алгоритма. Построенная на диаграммах реализация подтверждает, что алгоритм обеспечивает требуемый режим осцилляции.
- Для проверки работоспособности предложенного алгоритма проведен комплекс исследований по имитационному моделированию динамики тренажера.
|
Рис. 2. Диаграмма изменения угла разгибания за цикл разработки |