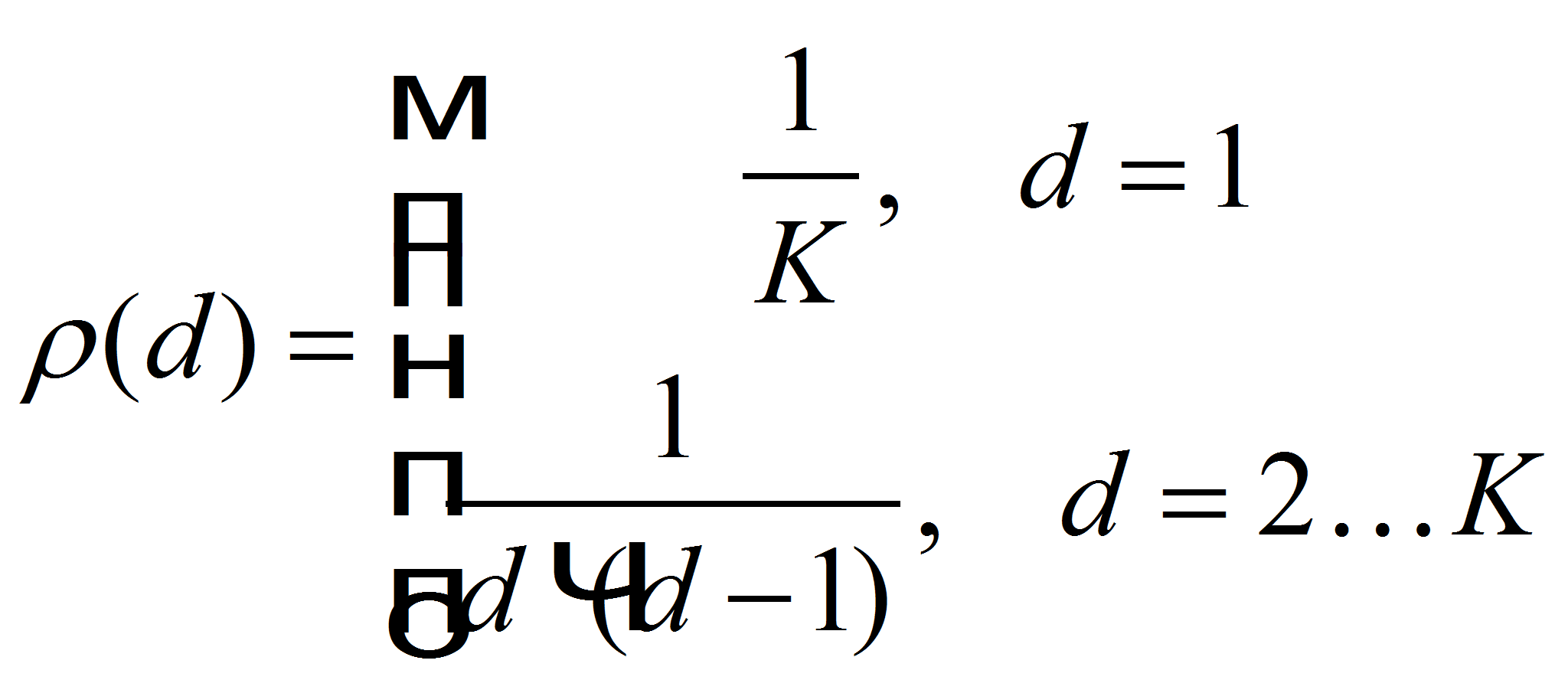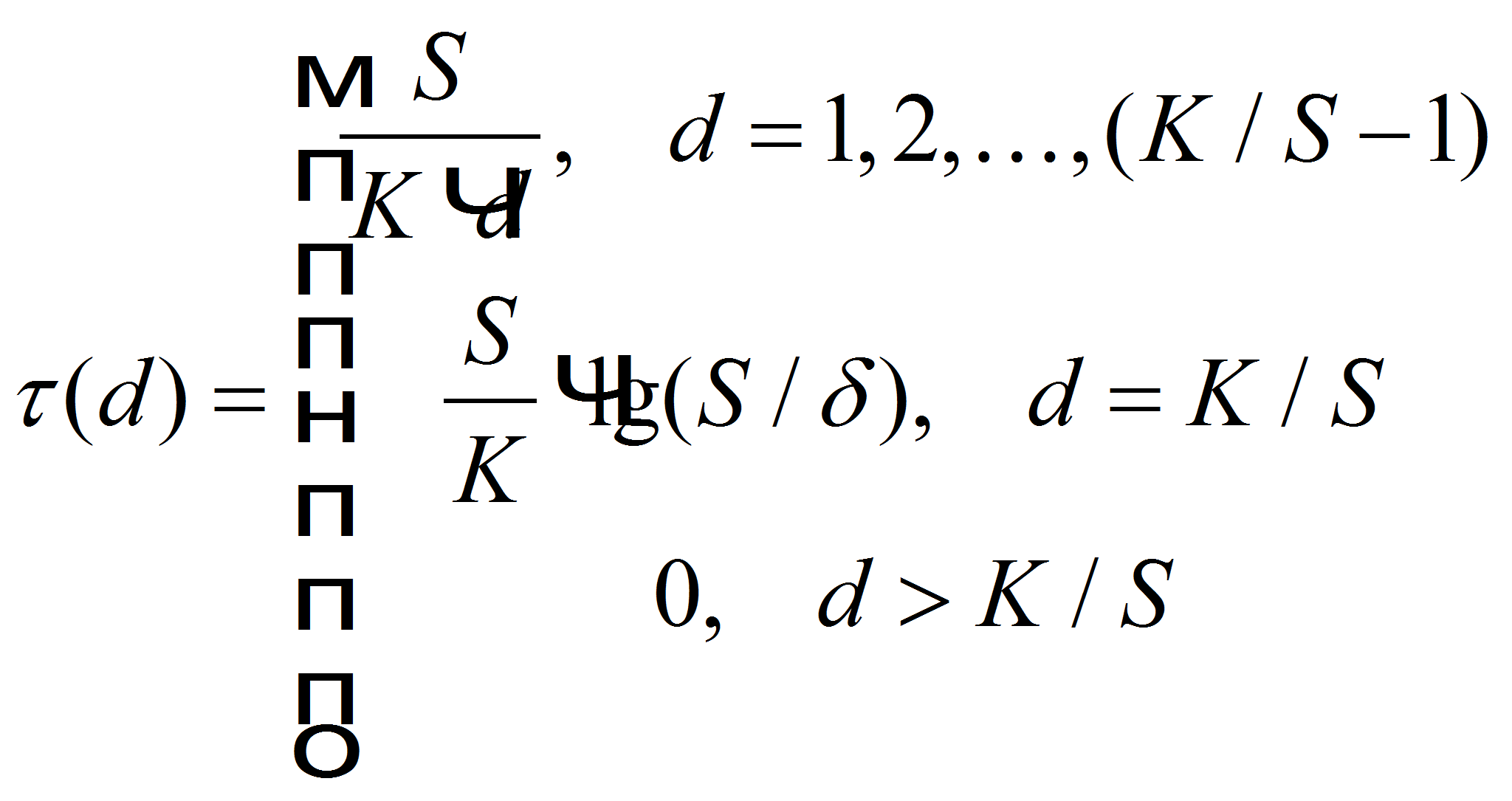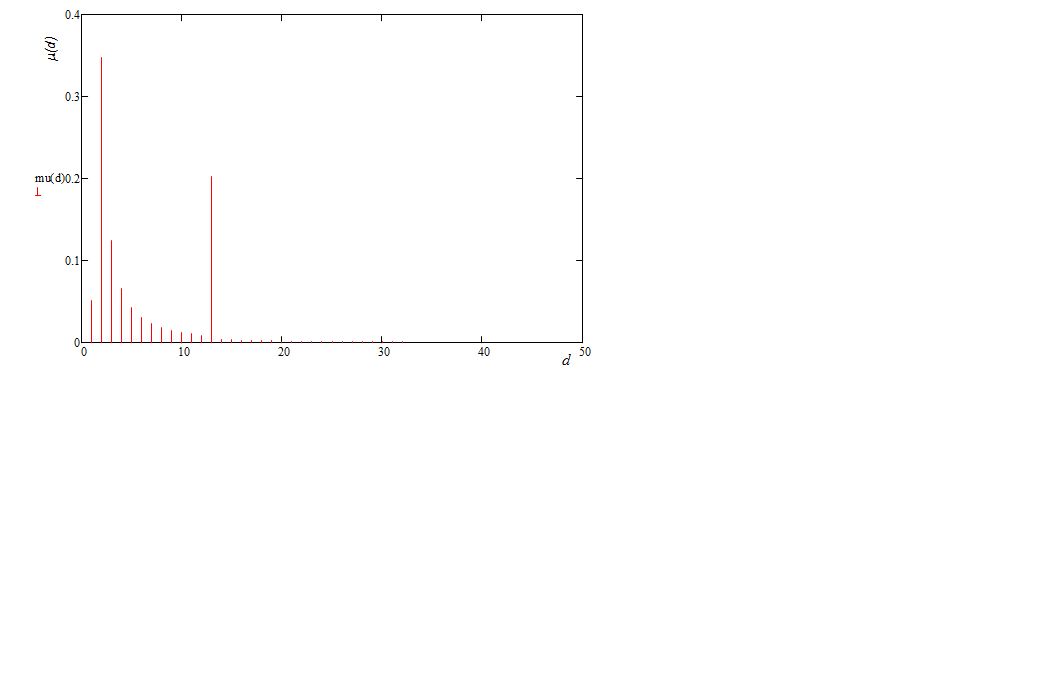Представлены основные теоретические аспекты построения LT-кодов. Разработана имитационная система передачи данных с использованием помехоустойчивых кодов LT, позволяющая оценить возможности использования данной идеологии. Представлены основные результаты моделирования, подтверждающие эффективность кода.
В последнее время существует тенденция стремительного увеличения объема передаваемой информации в пакетных сетях передачи данных. В действующих пакетных сетях, как правило, используются два способа передачи информации: дейтаграмный (посредством протокола транспортного уровня UDP), который вносит минимальные задержки, но при этом, не гарантируя качества передачи, и метод с установлением соединения на транспортном уровне (протокол TCP), обеспечивающий требуемое приложением качество передачи информации, однако, при этом значительно увеличиваются задержки. Существуют случаи, когда требуется точность принятия сообщения при ограничении допустимых задержек. При этом размер передаваемых блоков может быть достаточно большим (например, блоки IP-TV). Для решения подобных задач был предложен класс кодов со стираниями (erasure codes) [1]. В данной работе представляется модель системы передачи данных, использующая коды LT (Luby transform), разработанная в среде Simulink.
Впервые коды LT
представлены в работе [1]. Ключом
к пониманию LT
кодов является описание процесса кодирования. Допустим, имеется
сообщение из K
![]() информационных
пакетов, причем размеры всех пакетов одинаковы. Каждый кодовый пакет
получается из исходных информационных следующим образом:
информационных
пакетов, причем размеры всех пакетов одинаковы. Каждый кодовый пакет
получается из исходных информационных следующим образом:
Случайным образом выбирается dn степень пакета из функции плотности распределения степени µ(d) (подробно рассмотрена ниже).
Из К информационных пакетов случайно выбирается dn - соседи.
Производится побитное сложение пакетов-соседей по модулю 2 (XOR), результатом данной операции будет являться кодовый пакет tn.
Отметим, что, кроме самих кодовых символов, в пакетах должна содержаться информация о соседях, включенных в текущий кодовый пакет.
Для полного понимания работы кода рассмотрим процесс декодирования, который заключается в следующем:
Выбирается кодовый пакет tn со степенью dn равной 1 (если такого пакета нет, то процесс декодирования прерывается на данном шаге). Кодовый элемент, имеющий единичную степень, ввиду специфики кода будет аналогичен исходному информационному элементу si (информация о нем, как уже отмечалось ранее, содержится в tn).
Операцией XOR удаляем элемент si из всех кодовых пакетов, где он присутствует, при этом понижая степень кодовых пакетов, соответственно, на 1.
Возвращаемся к шагу 1.
Для уверенного декодирования важную роль играет функция плотности распределения степени кодового пакета. Если на каком-то из шагов декодирования не будет ни одного элемент с единичной степенью, то процесс автоматически завершить на данном этапе и оставшиеся кодовые пакеты не будут декодированы.
В идеальном случае для декодирования достаточно иметь хотя бы 1 кодовый пакет единичной степени и достаточное число элементов степени 2. Согласно этой идеологии построено идеальное Солитоновское распределение (Ideal Soliton distribution). Идеальным Солитоновским распределением называется распределение, плотность распределения вероятности которого задается:
Однако, на практике идеальное распределение дает плохие результаты. Для обеспечения стабильного декодирования было разработано робастное Солитоновское распределение (Robust Soliton distribution) [1], плотность распределения μ(d) которого задается формулой:
где p(d) определяется согласно (1), а τ(d) (робастное распределение):
Параметр S
введен для того, чтобы удовлетворить вероятность того, что количество
элементов степени 1 d1
≡ S.
Параметр
![]() - граница вероятности того, что процесс декодирования прервется после
принятия K`
пакетов.
Другими словами число кодовых пакетов, необходимых на приемной
стороне для того, чтобы завершить процесс декодирования с
вероятностью
- граница вероятности того, что процесс декодирования прервется после
принятия K`
пакетов.
Другими словами число кодовых пакетов, необходимых на приемной
стороне для того, чтобы завершить процесс декодирования с
вероятностью
![]() ,
,
![]() .
Константа с
выбирается
на практике в диапазоне от 0 до 0.2, хотя может варьироваться до 1.
.
Константа с
выбирается
на практике в диапазоне от 0 до 0.2, хотя может варьироваться до 1.
Робастное Солитоновское распределение имеет два максимума: на d=2 и d=K/S. Кроме того распределение предполагает достаточное количество элементов степени 1. Пример распределения приведен на рисунке 1.
Рис. 1. Робастное Солитоновское распределение δ=0.5, с=0.01, N=1000
Распределение сконструировано таким образом, чтобы увеличить вероятность полного декодирования сообщения. Функция плотности вероятности такова, что в процессе кодирования генерируется достаточное количество элементов единичной степени и, наряду с этим, её максимум приходится на значение степени 2. Это позволяет запустить так называемый процесс «пульсации», который предполагает наличие на каждом последующем шаге хотя бы одного элемента с единичной степенью.
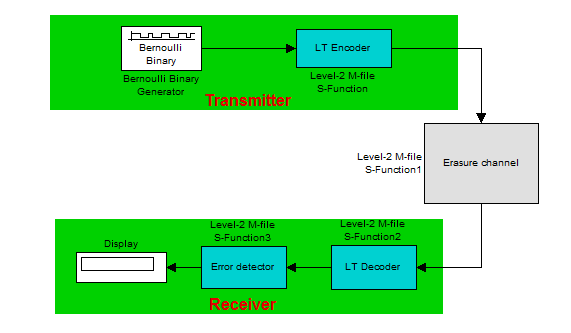
Для исследования возможностей LT-кода была разработана модель системы передачи в среде Simulink. Основные функциональные блоки системы схематично представлены на рисунке 2.
Рис. 2. Модель системы передачи, использующей LT-коды, в среде Simulink
Результаты, полученные с помощью модели, для параметров кода δ=0.5, с=0.01 представлены в таблице 1.
Таблица 1. Результаты имитационного моделирования δ=0.5, с=0.01
|
Избыточность, % |
PLR, % |
1000 |
2000 |
3000 |
5000 |
10000 |
|
5 |
0 |
0.8603 |
0.8616 |
0.8644 |
0.8662 |
0.8666 |
|
5 |
0.7077 |
0.6949 |
0.7025 |
0.6982 |
0.7089 |
|
|
10 |
0.6415 |
0.6743 |
0.6839 |
0.6862 |
0.6825 |
|
|
15 |
0.5796 |
0.6042 |
0.5861 |
0.5941 |
0.5961 |
|
|
20 |
0.5755 |
0.5357 |
0.5515 |
0.5546 |
0.5465 |
|
|
10 |
0 |
0.9967 |
1 |
1 |
1 |
1 |
|
5 |
0.9314 |
0.9361 |
0.9414 |
0.9419 |
0.9482 |
|
|
10 |
0.7076 |
0.7165 |
0.7158 |
0.7093 |
0.7248 |
|
|
15 |
0.6241 |
0.6086 |
0.6315 |
0.6351 |
0.6355 |
|
|
20 |
0.5711 |
0.5873 |
0.5778 |
0.5946 |
0.5753 |
|
|
15 |
0 |
0.9981 |
1 |
1 |
1 |
1 |
|
5 |
0.9916 |
0.9994 |
0.9997 |
0.9998 |
0.9999 |
|
|
10 |
0.9271 |
0.9607 |
0.9785 |
0.9863 |
0.9924 |
|
|
15 |
0.7314 |
0.7904 |
0.7769 |
0.7919 |
0.7991 |
|
|
20 |
0.6372 |
0.6155 |
0.6255 |
0.6358 |
0.6603 |
|
|
20 |
0 |
0.9982 |
1 |
1 |
1 |
1 |
|
5 |
0.9949 |
0.9994 |
0.9997 |
0.9998 |
0.9999 |
|
|
10 |
0.9864 |
0.9978 |
0.9987 |
0.9993 |
0.9996 |
|
|
15 |
0.9095 |
0.9524 |
0.9469 |
0.9653 |
0.9809 |
|
|
20 |
0.7415 |
0.7679 |
0.7678 |
0.7825 |
0.7834 |
|
|
30 |
0 |
0.9992 |
1 |
1 |
1 |
1 |
|
5 |
0.997 |
0.9998 |
0.9999 |
0.9999 |
1 |
|
|
10 |
0.9931 |
0.9993 |
0.9995 |
0.9997 |
0.9999 |
|
|
15 |
0.9862 |
0.9979 |
0.9985 |
0.9993 |
0.9997 |
|
|
20 |
0.9386 |
0.9729 |
0.9907 |
0.9975 |
0.9988 |
Параметры кода были выбраны в соответствии с рекомендациями, приведенными в работе [5].
По результатам моделирования приведем основные выводы:
Код неэффективен при доле избыточных пакетов меньше 5 %. Это обусловлено, прежде всего, особенностью конструкции кода: при малом количестве кодовых символов не все исходные сообщения могут быть включены в процесс кодирования (так как процесс включения является случайным).
Для устойчивого декодирования на приемном конце с учетом стирания в канале достаточно иметь избыточность пакетов порядка пяти процентов.
Результаты исследования показывают перспективность дальнейших исследований класса стирающих кодов для последующего их применения в системах с коммутацией пакетов.
- Литература:
Luby M. LT Codes // Proc. of the 43rd Annual IEEE Symp. on Foundations of Computer Science (FOCS). – 2002. – P. 271–282.
Варгаузин В. Помехоустойчивое кодирование в пакетных сетях // ТелеМультиМедиа. – 2005. – №3. – C.10–16.
Simon S. Woo, Michael K. Cheng Prioritized LT Codes // Conference of Information Science and Systems, Princeton, New Jersey, March 19, 2008. – P. 1-6.
К.В. Шинкаренко, А.М. Кориков Исследование эффективности помехоустойчивых кодов Лаби // Доклады ТУСУРа. 2009. №1 часть 1. С. 185-192.
D.J.C. MacKay Fountain codes // IEEE Proc.-Commun., Vol. 152, No. 6, December 2005. – P. 1062-1068.