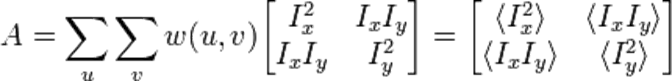Методы поиска угловых особенностей на изображениях

В статье рассматриваются существующие и наиболее популярные методы поиска углов на изображениях.

Детектор углов или в более общей терминологии детектор точечных особенностей является подходом, применяемым в системах компьютерного зрения для извлечения определенных особенностей изображения. Детектор углов часто используется в методах обнаружения движения, сравнения изображений, слежения, совмещении панорамных снимков, 3х мерном моделировании и распознавании объектов. Формализация

Угол может быть определен как пересечение двух ребер. Угол может быть также определен в качестве отправной точки, для которой есть два доминирующих и различных направления в края в окрестности точки.

Точечная особенность является точкой на изображении, которая имеет четко определенные позиции и может быть надежно обнаружена. Это означает, что особая точка может быть угловой, но она также может быть, например, изолированной точкой локального максимума линии интенсивности или минимумом, концом линии или точкой на кривой, где кривизна локально максимальна.

На практике большинство детекторов углов обнаруживают точечные особенности, а не углы. Вследствие этого, если только углы должны быть обнаружены необходимо сделать локальный анализ обнаруженных точечных особенностей и определить какие из них действительно углы.

В литературе "угол", "точечная особенность" и "особенность" используются как синонимы, которые не добавляют ясности. В частности, есть несколько детекторов пятен, которые могут быть представлены как "точки интереса операторов", но которые иногда ошибочно называют "детекторами углов". Кроме того, существует понятие обнаружения хребта для обнаружения удлиненных объектов.

Детекторы углов обычно не очень надежны и часто требуют контроля эксперта или больших упрощений в целях предотвращения влияния отдельных ошибок со стороны доминирующих задач распознавания.

О качестве детектора углов часто судят по его способности обнаруживать тот же угол в нескольких изображениях, которые являются аналогичными, но не идентичными, например, с различным освещением, перемещением, вращением и другими преобразованиями.

Простым способом обнаружения углов является применение корреляции, но этот метод вычислительно дорог и неоптимален. Альтернативный подход часто основан на методе, предложенного Харрисом и Стивенсом, который, в свою очередь, является усовершенствованием метода Моравека. Алгоритм обнаружения углов Моравека

Это один из первых алгоритмов обнаружения углов и определяет угол, чтобы тот был в точке с низкой автомодельностью. Алгоритм проверяет каждый пиксель в изображении, чтобы определить является ли тот углом, рассматривая участки в области пикселя. Сходство определяется путем принятия суммы квадратов разностей между двумя участками. Меньшее число указывает на большее сходство.

Если пиксель в области равномерной интенсивностью, то близлежащие участки будут выглядеть примерно одинаково. Если пиксель находится на краю, тогда соседние участки в направлении, перпендикулярном к краю будет выглядеть совершенно разными, но соседние участки в направлении, параллельном краю изменяются незначительно. Если пиксель на особенности с изменением во всех направлениях, то ни один из близлежащих участков не будет выглядеть примерно также.

Сила угла определяется как наименьшая сумма квадратов разностей между участком и его соседями (по горизонтали, вертикали и двум диагоналям). Если это число локально максимально, то особенность присутствует.

Как отметил Моравек, одна из главных проблем этого метода связана с тем, что он не изотропен: если угол не направлен в сторону соседей, то он не будет обнаружен, как точечная особенность. Детектор Харриса

Харрис и Стивенс улучшили детектор углов Моравека, рассматривая дифференциальную оценку угла по отношению к направлению непосредственно, вместо использования сдвинутых пятен. Эту оценку угла часто называют автокорреляционной, поскольку этот термин используется в том документе, в котором этот детектор описан. Однако с математической точки зрения используется метод суммы квадратов разностей.

Без потери общности будем считать, что используются полутоновые 2-мерные изображения. Пусть это изображение будет задано I. Рассмотрим вопрос о выделении области изображения (U, V) и перехода его по (х, у). Взвешенную сумму квадратов разностей между этими двумя областями, обозначим S, определяющуюся по формуле:

I (u + x , v + y) может быть аппроксимирована рядом Тейлора. Пусть I_x и I_y - будут частными производными от I, такими, что

Это приводит к приближению

которое можно записать в матричном виде:

где А - структура тензора,

Эта матрица - матрица Харриса, а угловые скобки означают усреднение (например, суммирование (U, V)). Если используется круглое окно (или округлые взвешенные окна, такие, как гауссовские), то ответ будет изотропным.

Угол (или, в общем, точечная особенность) характеризуется большим изменением S во всех направлениях вектора . На основе анализа собственных значений A, эта характеристика может быть выражена следующим образом: должно быть два "больших" собственных значения для точечных особенностей. На основании величины собственных значений, можно сделать следующие выводы на основе этих аргументов:

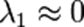1. Если и 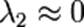то этот пиксель (х, у) не имеет особенности, представляющей интерес.

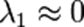2. Если и λ 2 имеет некоторое большое положительное значение, то обнаружен край.

3. Если λ 1 и λ 2 большие положительные значения, то угол найден.

Харрис и Стивенс отметили, что точное определение собственных значений вычислительно дорого, так как требует вычисления квадратного корня, а вместо этого предложить следующие функции с M, где κ является настраиваемым параметром чувствительности:

Таким образом, алгоритм не имеет на самом деле вычисления собственного разложения матрицы, а вместо этого достаточно вычислить определитель и след от A найти углы, или, вернее, точки интереса в целом.

Значение κ должно быть определено эмпирически, так и в литературе были представлены как возможные значения в диапазоне 0,04 - 0,15.

Ковариационная матрица для позиции угла A^-1, т. е. 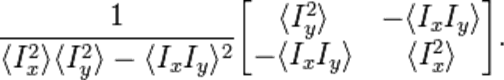Масштабируемый оператор Харриса

Вычисление матрицы второго момента A(иногда также называют структурой тензора) в операторе Харриса, требует вычисления производных изображения I x , I y в области изображения, а также суммы нелинейных комбинаций этих производных по соседству. Так как вычисление производных обычно включает этап расширения сглаживания пространства, оперативное определение оператора Харриса требует два параметра масштабирования: (i) в местном масштабе для сглаживания до вычисления производных изображения и (ii) степени интеграции накопления нелинейных операций по производным операторов в единый дескриптор изображения.

Если I обозначает интенсивность оригинального изображения, пусть L обозначает масштаб пространства представление I полученное путем свертки с гауссовым ядром

с локальным параметром масштабирования t:

и пусть и обозначают частные производные от L. Кроме того, введем гауссовскую весовую функцию g (x , y , s) с интеграционным параметром масштабирования s. Тогда масштабируемая матрица второго момента может быть определена как

Теперь мы можем вычислить собственные значения μ таким же образом, как и для A, и определить масштабируемую меру углов Харриса

. .

Что касается выбора местного параметра масштаба t и масштаба параметров интеграции S, эти параметры масштаба, как правило, связанных между собой относительный показатель степень интеграции γ таким, что s = γ 2 t, где γ обычно выбирается в интервале . Таким образом, мы можем вычислить масштабируемую меру углов Харриса M_c (x , y; t ,γ 2 t) в любом масштабе t в расширении пространства для получения многомасштабных детекторов углов, который реагирует на структуру углов разного размера в области изображения.

На практике этот масштабируемый детектор углов часто дополняется шагом выбора масштабирования, где масштаб-нормированный оператор Лапласа (Линдеберга 1998)

рассчитывается в каждом масштабе в масштабах пространства и масштаба адаптированы угловых точек с автоматическим выбором масштаба ("Харрис-Лапласа") вычисляются по точкам, которые являются одновременно:

• пространственных максимумов многомасштабных мер углов M c (x , y; t ,γ 2 t)

• локальных максимумов и минимумов в масштабах шкалы-нормированные оператор Лапласа

.

Алгоритм поиска углов Ши-Томаси

Обратите внимание, что его также иногда называют детектором углов Канаде-Томаси.

Детектор углов во многом основан на угловом детекторе Харриса. Авторы показывают, что для областей изображения проходят аффинные преобразования, min(λ1,λ2) является более точным измерением силы угла, чем Mc. Подход определения кривизны кривой

Ранние подходы в обнаружении углов обнаруживали места, где кривизна линий и градиент одновременно высоки. Дифференциальный способ выявления таких точек для вычисления кривизны масштабированной кривой (произведение кривизны и градиента в степени 3)

и выявлять положительные максимумы и отрицательные минимумы этого дифференциального выражения в некотором масштабе t в масштабах пространства L представление исходного изображения. Основной проблемой этого подхода, является то, что он очень чувствителен к шуму и к выбору масштабного уровня. Лучший метод для расчета γ-нормированной масштабированной кривизны

с γ = 7 / 8, а также обнаружения подписали расширения пространства максимумов этого выражения, которые являются центрами и масштабах, которые максимумов положительных и отрицательных минимумов по отношению к пространства и масштаба

в сочетании с дополнительным шагом локализации справиться с увеличением локализации ошибки на грубые весы. Таким образом, большие значения масштаба будут связаны с закругленными углами большой пространственной протяженности, в то время как меньшие значения масштаба будут связаны с острыми углами с небольшой пространственной протяженности. Такой подход является первым детектором углов с автоматическим выбором масштаба (до "Харрис-Лапласа" выше), и был использован для отслеживания углов под большие изменения масштаба в области изображения.

Детектор углов Тайковича и Хедли

Этот детектор непосредственно проверяет область около пикселя путем изучения близлежащих пикселей. является пикселем, подлежащим рассмотрению, а является точкой на окружности P вокруг . Точка является точкой противоположной по диаметру.

Функции отклика определяется как:

Эта величина будет большой, когда нет направления, в котором центральный пиксель похож на два близлежащих пикселя по диаметру. Р - это дискретизированный круг ( круг Брезенгема ), поэтому используется интерполяции для промежуточных диаметров чтобы дать более изотропной ответ. Так как любой расчет дает верхнюю границу min, горизонтальное и вертикальное направления проверяются в первую очередь для определения имеет ли смысл переходить к полному вычислению с. FAST детектор особенностей

FAST является аббревиатурой для "Особенности ускоренных испытаний сегмента".

Детектор считает пиксели в круге Брезенгема радиуса r вокруг точки кандидата. Если n смежных пикселей ярче чем центр, по крайней мере, в t раз или темнее центра то пиксель под центром считается особенностью. Хотя r в принципе, может принимать любое значение, только значение 3 используется (соответствующий круг 16 пикселей окружности), и тесты показывают, что оптимальное значение n 9. Это значение n наименьшее, при котором края не обнаруживаются. Результирующий детектор производит очень стабильные особенности. Кроме того, ID3 алгоритм используется для оптимизации порядка, в котором испытываются пиксели, в результате чего получается наиболее вычислительно эффективный детектор особенностей. Литература:

1. C. Harris and M. Stephens. "A combined corner and edge detector"// Proceedings of the 4th Alvey Vision Conference. – 1988. - P. 147–151.

2. C. Tomasi and T. Kanade. "Detection and Tracking of Point Features"// Pattern Recognition. – 2004 . – P. 12-15.

3. T. Tommasini. Making good features to track better / T. Tommasini, A. Fusiello, E. Trucco, and V. Roberto // Proceedings IEEE Computer Society Conference on Computer Vision Pattern Recognition. - 1998. - P. 145-149.

4. M. Trajkovic and M. Hedley. "Fast corner detection"// Image and Vision Computing 16 (2). – 1998. – P. 75–87.

5. H. Wang and M. Brady. "Real-time corner detection algorithm for motion estimation"// Image and Vision Computing 13 (9). - 1995. – P. 695–703.