Как известно, метод последовательной смены стационарных состояний (ПССС) основан на следующих предпосылках: в каждый момент времени существует конечная возмущенная область, в которой происходит движение газа к скважине; движение внутри возмущенной области стационарно; размер возмущенной области определяется из уравнения материального баланса [1,2]. В данной статье предложено решение задачи о притоке газа к скважине методом последовательной смены стационарных состояний с учетом влияния начального градиента.
Ключевые слова: газ, возмущенная область, начальный градиент, радиус, давление.
As is known, the method of sequential change of stationary states (SCSS) is based on the following assumptions: at each time there is a finite perturbed area in which the gas moves to the well; the movement within the perturbed area is stationary; the size of the perturbed area is determined from the material balance equation [1,2]. This article proposes a solution to the problem of gas inflow to the well by the method of sequential change of stationary states, taking into account the influence of the initial gradient.
Keywords: gas, perturbed area, initial gradient, radius, pressure.
Дифференциальное уравнение движения газа с учетом влияния начального градиента имеет следующий вид:
(1)
или
(2)
Используя формулу для плотности 
м (2) и провода некоторые преобразования, получаем:
(3)
или
Интегрируя, получаем его общее решение в виде:
(4)
Постоянные интегрирования 
и 
находятся из граничных условий, которые в данном случае можно записать в виде:
при 
,
при 
.
Представляя граничные условия в общее решение (4) находим:
,
,
откуда
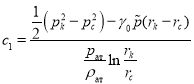(5)
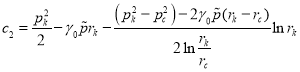(6)
Подставляя (5) и (6) в (4) получаем закон распределения давления в плоскорадиальном потоке:
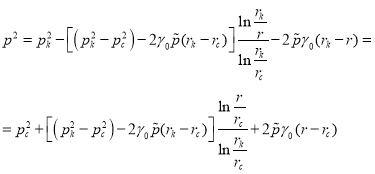(7)
Градиент давления и скорость фильтрации определяем, взяв производную правой и левой части (7):
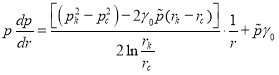(8)
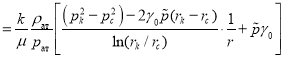(9)
Тогда для дебита получается следующая формула:
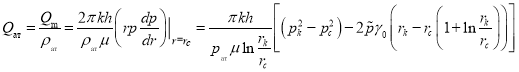(10)
Для решения поставленной задачи сначала определим средневзвешенное по объему порового пространства пластовое давление в плоскорадиальном потоке газа. Оно определяется по формуле
(11)
в нашем случае 
,
(12)
а давление определяется по формуле (7). Так как в первой фазе радиус контура возмущенной области зависит от времени, то пусть в полученных формулах 
. Тогда учитывая формулы (7) и (12) в (11) получаем:
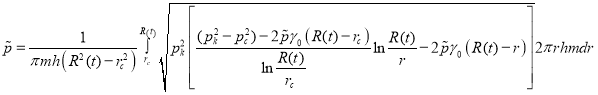
(13)
Здесь 
имеется как в правой, так и в левой части выражения под знаком интеграла. Чтобы получить выражение для 
в правой части вместо подставим 
. Тогда получаем из (13) следующее выражение:
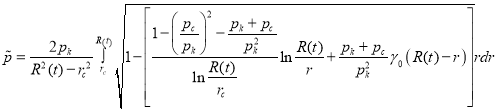(14)
Делая подстановку
,
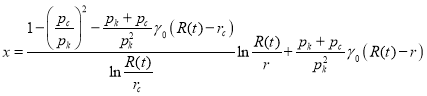где
и удержав два первых члена ряда 
получаем:
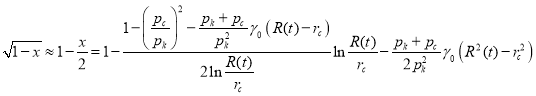(15)
Далее, учитывая (15) и принимая метод, интегрируя по частям для выражение (14), подставляя пределы интегрирования, произведя преобразование и пренебрегая членами 
получаем для 
следующее выражение:
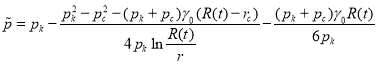(16)
Так как отбор газа происходит с постоянным дебитом 
, отобранная масса газа к моменту t равна 
.
Начальный запас газа (при 
) в зоне пласта радиусом 
равен
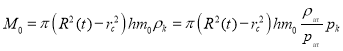(17)
Текущий запас газа выразим через средневзвешенное давление 
:
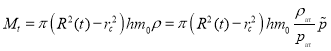(18)
Таким образом, 
(19)
Подставляя в (19) формулы (10), (16), (17), (18), получаем
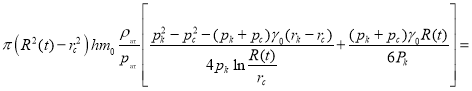
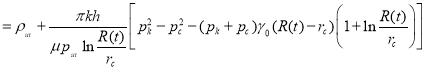
или
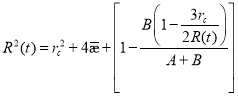(20)
где 
, 
,
,
(21)
Здесь 
находится методом установившихся отваров. Как видим, при 
мы получаем закон движения границы возмущенной области 
без учета влияния начального градиента,
(22)
При появлении начального градиента 
, радиус границы возмущения 
уменьшается. Это можно установить сравнением правых частей формул (20) и (22).
Таким образом, в данной статье получены приближенные формулы для определения размера области возмущения при фильтрации газа с учетом влиянии начального градиента.
Литература:
- Подземная гидравлика. Учебник для вузов./ Л. С. Басниев, А. М. Власов, И. Н. Кочина, В. М.Максимов. — М.:Недра, 1986.303 с.
- Чарный И. А. Подземная гидродинамика. М.: Гостоптехиздат, 1963.
