Как известно, одним из наиболее простых приближенных методов решения задач является метод последовательной смены стационарных состоянии (ПССС), который широко применяется в практических расчетах [1].
Метод основан на предположении, что в каждый момент времени вся область движения жидкости, которая охватывает весь пласт, условно разделяется на две области, возмущенную и невозмущенную. При этом предполагается, что в возмущенной области, начинающейся от стенки скважины, давление распределяется так, как будто бы движение жидкости в ней — установившееся, и внешняя граница этой области служит в данный момент контуром питания. В невозмущенной области пласта давление всюду постоянно и равно начальному статическому. Закон движения подвижной границы раздела возмущенной и невозмущенной областей определяется при помощи уравнения материального баланса и граничных условий.
Разделение фильтрационного потока на две области вызывает необходимость рассматривать процесс перераспределения пластового давления, протекающего в две фазы. В течение первой фазы радиус возмущенной области непрерывно растет. И в тот момент, когда она достигнет естественной границы пласта, начинается вторая фаза.
Ключевые слова: неустановившийся, приближенный, начальный градиент, фаза, плоскорадиальный.
As is known, one of the simplest approximate methods for solving problems is the method of sequential change of stationary states (SCSS), which is widely used in practical calculations [1].
The method is based on the assumption that at any given time the entire fluid flow region, which covers the entire formation, is conditionally divided into two regions, perturbed and undisturbed. It is assumed that in the perturbed region, starting from the wall of the well, the pressure is distributed as if the movement of the liquid in it is steady, and the outer boundary of this region serves at the moment as a supply circuit. In the undisturbed region of the formation, the pressure is everywhere constant and equal to the initial static. The law of motion of the movable boundary of the perturbed and undisturbed areas is determined by the equation of material balance and boundary conditions.
The separation of the filtration flow into two regions makes it necessary to consider the process of redistribution of reservoir pressure flowing in two phases. During the first phase, the radius of the perturbed region continuously increases. In the moment it reaches the natural boundary of the formation, the second phase begins.
Keywords: unsteady, approximate, initial gradient, phase, plane-radial.
Рассмотрим теперь расчет плоскорадиальных неустановившихся фильтрационных потоков жидкости с помощью метода ПССС, с учетом влияния начального градиента.
Как известно, дифференциальное уравнение движения жидкости с учетом влияния начального градиента имеет вид:
(1)
Решим это уравнение, используя граничные условия:
при 
;
при 
. (2)
Находим последовательно
или 
,
, откуда 
(3)
Постоянные интегрирования 
и 
находятся из граничных условий (2).
Подставляя граничные условия в общее решение (3), находим
откуда
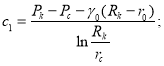(4)
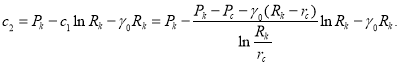(5)
Подставляя (4) и (5) в общее уравнение (3), получим закон распределения в плоскорадиальном потоке:
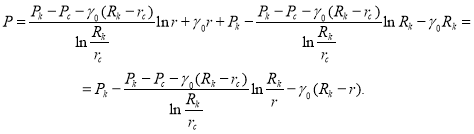(6)
Сначала определим средневзвешенное по объему порового пространства пластовое давление в плоскорадиальном потоке жидкости. Она определяется по формуле
(7)
в нашем случае 
, 
, (8)
а давление определяется по формуле (6).
Подставив эти выражения в (7) и используя метод интегрирования по частям, получим
.
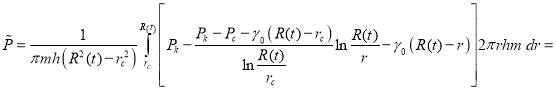
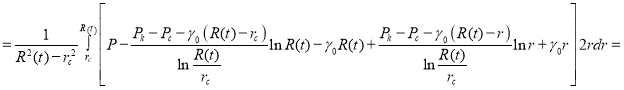
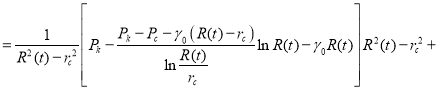
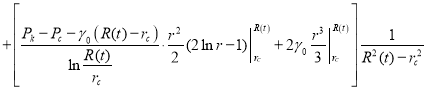Произведя преобразования и пренебрегая членами с 
получаем следующее выражение:
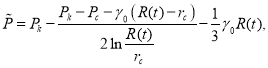(9)
откуда
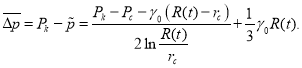(10)
С другой стороны, учитывая, что количество продукции 
, добытой за время 
, равно изменению упругого запаса жидкости в возмущенной зоне пласта за тот же промежуток времени, то можно написать:
(11)
где 
– коэффициент упругоемкости пласта. Для определения используем формулу распределения давления (9).
Так как
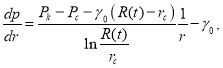
то
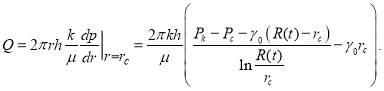(12)
Учитывая в формуле (11) формулы (10), (12) и формулу 
мы получаем:
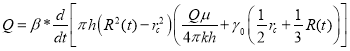(13)
или
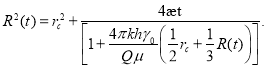(14)
Здесь 
.
При 
мы получаем закон давления границы возмущенной области 
без учета влияния начального градиента:
(15)
что полностью совпадает с известной формулой [1,2].
Уравнение (14) является кубическим уравнением относительно :
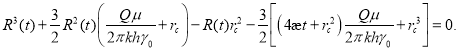(16)
Однако, если учесть, что 
то, уравнение (14) можно представить в виде:
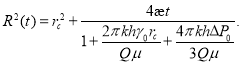(17)
Здесь 
можно найти с помощью исследованных скважин методом установившихся отборов.
Таким образом, в статье найден закон движения границы возмущенной области 
для плоскорадиальной неустановившейся фильтрации упругой жидкости при наличии влияния начального градиента.
Литература:
- Подземная гидравлика. Учебник для вузов/К. С. Басниев, А. М. Власов, И. Н. Кочина, В. М. Максимов. — М.: Недра, 1986. — 303 с.
- Чарный И. А. Подземная гидрогазодинамика. М.: Гостоптехиздат, 1963.
