Численное изучение напряжений и перемещений в арке из гофрированного U-образного тонкостенного профиля системы MIC-120 при загружении гравитационной нагрузкой для определения критической нагрузкой.
Ключевые слова: вальцованный U-образный профиль системы MIC-120, напряжения в арках, ветровая нагрузка, гидростатическое давление, критическая нагрузка в арках из вальцованных конструкций, компьютерное моделирование.
Numerical study of stresses and displacements in a corrugated U-shaped thin-walled arch of the MIC-120 system under gravitational load to determine the critical load.
Keywords: rolled U-shaped profile of MIC-120 system, stresses in arches, wind load, hydrostatic pressure, critical load in arches of rolled structures, computer modeling.
Сравнив напряжения и перемещения в арках из гофрированного U образного с гладким Т образного сечений и учитывая численно жесткостные характеристики рекомендованными техническими условиями ТУ 5283–147–02494680–2004 определили необходимость учета коэффициента условий работы вальцованной конструкции [4]. Получив нормальные напряжения, превышающие предельные при загружении критической нагрузкой, определим величину предельной нагрузки, при которой перемещения и нормальные напряжения не будут превышать предельных значений [2].
Материалы и методы: По твердотельной модели, выполненной в программном комплексе Solid Works в виде одного арочного вальцованного профиля U образного сечения пролетом 18 м, загрузим распределенной нагрузкой для сравнения напряженного состояния и величины перемещений в арке [1]. Формы поперечных сечений показаны на рисунке 1 статьи [1]. Арочные профили были рассчитаны методом конечных элементов и выявлены изменения напряжений и перемещений при изменении гравитационной нагрузки.
Для определения максимально допустимой вертикальной равномерно распределенной нагрузки арочного профиля использовали модель пролетом 18 м в виде двухшарнирной статически неопределимой арки. Закрепляем связями верхние грани профилей из плоскости изгиба, учитывая, что в реальных конструкциях сводов соседние стенки профилей сцеплены и сдерживают друг друга. Загрузим арку гравитационной нагрузкой, и постепенно будем увеличивать до получения предельного перемещения и напряжения. В твердотельной модели загружение приложено к гофрированной нижней полке профиля, нормально граням.
Результаты вычислений по нормальным напряжениям отражены на рис. 2. На рис. 2 показано начало превышения предельного напряжения Ry =343232750Н/м2 и 3,57е+8Н/м2 происходящем уже при 0,0002175Н/мм2. Таким образом при нагрузке выше 0,0002175Н/мм2 в конструкции надо учитывать усталость.
Сравним результаты расчетов по предельным перемещениям, изменения перемещений в зависимости от изменения нагрузки отражены на рис. 1. Предельные перемещения наступают при 0,0001144Н/мм2 (перемещения 72 мм).
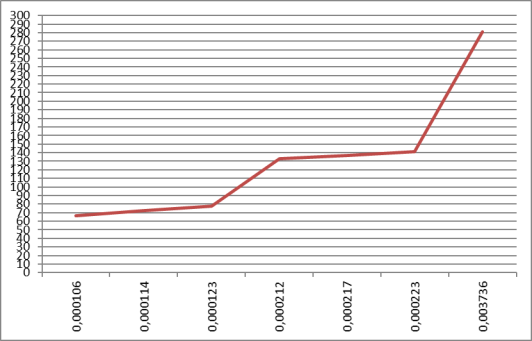
Рис. 1.Изменения перемещений от равномерно распределенной нагрузки в гофрированном арочном профиле полученных твердотельным моделированием пролетом 18 м t=0,8 мм (при гравитационной нагрузке)
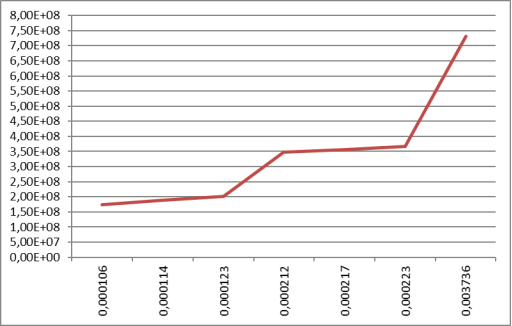
Рис. 2.Изменения напряжений от равномерно распределенной нагрузки в гофрированном арочном профиле полученных твердотельным моделированием пролетом 18 м t=0,8 мм (при гравитационной нагрузке)
Данные расчета актуальны при действии гравитационной нагрузки при закреплении стенок профилей конструкции из плоскости. При отсутствии диафрагм жесткости жесткость в плоскости работы уменьшается и напряжения меняются. Влияние воздействия закрепления из плоскости или жесткости из плоскости свода было показано ранее при сравнении перемещений и форм деформаций экспериментальных данных с численным расчетом [3].
Результаты: просчитали величины предельных значений равномерно распределенной нагрузки для вальцованных тонкостенных конструкций при условии закрепления верхних граней из плоскости и отразили в таблице № 1 (интерполяцию не использовать).
Таблица 1
|
Толщина профиля, мм |
Напряжения МАХ,Н/м2 |
Напряжения МIN, Н/м2 |
Величина нагрузки, Н/мм2 |
Перемещения, мм |
|
0.6 |
0.0000733 |
72.0 |
||
|
0.6 |
3.43E+08 |
-3.04E+08 |
0.0001655 |
|
|
0.6 |
3.57E+08 |
-3.13E+08 |
0.0001713 |
|
|
0.7 |
0.0000946 |
72.0 |
||
|
0.7 |
3.43E+08 |
-2.85E+08 |
0.0001925 |
|
|
0.7 |
3.57E+08 |
-3.00E+08 |
0.0002017 |
|
|
0.8 |
0.0001144 |
72.0 |
||
|
0.8 |
3.43E+08 |
-2.93E+08 |
0.0002098 |
|
|
0.8 |
3.57E+08 |
-3.05E+08 |
0.0002175 |
|
|
0.9 |
0.0001360 |
72.0 |
||
|
0.9 |
3.43E+08 |
-2.66E+08 |
0.0002697 |
|
|
0.9 |
3.57E+08 |
-2.92E+08 |
0.0002488 |
|
|
1 |
0.0001592 |
72.0 |
||
|
1 |
3.43E+08 |
-2.66E+08 |
0.0002699 |
|
|
1 |
3.57E+08 |
-2.78E+08 |
0.0002809 |
|
|
1.1 |
0.0001825 |
72.0 |
||
|
1.1 |
3.43E+08 |
-2.80E+08 |
0.0003294 |
|
|
1.1 |
3.57E+08 |
-2.92E+08 |
0.0003427 |
|
|
1.2 |
0.0002076 |
72.0 |
||
|
1.2 |
3.43E+08 |
-2.67E+08 |
0.0003645 |
|
|
1.2 |
3.57E+08 |
-2.78E+08 |
0.0003789 |
Выводы: получены максимально возможные предельные величины вертикальных равномерно распределенных нагрузок при наступлении предельных нормальных напряжений и перемещений.
Литература:
- Веселев Ю. А., Карабутов М. С. Приведение вальцованного U-образного профиля с редуцированными жесткостными характеристиками к гладкому тавровому профилю. // Строительная механика инженерных конструкций и сооружений. -2012 год. № 1, -С.30–37.
- Веселев Ю. А., Карабутов М. С. К вопросу о надежности тонкостенных металлических сводов из вальцованных профилей//«Строительство-2013» «Современные проблемы промышленного и гражданского строительства» «материалы международной научно-практической конференции». -Ростов н/Д: Рост. гос. строит. ун-т, 2013. -43с.
- М. С. Карабутов Сравнение поведения твердотельно смоделированной арки из вальцованного U-образного профиля с результатами экспериментальных данных при действии ветрового давления.// Молодой ученый.-2019.№ 40. -С.16–19.
- М. С. Карабутов Численное сравнение напряженно деформированных состояний арки из вальцованного U-образного профиля и арки с приведенным Т-образным сечением полученным по редуцированным жесткостным характеристикам определенным твердотельным моделированием. // Молодой ученый.-2019.№ 41. -С.14–17.







