Как известно, метод А. М. Пирвердяна аналогичен методу последовательной смены стационарных состояний (ПССС) и уточняет его [1]. В этом методе, как и в методе ПССС неустановившийся фильтрационный поток в каждый момент времени мысленно разбивается на две области — возмущенную и невозмущенную. Граница между этими областями также определяется из уравнения материального баланса. Но в отличие от метода ПССС распределение давления в возмущенной области по методу А. М. Пирвердяна задается в виде квадратичной параболы так, чтобы пьезометрическая кривая на границе областей касалась горизонтальной линии, представляющей давление в невозмущенной области. Автор данной статьи предлагает то, что в возмущенной области степень параболы был не квадратичный, а произвольный действительный. В работе также учитывается влияние начального градиента.
Ключевые слова: неустановившийся, прямолинейно-параллельный, возмущенная область, парабола, начальный градиент.
As is known, the method of A. M. Pirverdyan the same method of sequential change of stationary states (SCSS) and clarifies it [1]. In this method, as in the method of SCSS unsteady filtration flow at each time mentally divided into two areas — perturbed and undisturbed. The boundary between these areas is also determined from the material balance equation. But unlike the SCSS pressure distribution in the perturbed region by the method of A. M. Pirverdyan is set in the form of quadratic parabola so that the piezometric curve in the border areas concerned the horizontal lines representing the pressure in the unperturbed region. The author of this article suggests that in the perturbed region the degree of the parabola was not quadratic but arbitrary real. The paper also takes into account the influence of the initial gradient.
Keywords: unsteady, rectilinear-parallel, perturbed area, parabola, initial gradient.
Рассмотрим прямолинейно-параллельный неустановившийся фильтрационный поток упругой жидкости. Предположим, в горизонтальном пласте постоянной толщины h и ширины В пущена в эксплуатацию галерея с постоянным дебитом Q. К моменту времени t после пуска границы возмущенной области продвинутся на длину l(t), при этом кривая распределения давления в этой области будет иметь вид параболы степени ![]() , где
, где ![]() Уравнение пьезометрической кривой в возмущенной области задается в виде:
Уравнение пьезометрической кривой в возмущенной области задается в виде:
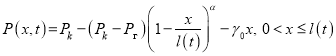 , (1)
, (1)
где ![]() — начальный градиент.
— начальный градиент.
Дебит галереи определяется по закону Дарси:
Значение градиента давления на галерее ![]() найдём по формуле (1)
найдём по формуле (1)
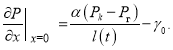 (3)
(3)
Подставив равенство (3) в (2), находим формулу для дебита галереи:
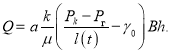 (4)
(4)
Закон движения внешней границы возмущенной области определяется из уравнение материального баланса:
![]() (5)
(5)
где объем возмущенной области пласта:
![]() (6)
(6)
![]() , (7)
, (7)
где ![]() – средневзвешенное пластовое давление.
– средневзвешенное пластовое давление.
Определим значение средневзвешенного пластового давления в возмущенной области к моменту времени t, используя распределение давления (1):
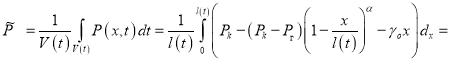
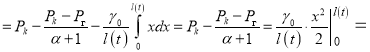
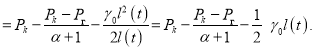 (8)
(8)
Тогда с учетом (4) находим:
![]() . (9)
. (9)
Из уравнения (4) находим:
![]() (10)
(10)
Учитывая (10) в (9), получаем:
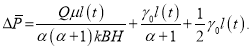 (11)
(11)
Подставляя (6), (9) и (11) в уравнение материального баланса (5), получаем:
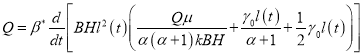 (12)
(12)
или
![]() (13)
(13)
При ![]() для размера области возмущения получаем известную формулу
для размера области возмущения получаем известную формулу
![]() (14)
(14)
а в общем случае получается кубическое уравнение:
![]()
или 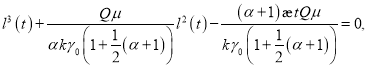 (15)
(15)
решая которое, можно найти ![]() .
.
Уравнение (13) можно преобразовать в следующий вид:
![]()
или
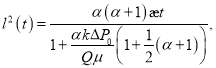 (16)
(16)
где ![]()
Следует отметить, что можно подобрать такое значение ![]() , при котором формулы наиболее будут близки к точным решениям.
, при котором формулы наиболее будут близки к точным решениям.
Таким образом, в данной статье получены приближенные формулы для определения размера области возмущения, а также формулы для распределения давления в возмущенной области. Для этого достаточно использовать формулы (1) и (16).
Литература:
- Подземная гидравлика. Учебник для вузов/К. С. Басниев, А. М. Власов, И. Н. Кочина, В. М. Максимов. — М.: Недра, 1986. — 303 с.
- Чарный И. А. Подземная гидрогазодинамика. М.: Гостоптехиздат, 1963.







