Метод «усреднения» Г. П. Гусейнова заключается в том, что в дифференциальном уравнении упругого режима производная от давления по времени ![]() усредняется по всей возмущенной области и заменяется некоторой функцией времени,
усредняется по всей возмущенной области и заменяется некоторой функцией времени, ![]() значение которой определяется из начальных и граничных условий [1,2,3].
значение которой определяется из начальных и граничных условий [1,2,3].
В статье предлагаются формулы, по которым можно более простыми способами решать гидродинамические задачи, связанные с неустановившейся фильтрацией упругой жидкости в пористой среде с учетом влияния начального градиента давления.
Ключевые слова: плоскорадиальный, неустановившийся, начальный градиент, метод усреднения, упругая жидкость.
The method of «averaging» of G. P. Huseynov is that in the differential equation of the elastic regime, the pressure derivative is averaged over the entire perturbed area and replaced by a certain time function, the value of which is determined from the initial and boundary conditions [1,2,3].
The paper proposes formulas that can be used in simpler ways to solve hydrodynamic problems associated with unsteady filtration of an elastic liquid in a porous medium, taking into account the influence of the initial pressure gradient.
Keywords: plane-radial, unsteady, initial gradient, averaging method, elastic fluid.
Предположим, что дифференциальное уравнение упругого режима для плоскорадиального течения жидкости с учетом влияния начального градиента имеет следующий вид:
![]() (1)
(1)
Уравнение (1) решается при следующих условиях:
Условие на забое имеет вид:
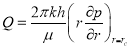 (2)
(2)
На границе возмущенной области имеем:
![]() при
при ![]() (3)
(3)
![]() при
при ![]() (4)
(4)
Где второе условие представляем собой как условие гладкости кривой
Интегрируя (1) получим:
![]() (5)
(5)
Для определения ![]() используем условие (4):
используем условие (4):
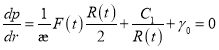
или
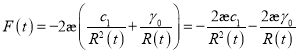 (6)
(6)
С другой стороны из (2) имеем,
![]()
с учетом (6) получаем:
или 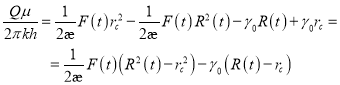 (7)
(7)
Из последнего выражения после несложных преобразований получаем:
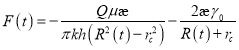 (8)
(8)
Для получения распределения давления используем формулу (5):
![]() (9)
(9)
При ![]() получаем:
получаем:
![]() (10)
(10)
Вычитая из (10) выражение (9) получаем:
![]() (11)
(11)
Если вместо ![]() подставить выражение полученное из (6), т. е.
подставить выражение полученное из (6), т. е. ![]() то получим выражение для распределение давления в виде:
то получим выражение для распределение давления в виде:
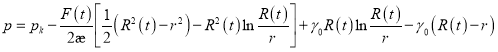 (12)
(12)
Если в (12) вместо ![]() подставить выражение (8) то получим следующее выражение:
подставить выражение (8) то получим следующее выражение:
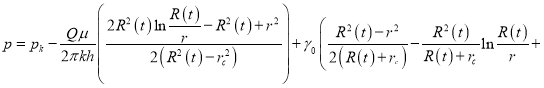
![]() (13)
(13)
Если в (13) пренебречь значениями ![]() в связи их малостью и продифференцируем по
в связи их малостью и продифференцируем по ![]() , то получим:
, то получим:
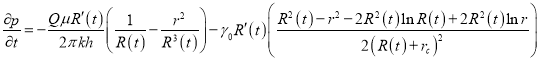 +
+
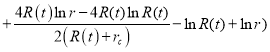 (14)
(14)
Учитывая выражения (8) и (14) в формуле
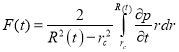 (15)
(15)
получаем:
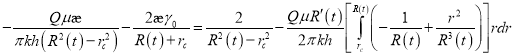
![]() (16)
(16)
или
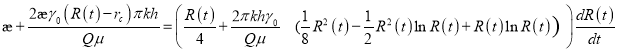 (17)
(17)
Если интегрировать правую и левую части (17) методом интегрирования по частям и после пренебречь выражениями ![]() в связи их малостью получим выражение:
в связи их малостью получим выражение:
![]()
![]() (18)
(18)
При ![]() получим формулу для определения границы возмущенной области
получим формулу для определения границы возмущенной области ![]() без учета влияния начального градиента:
без учета влияния начального градиента:
![]()
Как видно при
Таким образом, в данной статье получены приближенные формулы для определения размера (радиуса) области возмущения с учетом влияния начального градиента методом «усреднений».
Литература:
- Подземная гидравлика. Учебник для вузов. К. С. Басниев., А. М. Власов, И. Н. Кочина, В. М. Максимов. — М.: Недра, 1986. — 303 с.
- Чарный И. А. Подземная гидрогазодинамика. М.: Гостоптехиздат, 1963.
- Г. П. Гусейнов. Некоторые вопросы гидродинамики нефтяного пласта Азербайджанское государственное издательство. Баку — 1961, 232 с.







