Методы и техника моделирования достигли значительных успехов, однако задачи отработки на земле полетных режимов космических аппаратов усложнились, так как усложнились их конструкция и условия полета. Создание моделирующих установок для комплексной отработки натурных образцов космических аппаратов позволяет существенно сократить сроки доводки, снизить суммарные материальные затраты на отработку отдельных систем и космического аппарата в целом, а главное — дает возможность увеличивать надежность работы космического аппарата.
Ключевые слова: калориметрический приемник, термоэлектрические приемники, имитатор, циркуляционный насос термостата.
Для формирования температурного поля основания радиатора необходимо рассчитать требуемые значения локального коэффициента теплообмена αтр на различных участках основания теплообменника. Найдем распределение αтр(x) из дифференциального уравнения пластины при следующих условиях: с одной стороны на основании теплообменника поддерживается постоянная плотность теплового потока qs; тепловой поток с другой уносится протекающим теплоносителем; теплообменом с торцов пренебрегаем; изменение плотности теплового потока за счет теплопроводности по длине каналов пренебрежимо мало; тепловой режим стационарный, начало отсчета — вход в канал:
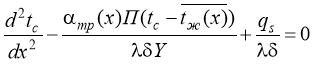 (1)
(1)
Предлагаемый метод позволяет формировать на основании радиатора температурные поля различного вида. Рассмотрим решение уравнения для случая равномерного температурного поля основания, т. е. ![]() =0. Тогда коэффициент теплообмена выражается из уравнения (1):
=0. Тогда коэффициент теплообмена выражается из уравнения (1):
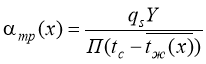 ,(2)
,(2)
где разность температур стенки и жидкости ![]() находится из решения уравнения теплопроводности для ламинарного течения жидкости в плоском канале при постоянной температуре стенки [1]:
находится из решения уравнения теплопроводности для ламинарного течения жидкости в плоском канале при постоянной температуре стенки [1]:
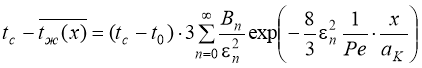 (3)
(3)
На рис.2 представлен результат расчета распределения ![]() по выражению (3) при следующих условиях:
по выражению (3) при следующих условиях: ![]() ,
, ![]() ,
, ![]() =5 мм,
=5 мм, ![]() =1 см/с.
=1 см/с.
С учетом принятых допущений (весь тепловой поток с основания радиатора снимается протекающим теплоносителем) в выражении (2) П=Y, тогда ![]() будет рассчитываться:
будет рассчитываться:
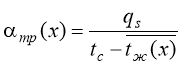 (4)
(4)
Результат расчета представлен на рис. 1. Для реализации такого характера распределения ![]() предлагается воздействовать на интенсивность локального теплообмена изменением высоты ребер: на начальном участке выполнить их с меньшей высотой, а на конечном — с большей, как показано на рис.2. [2]
предлагается воздействовать на интенсивность локального теплообмена изменением высоты ребер: на начальном участке выполнить их с меньшей высотой, а на конечном — с большей, как показано на рис.2. [2]
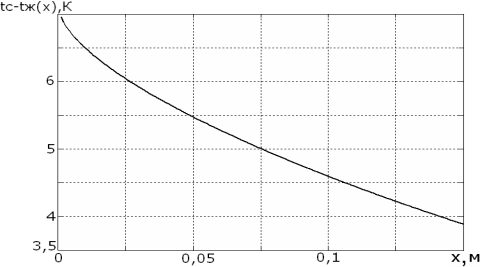
Рис. 1. Разность температуры стенки и среднеобъемной температуры теплоносителя по длине канала ![]()
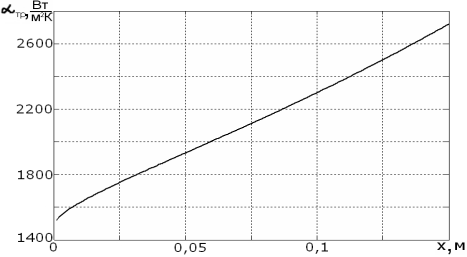
Рис. 2. Распределение требуемых значений коэффициента теплообмена
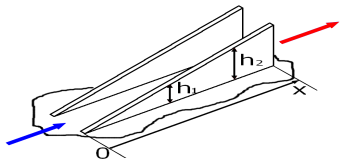
Рис. 3. Переменная высота ребер радиатора
Для расчета необходимой высоты ребер удобно воспользоваться эффективным коэффициентом теплоотдачи ![]() [2], характеризующим интенсивность теплообмена на оребренной поверхности — основании радиатора. Зависимость
[2], характеризующим интенсивность теплообмена на оребренной поверхности — основании радиатора. Зависимость ![]() от высоты ребра h(x) можно найти из соотношений [3]:
от высоты ребра h(x) можно найти из соотношений [3]:
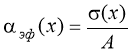 ,(5)
,(5)
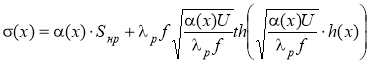 ,(6)
,(6)
где
Необходимое распределение высоты ребер ![]() по длине теплообменника можно найти, решая систему уравнений, составленную из выражений (3), (4), (5), (6):
по длине теплообменника можно найти, решая систему уравнений, составленную из выражений (3), (4), (5), (6):
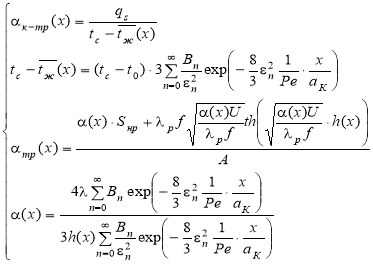 (7)
(7)
Решение системы уравнений (7) проводится численно для участка основания радиатора с одним ребром, окруженным двумя половинками каналов. Ребро разбивалось на элементарные участки длиной dx, шириной равной шагу оребрения (aК+bК), как показано на рис.4:
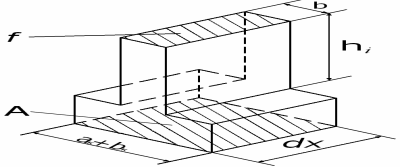
Рис. 4. Элементарный участок ребра
На каждом из участков находилась необходимая высота ребра hi для обеспечения требуемого локального значения ![]() . Процедура расчета повторялась по всей длине ребра.
. Процедура расчета повторялась по всей длине ребра.
Расчет выполнен для экспериментальной установки, описанной в начале настоящей главы, при следующих условиях: теплопроводность дюрали ![]() =164
=164 ![]() , ширина каналов аК=5 мм, толщина ребер bК=2 мм, плотность теплового потока на основании теплообменника qs=10
, ширина каналов аК=5 мм, толщина ребер bК=2 мм, плотность теплового потока на основании теплообменника qs=10 ![]() , температура теплоносителя на входе t0=35 °С, температура основания tc=42 °C, расход теплоносителя G=3,44·10–7
, температура теплоносителя на входе t0=35 °С, температура основания tc=42 °C, расход теплоносителя G=3,44·10–7![]() .
.
Вычисления проводились на языке Matlab. Результаты расчета распределения высоты ребер h(x) по длине основания радиатора показаны сплошной линией на рис.16. Видно, что для обеспечения равномерного температурного поля основания радиатора необходимо изготовить ребра переменной высоты, изменяющейся с 1 мм до 17 мм. Однако изготовление криволинейного (волнообразного) профиля ребра существенно усложняет изготовление радиатора. Значительно упростить трудоемкость фрезеровки можно, если высоту ребра изменять по линейной зависимости. Результат аппроксимации результатов расчета обозначен на рис. 23 пунктирной линией [5]:
![]() (8)
(8)
Для экспериментальной проверки проведенных расчетов основание радиатора экспериментальной установки было доработано следующим образом: Схематическое изображение радиатора представлено на рис.5.
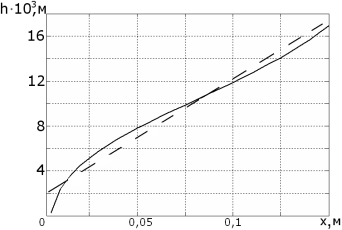
Рис. 5. Результат расчета переменной высоты ребер
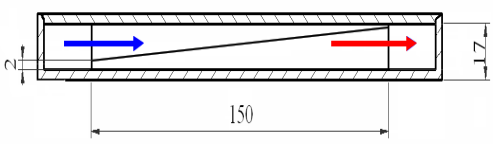
Рис. 6. Теплообменник с переменной высотой ребер
Сверху основание радиатора закрывается симметричной ответной частью. Таким образом, изменение высоты ребер не приводит к изменению площади проходного сечения каналов. Такое конструктивное решение позволяет теплоносителю двигаться с равной скоростью по всей длине основания радиатора. Стык ребер основания и ответной части промазывается слоем гидро-теплоизоляции для исключения теплового контакта.
В результате проведенных экспериментов было установлено, что предложенный метод формирования температурного поля позволил уменьшить градиент температуры по основанию радиатора.
Максимальный градиент температуры составил 0,01 К/см при подаваемой мощности 100 Вт, что подтверждает эффективность предложенного метода формирования температурного поля. [6]
Литература:
- Дульнев Г. Н. Тепло- и масообмен в радиоэлектронной аппаратуре: Учебник для вузов по спец. «Конструир. И произв. радиоаппаратуры». — М.: Высш. шк., 1984. — 247 с., ил.
- ГОСТ 8.338–2002 Преобразователи термоэлектрические. Методика поверки
- Калориметрия. Теория и практика: Пер. с англ./В.Хеммингер,Г.Хёне. — М.: Химия, 1990. — Пер. изд.: ФРГ, 1984. — с. 176.
- Геращенко О. А., Федоров В. Г. Тепловые и температурные измерения. — Киев: Наук. Думка, 1965.-304 с.
- Андрейчук О. Б., Малахов Н. Н. Тепловые испытания космических аппаратов. М.: Машиностроение, 1982, 143 с.
- Гордов А. Н., Парфенов В. Г., Лукьянов Г. Н., Потягайло А. Ю., Шарков А. В., Основы метрологии. Учебное пособие по курсу «Основы метрологии и планирование эксперимента». — Л.: изд. ЛИТМО,1983, с.84.







