В статье рассматривается прямолинейно-параллельный неустановившийся фильтрационный поток упругой жидкости, при заданном забойном давлении во времени. Задача решается методом усреднений [1, 2].
Ключевые слова: упругий, одномерный, начальный градиент, метод «усреднений», приближенный.
The article deals with a straight-parallel unsteady filtration flow of an elastic liquid at a given bottom-hole pressure in time. The problem is solved by averaging [1, 2].
Keywords: elastic, one-dimensional, initial gradient, «averaging» method, approximate.
Предположим, что пласт одномерный, начало координат расположено у галереи, а ось х направлена по длине пласта.
Согласно предположению соответствующее уравнение имеет вид:
![]() (1)
(1)
Применяя метод «усреднений», заменим уравнение (1) приближенным уравнением:
где
![]() (3)
(3)
Граничные условия для данной задачи запишутся в следующей форме:
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
Кроме того, ![]() (7)
(7)
Интегрируя выражение (1), получаем:
![]() (8)
(8)
При х=0 получаем ![]()
При
![]() (9)
(9)
откуда 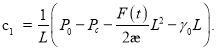 (10)
(10)
Подставляя полученные выражения для ![]() в (8), получаем:
в (8), получаем:
![]() (11)
(11)
![]() находим из условия (7):
находим из условия (7):
![]()
Тогда ![]() откуда
откуда
![]() (12)
(12)
Подставляя (12) в (11), получаем:
![]() (13)
(13)
Находим
![]() (14)
(14)
где ![]()
Подставив выражение (14) в (3), получаем дифференциальное уравнение для определения ![]()
![]()
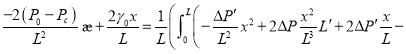
![]() (15)
(15)
Откуда получаем:
![]()
Если учесть, что ![]() после несложных преобразований получаем:
после несложных преобразований получаем:
![]() (16)
(16)
Предположим, что значение ![]() изменяется незначительно. Тогда, можно предположить, что
изменяется незначительно. Тогда, можно предположить, что ![]() Для решения дифференциального уравнения (16) умножим обе части уравнения на
Для решения дифференциального уравнения (16) умножим обе части уравнения на
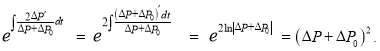
Тогда получим:
![]()
![]()
или
![]()
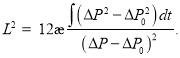 (17)
(17)
При ![]() тогда из (17) получается известная формула
тогда из (17) получается известная формула ![]()
Таким образом, мы получили формулу для определения границы возмущения при прямолинейно-параллельном движении упругой жидкости.
Литература:
- Гусейнов. Некоторые вопросы гидродинамики нефтяного пласта // Азербайджанское государственное издательство. — Баку, 1961. –232с.
- Подземная гидравлика: Учебник для вузов /К. С. Басниев, А. М. Власов, И. Н. Кочина, В. М. Максимов. –М.: Недра, 1986. –303с.







