In this paper we give a proof of Oppenheim’s theorem, and give some related results and problems.
Keywords: triangle, inequality, theorem, Oppenheim theorem, area, L![]() .
.
There are many inequalities for triangles and for their elements (sides, height, bisector, radiuses of the circumscribed and inscribed circles, etc.). In many inequalities the elements of triangles appear symmetrically. Let us denote by ![]() the sides
the sides ![]() the radius of the circumscribed circle, the radius of the inscribed circle, semiperimeter, and area of the triangle
the radius of the circumscribed circle, the radius of the inscribed circle, semiperimeter, and area of the triangle ![]() respectively.
respectively.
For instance,
![]()
![]()
But there are also inequalities which are not symmetric with regard to their elements. For instance, in [3], Parvardi showed that
![]() (1)
(1)
These are often special cases of parametric families of inequalities with parameters not depending on the elements of triangle. For example:
If ![]() then prove that
then prove that
(American Mathematical Monthly in1988)
In these inequalities we use Oppenheim theorem ([1], [2]) and it is very useful for many problems.
[Oppenheim’s theorem] For the triangle ![]() and real numbers
and real numbers ![]() , if
, if ![]() then
then
![]() (2)
(2)
The equality holds if and only if
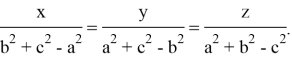
Proof. (based on [2], page 1) Let, ![]() . It is known that,
. It is known that,
![]() so,
so,
![]()
and we get
This inequality is equivalent to
![]() (3)
(3)
We use Cauchy’s theorem for the left-hand side of the inequality (3):
![]() (4)
(4)
we get,
![]()
Use cosine law and ![]() we get result:
we get result:
![]()
By the Cauchy inequality in (4), the equality holds if and only if
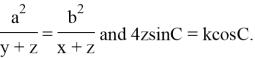
So, as

Then, let
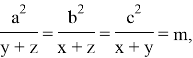
![]()
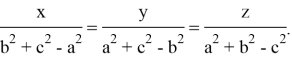
To prove the converse,
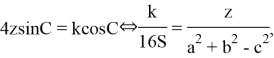
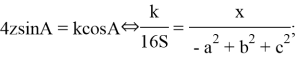
then equality holds in (2) if and only if
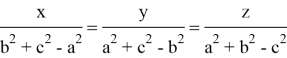
Note that in the theorem the parameters
Now we study new and beautiful results of the theorem. As mentioned above, Pavardi [3] gave the inequality ![]()
Proof. Setting ![]() in (2), the result follows immediately.
in (2), the result follows immediately.
Result.1 Prove that: ![]() , with equality only when
, with equality only when ![]()
Proof. The usual proof of the Euler inequality uses hard geometric constructions and an explicit calculations of the distanse between the centers of the inscribed and circumscribed circles. We know give a quick proof using Oppenheim’s theorem and the well-known identity (see, Problems in plane and solid geometry, [9]) If we take ![]() then by Theorem 0 we have that
then by Theorem 0 we have that
![]()
Squaring both sides and cancelling gives
![]()
Substituting ![]() and
and
![]() (5)
(5)
the result follows.
Result 2 Prove that:
![]()
with equality only when ![]()
Proof. The usual proof of the Leibniz inequality uses hard geometric constructions and an explicit calculation of the distance between the center of the circumscribed circle and centroid of the triangle (see, [9]).Now we prove it algebraically using Theorem 0. Let ![]() ,
, ![]() , and
, and ![]() . We get
. We get
![]()
Substituting (5) we get
![]()
and again the equality holds only when ![]()
Result.3 If ![]() then prove that,
then prove that,
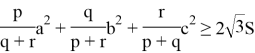
(Problem E3150, Am. Math. Monthly [5])
Proof. If instead of
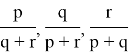
then we can easily check that they satisfy the conditions of the theorem.We get
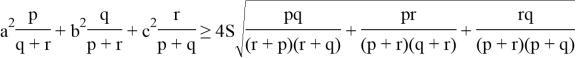
By the Cauchy theorem
![]()
then,
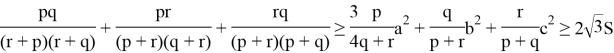
References:
- D.Sachelarie, Geometry of the triangle, Matrix-Rom-Bucuresti, 2000
- Marcel Chirita, Mathematical Excalibur 17(5), 2013, p.1
- Amir Hossein Parvardi, 150 Nice geometry problems, 2011
- Dusan Djukic, Vladimir Jankovich, The IMO Compendium 2010
- G. Tsintsifas, Problem E3150, Amer. Math. Monthly 93(5), 1986, p.400
- Samer Seraj, Geometric Inequalities Marathon 2011, problem 4
- V. E. Olhov, About applying trigonometric functions to demonstrate inequality, Mathematics in School (2), 1979, p.56
- V.Nicula On an inequality in a triangle dinGM8,1984
- Viktor Prasolov translated and edited by Dimitry Leites, Problems in plane and solid geometry, 2001







