В статье рассматриваются вопросы обучения школьников выделению существенных признаков геометрических объектов на основе исследования как методики развития математического мышления у школьников в рамках личностно-ориентированного обучения.
Выделены основные этапы исследования, предложены примеры исследовательских задач, ориентированных на изучение свойств и признаков геометрических объектов.
Ключевые слова: задача, математическое мышление, обобщение результата, процесс решения, условие задачи.
Сегодня, сфера школьного обучения математике рассматривается как возможность обеспечить личностный уровень интеллектуального развития школьников, при условии, если их познавательная деятельность будет приобретать характер поиска, который наделен личностным смыслом и превращающего учащегося из субъекта целостной познавательной деятельности в субъекта отношения в познании.
Личностно ориентированный подход в обучении немыслим без выявления и изучения индивидуальных особенностей каждого ученика.
Использование исследования как методики развития математического мышления у школьников предполагает предварительный анализ самого процесса исследования и дальнейшей его адаптации для средней школы.
Структура научного исследования может быть представлена в следующем виде (рисунок 1):
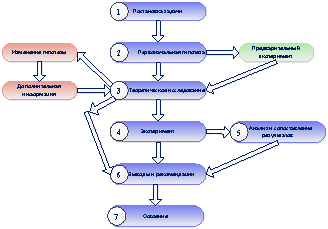
Рис. 1. Структура научного исследования
Как видно из рисунка, стандартно выделяют семь основных этапов проведения научного исследования.
Адаптацию такой сложной схемы проведения исследования для школьников предлагает Аксёнов А. А., в его работе [1] выделяются следующие этапы построения научного исследования:
− постановка задачи;
− предварительный анализ условия, включающий выбор класса задачи;
− выбор метода решения задач определенного класса;
− формулировка гипотезы исследования;
− планирование и организация эксперимента;
− анализ и обобщение результатов;
− формулировка новых фактов и законов;
− получение объяснений или научных предсказаний.
Главной целью такого исследования является открытие на субъективном уровне новых математических знаний, связанных с полученными результатами исследования. Основной проблемой для корректного построения исследовательских задач является их разумный подбор. Исследовательской задачей нельзя считать любую задачу, в которой ученик приобретает новые знаний и навыки. Поэтому возникает необходимость классификации задач, которая может проводится путем обобщения структуры задачи в виде:
где ![]() — определяет собственно условие задачи;
— определяет собственно условие задачи; ![]() — вычленяет требования задачи;
— вычленяет требования задачи; ![]() — описывает искомое решение задачи;
— описывает искомое решение задачи; ![]() — предполагает теоретические основы, которые могут стать базой для решения задачи;
— предполагает теоретические основы, которые могут стать базой для решения задачи; ![]() — определяет способ решения задачи;
— определяет способ решения задачи; ![]() — описывает основное отношение, реализация которого предполагается в процессе решения [2].
— описывает основное отношение, реализация которого предполагается в процессе решения [2].
Классификация математических задач может проводиться достаточно разнообразно, однако наиболее популярным является следующий вариант:
− задачи на поиск некоторого компонента;
− задачи на доказательство указанного утверждения;
− задачи, предполагающие в качестве результата некоторое построение;
− исследовательские задачи;
− конструктивные задачи;
− задачи, результатом которых должно быть приведение конкретного примера реализации условия;
− задачи, решение которых предполагает словесное описание.
Используя формальное описание структуры задачи (1) можно говорить о том, что основные задачи, используемые в школьном курсе, относятся к алгоритмическим. Такие задачи предполагают исключительно поиск неизвестного ![]() , при этом нет необходимости расширять объем полученных знаний, так как весь теоретический материал
, при этом нет необходимости расширять объем полученных знаний, так как весь теоретический материал ![]() , требуемый для решения, излагается в рамах учебной программы.
, требуемый для решения, излагается в рамах учебной программы.
Конечно, для развития одаренных детей такие задачи неинтересны, в них не может быть отражен исследовательский процесс, так как заранее известны все компоненты. Поэтому выделяются полуэвристические и эвристические задачи. В полуэвристических задачах заранее неизвестен метод решения или даже не точно выделено искомое. Если же в рамках задачи строго определено исключительно условие и требования, то такие задачи становятся эвристическими, это не строго определяет факт использования только эвристического метода решения, но предполагает и технологию поиска такового решения.
Следуя этому правилу, все задачи школьного курса геометрии можно распределить на несколько групп:
задачи, предполагающие решение при помощи стандартных алгоритмов;
задачи, в рамках решения которых используются стандартные методы и алгоритмы;
задачи, решение которых может быть сведено к стандартным известным методам после некоторого преобразования;
задачи, решение которых не может проводиться при помощи стандартных методик, а предполагает использование общих технологий решения задач.
Задачи на исследование обладают характерными чертами, которые могут быть сформулированы следующим образом:
в рамках задачи необходимо:
найти условия, при которых будет истинным и ложным определенный факт;
сформулировать самостоятельно факт, истинность или ложность которого нужно доказать;
определить свойства некоторого геометрического объекта и условия, при которых эти свойства будут выполняться;
определить наличие определённых свойств у геометрического объекта с обязательным формированием альтернативных гипотез на принадлежность этих свойств объекту;
определить признаки геометрического объекта в определенных условиях.
Примерами исследовательских задач, ориентированных на изучение свойств и признаков геометрических объектов могут служить [3]:
- Задача о вписанной окружности.
- Задача о медианах.
- Задача про геометрическое место точек площади.
- Задача о шаблоне.
Решение таких задач обязательно предполагает последовательность действий, которые аналогичны этапам проводимых научных исследований. Ключевым свойством таких задач является необходимость разложения на подзадачи, каждая из которых требует доказательства или поиска определенных компонентов геометрических объектов.
Анализ задачи превращается в последовательный процесс изучения всех возможных ситуаций, которые связаны с сопоставлением свойств геометрических объектов, описанных в условии задачи. Следовательно, такие задачи относятся к эвристическим и могут применяться для школьников начиная с 5–6 класса, когда уже идет формирование логического мышления.
Методология введения таких задач в учебный процесс должна обязательно предполагать следующие этапы:
- Знакомство с исследовательскими задачами и изложение принципа самого исследования, который предполагает обязательное выделение необходимых этапов.
- Описание разделения задач на классы, и демонстрация на примерах вариантов отнесения задач к разным классам. Акцентирование внимания на корректное отнесения задачи к определенному классу, что влечет за собой выбор вариантов решения.
- Развивать исследование постепенно только после освоения технологии работы с задачами такого типа и усвоением методов решения.
- Проводить обобщение результатов и формировать новые более сложные гипотезы, которые могут стать основной для проектного исследования в дальнейшем.
- Предлагать формулировку вопросов, а не вариантов решений и алгоритмов их проведения.
В качестве примера геометрической задачи, которая после анализа условия вряд ли будет рассмотрена как исследовательская, однако становится таковой в процессе решения, можно рассматривать задачу о треугольнике, отсекаемом касательной или проект «Изучение свойств ромба».
Начальный уровень усвоения методики работы с исследовательскими задачами предполагает разбиение задачи на подзадачи, которые описывают разные ситуации, возникающие на основе соотношений между характеристиками геометрических объектов (окружностей).
Развитие математического мышления и обучение математике необходимо проводить цельно, так как только поступательно, опираясь на уже полученные знания, ученик может освоить сложные разделы геометрии, которые включают понятия о пространстве и основных постулатах его построения.
При этом школьник привыкает к специализированным приемам и технологиям, которые используются в конкретных методических программах. К сожалению, нет достаточно развитого курса, который не просто направлено идет от основной школы и на ее базе формирует знания начиная от младшего школьного возраста и заканчивая старшей школой. Это отчасти связано с тем, что таких сквозных учебников было мало и не все получили достаточно высокую оценку от учителей.
Литература:
- Аксёнов А. А. Математическая задача как средство выполнения учебных исследовании в средней школе и отдельный вид задач на исследование // Ученые записки ОГУ. Серия: Гуманитарные и социальные науки. 2016. № 4 (73).
- Аксёнов А. А. Сущность эвристических математических задач и специфика их использования в обучении школьников // Ученые записки ОГУ. Серия: Гуманитарные и социальные науки. 2015. № 6 (69). — С. 219–223.
- Ручкина В. П. Курс лекций по теории и технологии обучения математике в начальных классах: учеб. пособие. — Екатеринбург: ФГБОУ ВО «Урал. гос. пед. ун-т», 2016. — 313 с.







