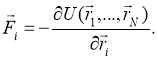Цель данной статьи — изучение распределения плотности в DPPC-мембране, используя силовое поле Martini.
Ключевые слова: DPPC мембрана, метод молекулярной динамики, силовое поле Martini, плотность.
Введение
Как известно, биологические мембраны выполняют множество функций, таких как транспортная, барьерная, рецепторная и т. д. [1] В данной работе мы уделим внимание транспортной функции биологической мембраны. Транспорт обеспечивает: создание ионных градиентов, доставку питательных веществ, поддержание приемлемого pH и т. д.
Как правило, биологические мембраны образуются слоем липидов, одним из распространенных видов липидов в биологических мембранах является липид DPPC. Монослой, образованный поверхностно-активным веществом легких на границе раздела, состоит в основном из фосфолипидов (80 %), белков (12 %) и нейтральных липидов (8 %). Среди этих фосфолипидов преобладает фосфатидилхолин (PC или лецитин) (70–85 %), который составляет пул, в котором 50 % материала составляет DPPC. [2]
Полагается, что приложение внешнего электрического поля способствует образованию поры в мембранной структуре.
Поры в мембранах, образованные благодаря электрическому полю (электропорация), могут стать предметом для исследования. Электропорация обычно используется в молекулярной биологии и биотехнологии и недавно нашла применение в медицине, изучался транспорт лекарственных средств через мембрану [3–7].
Методы
Дипальмитоилфосфатидилхолин (DPPC) — фосфолипид из группы насыщенных фосфатидилхолинов, один из главных компонентов лёгочного сурфактанта. В моделях биологических мембран часто используется именно данный липид [8]. Липид обычно состоит из полярной головки и липидного хвоста [9]. На рисунке (1) представлено схематическое представление бислоя DPPC:
Рис. 1. Схема DPPC бислоя
При приложении электрического поля вдоль мембраны, мембрана деформируется, в мембране образуются поры [10].
Расчет процессов в мембранах производиться с помощью метода молекулярной динамики (МД). В основе метода МД представлена модель многоатомной молекулярной системы, в которой все атомы представлены материальными точками, движение которых описывает уравнение Ньютона. Таким образом, имеется система, состоящая из N точечных частиц, каждая из которых имеет массу, скорость и радиус-вектор 
.
Численное решение системы классических уравнений движения:
|
|
(1) |
где 
— масса i-ой частицы, N — число частиц. Левая часть уравнения (1), есть произведение массы на ускорение, где:
|
|
(2) |
Уравнение (1) есть не что иное, как представление второго закона Ньютона, для системы, состоящей из N числа частиц.
Граничные условия системы задаются уравнениями (3):
|
|
(3) |
Свойства системы определяются выбором потенциала:
|
|
(4) |
Рассмотри поведение при постепенном сближении двух частиц. На очень большом расстоянии частицы не взаимодействуют. По мере сближения частиц между ними возникает сила притяжения. Она постепенно увеличивается и достигает некоторого максимального значения, а затем частицы начинают отталкиваться друг от друга.
Таким образом, получаем, что зависимость энергии взаимодействия между частицами от расстояния r, аналогично кривой потенциальной энергии двух молекул. Каждой точке потенциальной кривой соответствует потенциальная энергия неподвижной системы из двух частиц, находящихся на расстоянии r друг от друга.
Электрическое поле
в системе не эквивалентно приложенному полю, а рассчитывается из соображений:
, (5)
где 
— приложенное внешнее электрическое поле, 
— поле деполяризации, поле, которое создается за счет поляризации среды.
Молекулярно-динамическое моделирование
Для моделирования мембраны выбрано силовое поле martini22p, полярные аминокислоты Martini 2.2, липиды Martini 2.0 и поляризуемая вода. Количество липидов 512 (256 липидов на каждый слой), имеется водяной слой с обеих сторон мембраны.
Создавался файл равновесия, в котором мембрана приводилась к состоянию равновесия рисунок 2.
Рис. 2. Бислой липидов DPPC
Бислой мембраны DPPC окружен молекулами воды в системе обозначен как PW (pure water).
Затем вдоль оси z (поперек) мембраны было приложено электрическое поле E=0,3 B/нм. Время моделирования системы 300 нс. Динамика поведения DPPC мембраны под действием электрического поля представлена на рисунке 3.
Рис. 3. Динамика подвижности DPPC липидов под действием электрического поля.
Полости, которые представлены на рисунке 3, заполнены молекулами воды, для рассмотрения полостей, образованных за счет электрического поля, мы удалили молекулы воды на изображении.
Разделим время моделирования на 6 равных частей и определим плотность в каждый момент времени рисунок (4):
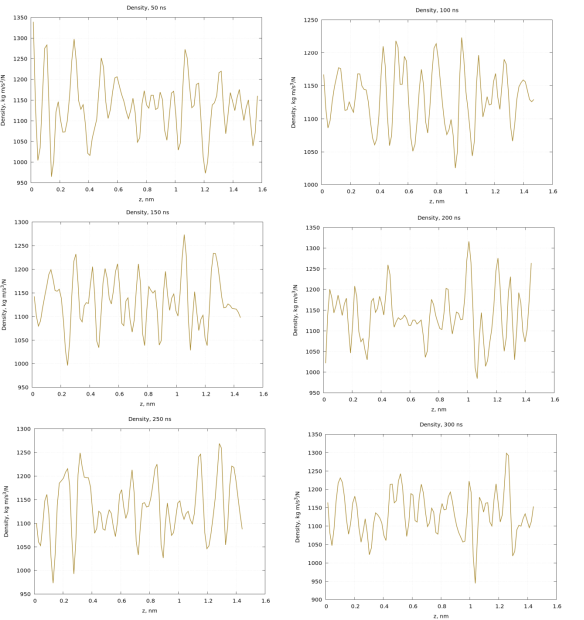
Рис. 4. Плотность частиц DPPC мембраны в различные моменты времени
Заключение
В исследовании была построена модель двухслойной мембраны DPPC по 256 липидов на каждый слой, окруженная молекулами воды. Было выбрано силовое поле martini22p. Рассчитана плотность частиц в DPPC мембране. Рассмотрено плотность распределения частиц в моменты времени: 50, 100, 150, 200, 250, 300 нс.
Исследования показали, что при приложении внешнего электрического поля вдоль мембраны, образуются поры, сквозь которые могут диффундировать молекулы воды.
Рисунок 4 показывает, что плотность числа частиц в различные моменты времени всегда различна и имеет синусоидальный характер.
Рисунок 3 показывает, что в различные моменты времени липиды принимают различное положение.
Исследование по данной тематике будет продолжено.
Литература:
- Твердислов В. А., Яковенко Л. В. Физика биологических мембран // Акустика. Теория относительности. Биофизика. — М., Просвещение, 1990. — С. 131–158
- Stachowicz-Kuśnierz, Anna; Seidler, Tomasz; Rogalska, Ewa; Korchowiec, Jacek; Korchowiec, Beata (2020–02–01). «Lung surfactant monolayer — A good natural barrier against dibenzo-p-dioxins». Chemosphere. 240.
- L. Sukit, K. S. Amadeu. Molecular Simulation Study of Structural and Dynamic Properties of Mixed DPPC/DPPE Bilayers // Biophys. J. — 2009. — V. 90. — C. 3951–3965.
- R. Jahn, H. Grubmu. Membrane fusion // Curr. Opin. Cell Biol. — 2002. — 14: C. 488–495.
- M. Dyck, P. Kruger, M. Losche. Headgroup organization and hydration of methylated phosphatidylethanolamines in Langmuir monolayers // Phys. Chem. Chem. Phys.- 2005. — 7. — C. 150–156.
- M. Tarek. Membrane Electroporation: A Molecular Dynamics Simulation // Biophys. J. — 2005. — V. 88. — C. 4045–4053.
- T. J. Lewis. A model for bilayer membrane electroporation based on resultant electromechanical stress // IEEE Trans. Dielec. Elec. Insul.- 2003. — 10. — C. 769–777.
- Y. Qianqian, S. Xinyuan, D. Haiou, D. Xingxing, W. Guang, O. Yanjiang. Interactions of Borneol with DPPC Phospholipid Membranes: A Molecular Dynamics Simulation Study // Int. J. Mol. Sci. — 2014. — 15. — C. 20365–20381.
- G. F. Chen, Y. Y. Chen,, N. N. Yang,, X. J. Zhu, L. Z. Sun, G. X. Li. Study of the interaction between curcumin and mimetic biomembrane // Sci. China Life Sci. — 2012. — 55. — C. 527–532.
- C. A. López, Z. Sovova, F.J. van Eerden, S. J. Marrink. Martini force field parameters for glycolipids // J. Chem. Theory Comput. 2013, 9, 1694–1708.
