Повышение безопасности в пороговой схеме разделения секрета Шамира при помощи использования модульной арифметики



Ключевые слова: информация, защита информации, пороговые схемы разделения секрета, схема Шамира.

Защита информации — деятельность, направленная на предотвращение утечки защищаемой информации, несанкционированных и непреднамеренных воздействий на защищаемую информацию [1, с. 1].

В настоящее время защите информации уделяют немало времени и ресурсов, и это правильно, ведь она представляет значительную ценность. С этой целью используются различные криптографические методы. В число таких методов входят и пороговые схемы разделения секрета.

Пороговая схема разделения секрета представляет из себя такую (k, n) схему, в которой секрет делится между участниками в количестве «n» и для восстановления секрета требуется любая группа из не менее, чем «k» участников. Обязательным условием для пороговых схем является неравенство: k < n.

Далее рассмотрим первоначальный вариант пороговой схемы разделения секрета Шамира и продемонстрируем, как модульная арифметика позволяет повысить безопасность.

Идея схемы Шамира заключается в том, что для интерполяции многочлена, степень которого k-1, требуется k точек. Если число известных точек меньше k, то интерполяция невозможна.

Если мы рассматриваем полином первой степени, например f(x) = x+4, то для того, чтобы построить эту функцию нам понадобится минимум две точки. Если полином будет второй степени, например f(x) = x²+5x+3, то для построения графика такой функции потребуется, по крайней мере, три точки и так далее.

Теперь более подробно рассмотрим, как происходит разделение и восстановление секрета.

1) Разделение секрета

Предположим, что наш секрет S равен 42. Превращаем данное число в точку на декартовой системе координат (0,42). Затем требуется придумать такую полиномиальную функцию, которая бы удовлетворяла данной точке, и степень которой была бы k-1, где k — порог требуемых долей секрета, для его восстановления. Полином будет иметь вид f(x)=a₀+a₁x+a₂x²+…+a_k-1x^k-1, где:

• a₀ =S;
• a₁,a₂,…,a_k-1 — положительные целые числа, которые выбираются случайным образом.

Для нашего примера примем пороговое значение долей для восстановления секрета k=3, всего же будем генерировать 5 долей секрета. Наша полиномиальная функция будет следующая: f(x) = 42+3x+5x². Далее раздаём 5 фрагментов секрета, при условии, что x не равен 0, поскольку это наш секрет. Получаем следующие фрагменты: (18, 1716), (23,2756), (27, 3768), (31, 4940) и (35, 6272) и отправляем по одному фрагменту каждому из пяти хранителей «ключа». Стоит заметить, что k=3 является открытой информацией.

2) Восстановление секрета

Если любые трое из пяти доверенных лиц хотят восстановить секрет S, тогда им нужно восстановить полином, используя свои доли. Для этого они с помощью своих точек, пусть это будут: (18, 1716), (23,2756), (27, 3768), должны рассчитать интерполяционный полином Лагранжа, используя следующие формулы:

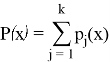
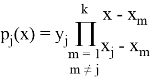
В нашем случае это будет выглядеть следующим образом:

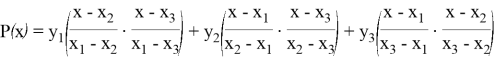
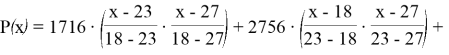
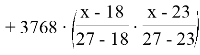
В итоге получаем:

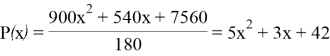
Поскольку нам известно, что S=P(0), то восстановление секрета осуществить просто:

Но такая идея разделения секрета имеет существенную проблему, которая заключается в том, что с увеличением числа известных злоумышленнику точек, остаётся меньшее количество значений для других точек. Это противоречит основному свойству таких схем, которое гласит, что злоумышленник не должен получать никаких сведений о значении секрета, если ему известно k-1 и меньше фрагментов этого секрета, в том смысле, что все возможные значения секрета должны быть равновероятны. В нашем же случае это не так.

Чтобы показать это наглядно, рассмотрим ситуацию, когда злоумышленнику стали известны две точки (18, 1716) и (23,2756), а так же он знает открытую информацию, что k=3. Исходя из известной ему информации, он может вывести полином второй степени и подставить известные ему значения:

Затем злоумышленник может узнать значение коэффициента a₁, вычислив разность между f(23) и f(18):

Так как наши коэффициенты a₁,a₂,…,a_k-1 являются целыми положительными числами, то число возможных вариантов значения коэффициента a₂ сводится к минимуму. То есть злоумышленнику становится известно, что a₂ может принимать следующие значения: 1, 2, 3, 4 и 5, поскольку, если a₂ будет больше 5, то коэффициент a₁ станет отрицательным, а это невозможно. Затем злоумышленник может, подставив значение a₁, вывести формулу для вычисления секрета, например для точки (23,2756):

Учитывая, что число вариантов для коэффициента a₂ ограниченно становится понятно, что подобрать и проверить значение секрета S не составит труда.

Для устранения этой проблемы Шамиром было предложено использование модульной арифметики. Суть заключается в замене f(x) на f(x)mod p, где p принадлежит множеству простых чисел, а также p > S и p > n. Это простое число p является порядком конечного поля, то есть поля, элементами которого являются целые числа 0, 1, 2,…, p-1, а все математические операции в этом поле производятся по модулю p.

Продемонстрируем, как это повысит безопасность схемы. В качестве p будем использовать число 79. Оно является простым и больше секрета и числа участников, между которыми делится секрет, следовательно, удовлетворяет всем условиям. Наш полином принимает вид:

Поскольку полиномиальная функция изменилась, то фрагменты (точки) так же примут новый вид: (18,57), (23, 70), (27, 55), (31, 42) и (35, 31). Пусть первые трое участников решили восстановить значение секрета. Для восстановления рассчитаем интерполяционный полином Лагранжа. Поскольку значение секрета находится при x=0, воспользуемся немного изменёнными формулами:

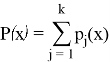
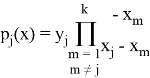
Тогда получим:

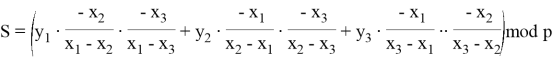
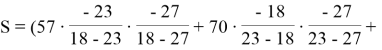
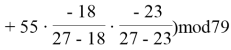
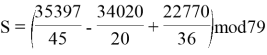
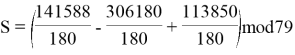
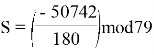
После решения полученного выражения получаем, что S=42. Таким образом, значение секрета восстанавливается. Теперь разберёмся, как модульная арифметика позволяет повысить безопасность.

Допустим, кроме публичной информации k=3 и p=79, злоумышленнику стали известны два фрагмента (18,57) и (23, 70). На основе имеющиеся у него информации он может вывести следующие формулы, где q_x — коэффициент f(x), который показывает целочисленную часть результата деления f(x) на 79:

Теперь злоумышленник может найти значение a₁, вычислив разность между f(23) и f(18):

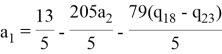
Далее он может попытаться вывести значение S, подставив a₁:

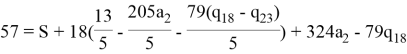
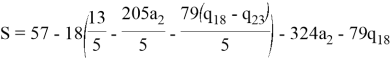
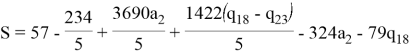
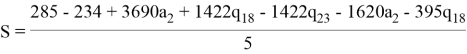
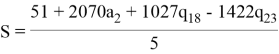
На этот раз злоумышленник столкнётся с серьёзной проблемой, ему, кроме неизвестного секрета S, будут так же неизвестны значения a₂,q₁₈ и q₂₃. Поскольку, возможно бесконечное число различных комбинаций этих параметров, то он не сможет получить никаких сведений о значении секрета. Следовательно, можно сделать вывод, что модульная арифметика исключает проблему описанную ранее.

Таким образом, можно сделать вывод, что использование модульной арифметики исключает проблему, описанную ранее, и позволяет повысить безопасность. А поскольку пороговые схемы разделения секрета применяются для защиты информации, то это только положительным образом сказывается на их конкурентоспособности с другими криптографическими методами.

Литература:

1. ГОСТ Р 50922–2006 Защита информации. Основные термины и определения. — М.: Стандартинформ, 2008. — 12 с.
2. Зыбкин А. Ю. Исследование эффективности применения схемы разделения секрета Шамира в области информационной безопасности: диплом. работа. Санкт-Петербургский государственный морской технический университет, СПб, 2019.
3. Adi Shamir. How to Share a Secret/ Adi Shamir// Massachusetts Institute of Technology. — 1979. — Ноябрь. — c. 612–613