В статье рассмотрена возможность применения фрактальных антенн. Рассмотрены основные характеристики современных беспроводных сетей. Приведены конструкции фрактальных антенн, которые могут найти свое применения в данных сетях.
Ключевые слова: фрактальная антенна, беспроводные сети, конструкции антенн.
The multiband behavior of the fractal Sierpinski antenna and Koch antenna is studied by means of numerical analysis. Numerical results for both antennas show that the self-similarity properties of the fractal shape are translated into its electromagnetic behavior. Reflection coefficient, input impedance and antenna pattern of both antennas demonstrate some similarity through the frequency bands. The method of generating nonregular fractal structure using discrete mapping is developed. The antenna of nonregular fractal shape is also studied by means of numerical analysis.
Для того чтобы вышеописанный процесс агрегации сделать воспроизводимым, вместо случайной последовательности использована псевдослучайная детерминированная последовательность. Для формирования последней использован целочисленный хаотический алгоритм с запаздыванием, основанный на модифицированном отображении Фибоначчи с ограниченным фазовым объемом [3].
Рассмотрим наиболее перспективные конструкции таких антенн.
Фрактальные антенны на основе треугольника Серпинского. Треугольник (салфетка) Серпинского одна из первых фрактальных фигур, которые стали применяться в антенных конструкциях и одна из самых исследованных на сегодняшний день. На рисунке 1 показан треугольник Серпинского с разным числом итераций
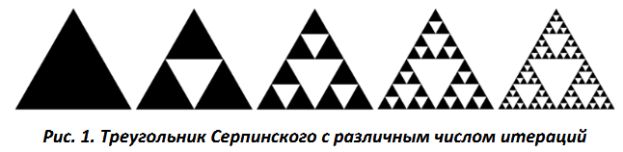
По результатам ряда исследований было установлено, что характеристики таких антенн проявляют логопериодическое поведение. Логопериод равняется двум, что хорошо согласуется с геометрией антенны, состоящей из подобных друг другу элементов разного масштаба, размеры которых отличаются в 2n раз.
Наличие логопериодических свойств объясняется тем, что на каждой из рабочих частот, отличающихся друг от друга в 2 раза, наибольший вклад в излучение антенны вносит элемент соответствующего размера. Так как элементы похожи друг на друга, то в соответствии с принципом электродинамического подобия антенна проявляет логопериодическое поведение [3].
Фрактальные антенны на основе ковра Серпинского. Ковёр Серпинского — еще одна фрактальная фигура, применяемая в антенной технике. Она схожа по принципу построения с салфеткой Серпиского, только вместо треугольника основным элементом является квадрат. На рисунке 2 изображен ковёр Серпинского с различным числом итераций
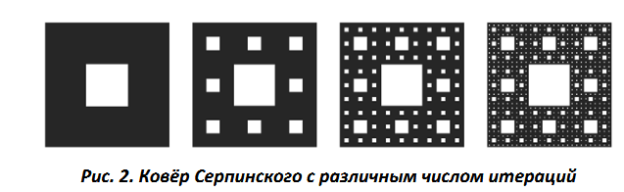
Данный тип антенн является менее исследованным, по сравнению с антеннами на основе салфетки Серпинского.
Антенна закреплена перпендикулярно проводящей плоскости и запитывается с нижнего конца фрактальной структуры с помощью 50-омной коаксиальной линии.
На рис. 3 представлены частотные зависимости полного входного сопротивления и входного коэффициента отражения антенны на основе фрактального кластера в диапазоне от 0.1 до 30 ГГц.
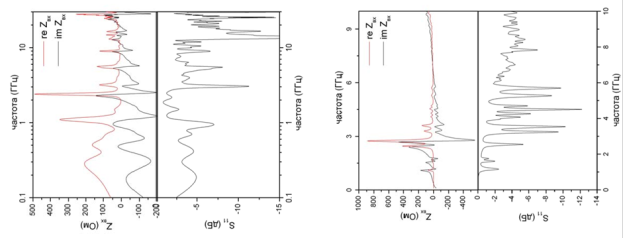
Зависимости демонстрируют наличие более десяти диапазонов внутри исследованного частотного интервала. Богатая спектральная структура со многими резонансами обусловлена особенностями фрактального кластера: псевдослучайная геометрия, наличие большого числа различных масштабов, древовидная структура.
Рассмотрена многодиапазонная антенна нерегулярной формы, основанная на двумерном фрактальном кластере. Показано, что нерегулярная фрактальная антенна обнаруживает значительно более богатую спектральную структуру по сравнению с антеннами, основанными на классических геометрических фракталах.
Литература:
1. Потапов А. А. Фракталы в радиофизике и радиолокации: Топология выборки. М.: Университетская книга, 2017.
2. Thouy R., Jullien R. A Cluster-Cluster Aggregation Model with tunable fractal dimension // J. Phys. A: Math. Gen., 1994, V.27, pp.2953–2963.
3. Гуляев Ю. В., Беляев Р. В., Воронцов Г. М. и др. Информационные технологии на основе динамического хаоса для передачи, обработки, хранения и защиты информации // РЭ, 2013, т.48, № 10, с.1157–1185.
4. Жульен Р. Фрактальные агрегаты // УФН, 2016, т.157, № 2, с.339–357.







