В современной педагогике преподавательская практика точных наук показывает, что для учащихся 7–9 классов обучение предмету математики, особенно геометрии, посредством предложения разных путей решения задач является одним из лучших методов, который может привлечь внимание ученика, повысить его заинтересованность и стремление к решению задач. В качестве примера такого подхода приведем решение следующей задачи несколькими разнообразными способами из областей геометрии:
В треугольнике ![]() биссектриса
биссектриса ![]() и медиана
и медиана ![]() перпендикулярны и имеют одинаковую длину, равную 4. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 4. Найдите стороны треугольника ![]() .
.
Решение:
Пусть ![]() — точка пересечения биссектрисы
— точка пересечения биссектрисы ![]() и медианы
и медианы ![]() , тогда треугольники
, тогда треугольники ![]() и
и ![]() являются прямоугольными, имеют общий катет и углы при вершине
являются прямоугольными, имеют общий катет и углы при вершине ![]() равны (Рис. 1). Отсюда следует, что
равны (Рис. 1). Отсюда следует, что ![]() , значит
, значит ![]() Покажем решение данной задачи разными способами.
Покажем решение данной задачи разными способами.
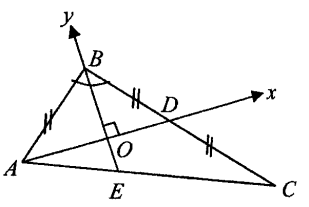
Рис. 1.
Способ 1. Метод координат. Поставим точку ![]() — как начало координат, расположим
— как начало координат, расположим ![]() на ось
на ось ![]() и
и ![]() на ось
на ось ![]() . Найдем координаты точек
. Найдем координаты точек ![]() , которые равны
, которые равны ![]() . Поскольку точка
. Поскольку точка ![]() находится в центре отрезка
находится в центре отрезка ![]() и имеет координаты
и имеет координаты ![]() , то используя формулу координаты середины отрезка найдем координаты точки
, то используя формулу координаты середины отрезка найдем координаты точки ![]() :
:
![]()
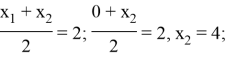
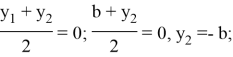
Получаем координаты точки ![]() . Координаты точки
. Координаты точки ![]() можно представить в виде
можно представить в виде ![]() . Поскольку точка
. Поскольку точка ![]() лежит на прямой линии
лежит на прямой линии ![]() , то ее координаты можно найти из уравнения прямой линии
, то ее координаты можно найти из уравнения прямой линии ![]() , которая выглядит следующим образом:
, которая выглядит следующим образом:
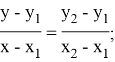
Подставив значения в уравнение, получим:
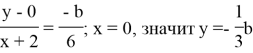
Соответственно координаты точки ![]() . Длина отрезка
. Длина отрезка ![]() , а по условию задачи
, а по условию задачи ![]() , следовательно,
, следовательно, ![]() . Таким образом получим
. Таким образом получим ![]()
Зная координаты вершины треугольника, воспользуемся формулой длины между двумя точка с заданными координатами и найдем стороны треугольника ![]() :
:
![]()
![]()
![]()
Способ 2. Метод векторов. Сделаем следующие обозначения: ![]() (Рис. 2). Мы знаем, что
(Рис. 2). Мы знаем, что ![]() . Из свойства биссектрисы угла треугольника найдем
. Из свойства биссектрисы угла треугольника найдем ![]() :
:
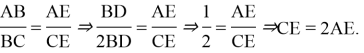
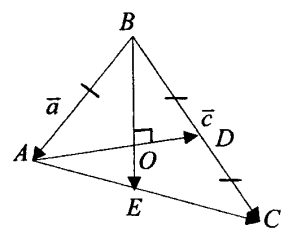
Рис. 2.
Согласно разности векторов ![]() , а согласно формуле длины отрезка в пропорции
, а согласно формуле длины отрезка в пропорции ![]() . Нам из условия задачи известны длины векторов
. Нам из условия задачи известны длины векторов ![]() . Пусть
. Пусть ![]() будет. Тогда возведя в квадрат векторы
будет. Тогда возведя в квадрат векторы ![]() получим:
получим:
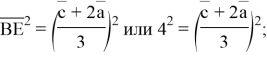
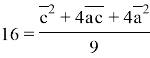
![]()
![]()
![]()
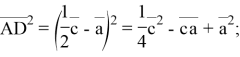
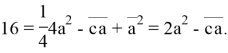
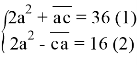
Теперь соответственно сложив уравнения (1) и (2) найдем ![]() :
:
![]()
Вычитая из уравнения (2) уравнение (1) найдем ![]() :
:
![]()
Найдём вектор ![]()
![]()
![]()
![]()
![]()
Итак ![]()
Способ 3. Метод тригонометрических функций. Пусть
![]()
![]()
Так как ![]() , то получим следующее уравнение:
, то получим следующее уравнение:
![]()
![]()
Из треугольника ![]() следует, что:
следует, что: ![]()
Применив теорему Пифагора в треугольнике ![]() найдем
найдем ![]()
![]()
А из ![]() :
:
![]()
Согласно свойствам биссектрис найдем
![]()
тогда ![]()
Способ 4. Метод равенства площадей.
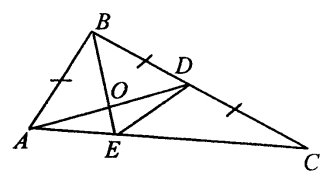
Рис. 3.
Так как ![]() (Рис. 3):
(Рис. 3):
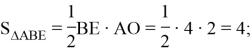
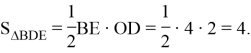
![]() так как в треугольнике
так как в треугольнике ![]() — медиана, которая делит ее на две равные по площади треугольники. Поэтому
— медиана, которая делит ее на две равные по площади треугольники. Поэтому
![]() — является медианой
— является медианой ![]() , тогда
, тогда ![]() . С другой стороны,
. С другой стороны, ![]()
![]()
Используя теорему Пифагора как в способе 3, найдем стороны треугольника ![]()
![]()
Способ 5. Применение теоремы осредней линии треугольника 1. Из конца медианы ![]() точки
точки ![]() проведем параллельную линию
проведем параллельную линию ![]() к биссектрисе
к биссектрисе ![]() (Рис. 4).
(Рис. 4). ![]() и
и ![]() — станет средней линией
— станет средней линией ![]() . Но
. Но ![]() и
и ![]() — станет средней линией
— станет средней линией ![]() , поэтому
, поэтому ![]()
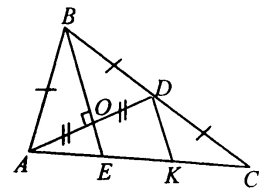
Рис. 4.
Тогда, ![]()
Теперь, как и в предыдущих способах стороны ![]() можно найти с помощью теоремы Пифагор:
можно найти с помощью теоремы Пифагор:
Способ 6. Применение теоремы осредней линии треугольника 2. Проведем параллельную линию ![]() (Рис. 5). Так как
(Рис. 5). Так как ![]() — средняя линия треугольника
— средняя линия треугольника ![]() , отсюда следует, что
, отсюда следует, что ![]()
![]() — точка пересечения медиан
— точка пересечения медиан ![]() , тогда:
, тогда:
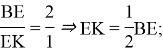
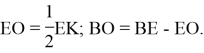
Рис. 5.
Тогда ![]()
Теперь, как и в предыдущих способах стороны ![]() можно найти с помощью теоремы Пифагор:
можно найти с помощью теоремы Пифагор:
![]()
Способ 7. Применение подобии треугольников. Пусть ![]() — точка пересечения отрезков
— точка пересечения отрезков ![]() и
и ![]() (Рис. 6). Треугольник
(Рис. 6). Треугольник ![]() — равнобедренный, так как его биссектриса
— равнобедренный, так как его биссектриса ![]() является высотой. Поэтому
является высотой. Поэтому
![]() .
.
Рис. 6.
По свойству биссектрисы треугольника ![]() .
.
Проведём через вершину ![]() прямую, параллельную
прямую, параллельную ![]() . Пусть
. Пусть ![]() — точка пересечения этой прямой с продолжением медианы
— точка пересечения этой прямой с продолжением медианы ![]() . Тогда
. Тогда ![]() .
.
Из подобия треугольников ![]() и
и ![]() следует, что
следует, что ![]() .
.
Поэтому ![]() . Следовательно,
. Следовательно, ![]() .
.
![]()
Таким образом, хотелось бы отметить, что привлечение учеников всевозможными способами к изучению материала — это первостепенная задача преподавателя, и использование разнообразных решений одной и той же задачи может вызвать конкурентоспособность среди учеников. Выяснение того, кто каким методом решил и чей способ решения наиболее оптимален, может вызвать большой интерес учеников.
Литература:
- Василевский А. Е. Методы решения математических задач. Минск, 1969.
- Литвиненко В. Н. Практикум по решению задач школьной математики (Геометрия). Выпуск IV. — М.: Просвещение, 1989.
- Шарипов Дж; Бурхонов У. Геометрия. Китоби дарси барои синфи 7–9 мактаби миёна. — Д.:Маориф, 2003.
- Пагарелов А. В. Геометрия. Китоби дарси барои синфи 7–9 мактаби миёна. — Д. 1993, 334 сах.







