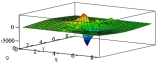
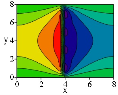
В статье описывается применение аналитического метода расчета пластин с нарушениями регулярности в виде ребер при воздействии сосредоточенных нагрузок. Для аппроксимации локальных влияний используются разрывные функции, что позволяет определять компоненты напряженно-деформированного состояния с такой же точностью, как и в зоне плавного изменения нагрузки. Уравнение изгиба пластин решается методом Власова-Канторовича. Выполнены расчеты прогибов, моментов и перерезающих сил для различных схем загружения пластины. Результаты расчетов при удержании малого числа членов ряда сравниваются с результатами, полученными методом конечных элементов.
При проектировании перекрытий, в выполнении технологических и архитектурных требований, таких как размещение оборудования, обустройство мезонинов в локальных областях, перед конструкторами ставится задача усиления данных зон, например, вводом или изменением геометрии уже существующих ребер жесткости.
Большинство современных программных комплексов основаны на применении метода конечных элементов (МКЭ). При вычислении усилий и моментов в зонах приложения локальных нагрузок из-за высоких градиентов полей напряжений при применении МКЭ требуется существенно сгущать сетку разбивки, что значительно повышает порядок системы разрешающих уравнений. Кроме того, МКЭ позволяет осуществить лишь численный анализ, без получения аналитической зависимости между нагрузкой, геометрическими размерами и напряжением.
В отличии от МКЭ методы расчета конструкций с использованием разрывных импульсных функций позволяют получить аналитические выражения для решения задач с областями нарушения регулярности внутренней геометрии зон приложения полосовой или сосредоточенных нагрузок и рассматривать плиту перекрытия как единый элемент.
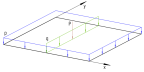
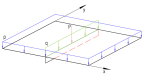
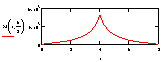
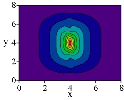
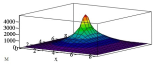
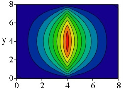
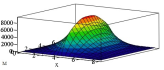
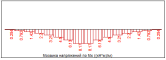
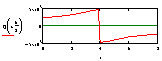
Рассмотрим пластину под действием нагрузки вдоль линии q, сосредоточенной P и распределенной нагрузки p (см. рис.1).
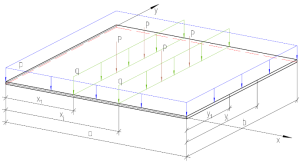
Рис. 1. Пластина под действием различных нагрузок
Согласно [1], используя разрывные импульсные функции, нагрузку вдоль линии q запишем в виде:
где ![]() — единичная импульсная функция;
— единичная импульсная функция; ![]() — координата по x приложения нагрузки;
— координата по x приложения нагрузки;
сосредоточенную нагрузку P:
![]() .
.
Подставим данные выражения для нагрузок в уравнение прогиба для тонкой пластины:
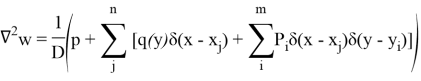
Решение уравнения будем искать методом Власова-Канторовича, сводя краевую задачу для уравнения в частных производных к решению обыкновенных дифференциальных уравнений.
Представим искомую функцию прогиба w тригонометрическим рядом:
![]() ,
, ![]() ,
,
решение будет представлять из себя систему из k обычных дифференциальных уравнений.
Функции нагрузок примут вид:
по линии
![]() ,
, ![]() ,
,
сосредоточенные
![]() ,
,
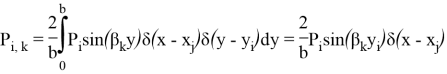
распределенная
![]() ,
, ![]() .
.
Преобразуем уравнение прогиба, которое теперь зависит от одной переменной:
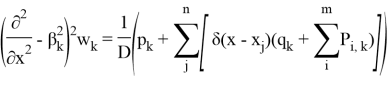
Решение уравнения согласно [1] можно представить в виде:
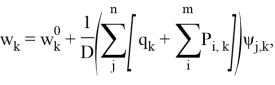
где
![]() — решение для
— решение для ![]() .
.
![]() ,
,
![]() ,
,
где ![]() единичная ступенчатая функция;
единичная ступенчатая функция; ![]() — постоянные интегрирования, определяются в зависимости от закрепления пластины.
— постоянные интегрирования, определяются в зависимости от закрепления пластины.
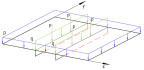
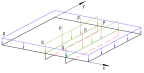
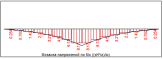
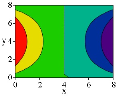
При рассмотрении пластин, усиленных ребрами жесткости, параллельных одной из осей (см. рис. 2), учет ребер так же можно выполнить с помощью дельта-функции.
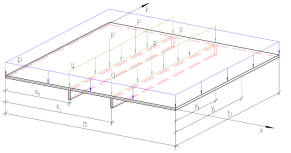
Рис. 2. Пластина, подкрепленная ребрами жесткости
Выразим согласно [3] продольные усилия и моменты, возникающие в ребристой пластине. Сопротивлением ребер кручению можно пренебречь ввиду малой жесткости на кручение в сравнении с изгибной.
![]() ,
,
![]() ,
,
где
Составим уравнения равновесия:
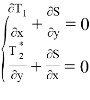 ,
, ![]() .
.
Перейдем к уравнениям относительно функций перемещения и преобразуем первые два уравнения согласно [2]:
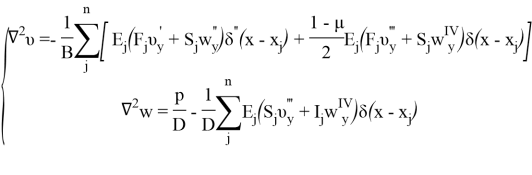
Если пренебречь влиянием ребер на продольные и сдвигающие усилия, то вместо системы получим уравнение относительно прогиба, что существенно упрощает задачу при незначительном уменьшении точности.
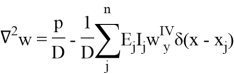
Ниже, при проведении сравнений результатов на конкретных примерах, рассматриваются оба варианта расчета: с учетом и без учета продольных усилий.
Согласно [1], дифференциальные уравнения с импульсными коэффициентами
![]() ,
,
(в уравнениях здесь и ниже индекс k опущен)
где
![]() — дифференциальный оператор, имеющий порядок не выше порядка оператора
— дифференциальный оператор, имеющий порядок не выше порядка оператора ![]() ,
,
имеют решение в виде:
![]() ,
,
где ![]() есть решение уравнения
есть решение уравнения ![]() ;
;
![]() — решение уравнения
— решение уравнения ![]() ;
;
![]() — коэффициент пропорциональности для решения уравнения, и находящийся из системы
— коэффициент пропорциональности для решения уравнения, и находящийся из системы
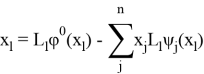
где в рамках рассматриваемой задачи обретает физический смысл, как прогиб пластины при ![]() . Без учета продольных усилий
. Без учета продольных усилий
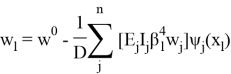
C учетом продольных усилий, решение системы уравнений приводим согласно [2]:
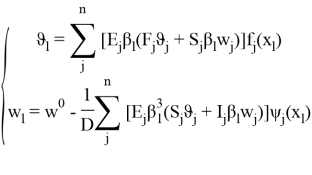
где, ![]()
При приложении распределенной, сосредоточенных и распределенных по линиям ребер нагрузок получаем систему уравнений:
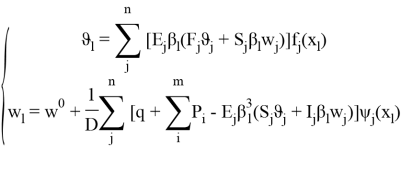
Порядок данной системы уравнений 2n. Для нахождения прогиба по формуле ![]() , при использовании трех членов ряда (при k=1, 3, 5) достаточно решить три независимых системы порядка 2n, что позволяет решить задачу без особого труда стандартными офисными программами, такими как Excel. В данной работе для проверки решений и анализа результатов использовалась система Mathcad, был разработан алгоритм и приведены результаты расчетов.
, при использовании трех членов ряда (при k=1, 3, 5) достаточно решить три независимых системы порядка 2n, что позволяет решить задачу без особого труда стандартными офисными программами, такими как Excel. В данной работе для проверки решений и анализа результатов использовалась система Mathcad, был разработан алгоритм и приведены результаты расчетов.
В таблице 1 приведены результаты расчетов прогибов для различных схем загружения пластины в сравнении с МКЭ.
Таблица 1
|
Схема нагружения |
x, м |
y, м |
Учитываемые нагрузки |
Аналитическое решение |
МКЭ |
|(wМКЭ- wан)/ wМКЭ|100,% |
Примечание |
|
|
|
|
|||||||
|
|
|
4 |
4 |
P |
4.05 |
4.14 |
2.2 |
Сетка МКЭ 1 х 1 м |
|
4 |
4 |
4.09 |
1.0 |
0.5 х 0.5 м |
||||
|
4 |
4 |
4.08 |
0.7 |
0.25 х 0.25 м |
||||
|
4 |
4 |
4.07 |
0.5 |
0.1 х 0.1 м |
||||
|
4 |
4 |
Q |
6.31 |
6.34 |
0.5 |
0.5 х 0.5 м |
||
|
4 |
4 |
P |
32.8 |
33.6 |
2.4 |
0.5 х 0.5 м |
||
|
4 |
4 |
p+P |
36.75 |
37.7 |
2.5 |
- //- |
||
|
4 |
4 |
p+q |
39.01 |
39.9 |
2.2 |
|||
|
4 |
4 |
p+P+q |
43.06 |
43.99 |
2.1 |
|||
|
|
|
4 |
4 |
P |
3.06 |
3.02 |
1.3 |
Без учета продольных усилий |
|
4 |
4 |
3.00 |
0.7 |
с учетом продольных усилий |
||||
|
4 |
4 |
Q |
3.05 |
2.96 |
3.0 |
- //- |
||
|
4 |
4 |
2.99 |
1.0 |
- //- |
||||
|
4 |
4 |
P |
8.00 |
7.81 |
2.4 |
|||
|
4 |
4 |
7.85 |
0.5 |
|||||
|
3 |
4 |
8.14 |
8.17 |
0.4 |
||||
|
3 |
4 |
8.00 |
2.1 |
|||||
|
4 |
4 |
p+P |
11.05 |
10.83 |
2.0 |
|||
|
4 |
4 |
10.84 |
0.1 |
|||||
|
3 |
4 |
10.85 |
10.83 |
0.2 |
||||
|
3 |
4 |
10.66 |
1.6 |
|||||
|
4 |
4 |
p+q |
11.04 |
10.78 |
2.4 |
|||
|
4 |
4 |
10.83 |
0.5 |
|||||
|
3 |
4 |
10.86 |
10.8 |
0.6 |
||||
|
3 |
4 |
10.67 |
1.2 |
|||||
|
4 |
4 |
p+P+q |
14.1 |
13.8 |
2.2 |
|||
|
4 |
4 |
13.83 |
0.2 |
|||||
|
3 |
4 |
13.57 |
13.47 |
0.7 |
||||
|
3 |
4 |
13.33 |
1.0 |
|||||
|
|
|
3 |
4 |
P |
5.48 |
5.36 |
2.2 |
|
|
3 |
4 |
5.40 |
0.8 |
|||||
|
4 |
4 |
5.95 |
5.72 |
4.0 |
||||
|
4 |
4 |
5.86 |
0.2 |
|||||
|
3 |
4 |
Q |
3.36 |
3.25 |
3.4 |
|||
|
3 |
4 |
3.31 |
1.8 |
|||||
|
4 |
4 |
3.64 |
3.51 |
3.7 |
||||
|
4 |
4 |
3.59 |
2.3 |
|||||
|
3 |
4 |
P |
6.76 |
6.63 |
2.0 |
|||
|
3 |
4 |
6.58 |
0.8 |
|||||
|
4 |
4 |
6.99 |
6.81 |
2.6 |
||||
|
4 |
4 |
6.8 |
0.1 |
|||||
|
3 |
4 |
p+P+q |
15.63 |
15.18 |
3.0 |
|||
|
3 |
4 |
15.41 |
1.5 |
|||||
|
4 |
4 |
16.58 |
16.1 |
3.0 |
||||
|
4 |
4 |
16.34 |
1.5 |
|||||
|
|
|
3.5 |
4 |
p+P+q |
17.4 |
17.5 |
0.6 |
|
|
3.5 |
4 |
17.9 |
2.3 |
|||||
|
4 |
4 |
17.2 |
17.1 |
0.6 |
||||
|
4 |
4 |
17.66 |
3.3 |
|||||
|
6 |
4 |
12.7 |
12.7 |
0.0 |
||||
|
6 |
4 |
13.1 |
3.1 |
|||||
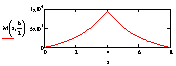
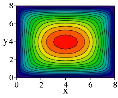
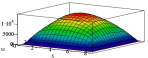
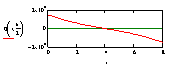
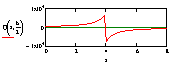
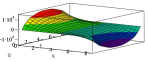
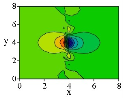
Ниже представлены графики моментов и перерезающих сил, определенных для различных загружений пластины, аналитически при удержании четырех членов ряда в сравнении с МКЭ.
Параметры пластины для таблицы 2: ![]()
![]() ,
, ![]() .
.
Таблица 2
|
Пластина под действием распределенной нагрузки
|
Пластина под действием сосредоточенной нагрузки
|
Пластина под действием нагрузки по линии
|
|
|
Mx (x, b/2) Аналити-чески |
|
|
|
|
|
|
|
|
|
Mx (x, b/2) МКЭ |
|
|
|
|
Mx (x, b/2) Наложение результатов по двум методикам |
|
|
|
|
Qx (x, b/2) Аналити-чески |
|
|
|
|
|
|
|
|
|
Qx (x, b/2) МКЭ |
|
|
|
|
Qx (x, b/2) Наложение результатов по двум методикам |
|
|
|
Из таблицы видно, что даже при использовании трех членов ряда, результаты расчетов, полученные описанным выше методом, коррелируют с результатами, полученными МКЭ. При этом при сетке разбивки МКЭ 0.5х0.5 м разница с аналитическим методом составляет не более 4 %. При сгущении сетки решение приближается к аналитическому.
По графикам, представленным в таблице 2, для сосредоточенных нагрузок виден характер распределения производных разрывных функций. Эти графики в точке
Результаты вычислений показывают, что в сравнении с МКЭ при определении напряженно-деформированного состояния вблизи приложения сосредоточенных нагрузок с удержанием малого числа членов ряда, благодаря наличию разрывных функций компоненты НДС определяются в зоне разрыва с такой же точностью, как и в зоне плавного изменения нагрузки. Для улучшения результатов в МКЭ необходимо сгущать сетку разбивки, что приводит к значительному повышению порядка системы разрешающих уравнений.
Литература:
- Михайлов Б. К. Пластины и оболочки с разрывными параметрами. — Л.: ЛГУ, 1980. — 196 с.
- Кобелев Е. А. Изгиб пластин, соединенных системой перекрестных ребер // Строительная механика сооружений: Межвуз. темат. Сб. тр. / ЛИСИ. — Л., 1986. — С. 99–104.
- Гребень Е. С. Основные соотношения технической теории ребристых оболочек. // Изв. АН СССР. Механика. — 1965. — № 3. — С. 81–92.
- Кобелев Е. А. Изгиб пластин с разрезами и прямоугольными отверстиями, подкрепленными ребрами: Дис…канд. Техн. наук. — Л.: ЛИСИ, 1984. — 208 с.
- Фирсанов В. В. Исследование продольно подкрепленных цилиндрических оболочек под действием локальной нагрузки по уточненной теории / В.В Фирсанов, А. Х. Во // Труды МАИ. — 2018. — № 102.
- Петров В. В. Расчет конструкций переменной толщины методом наискорейшего спуска / В. В. Петров, Д. А. Пименов, Р. В. Мищенко // Научный журнал «ACADEMIA. АРХИТЕКТУРА И СТРОИТЕЛЬСТВО». — 2018. — № 2. — С. 137–142.
- Зверяев Е. М., Макаров Г. И. Особенности НДС оболочки с изломом срединной поверхности / Е. М. Зверяев, Г. И. Макаров // Строительная механика и расчет сооружений. — 2013. — № 3. — С. 2–6.
- Таскин И. А. Распределение усилий между рёбрами и настилом в пологом сетчатом куполе / И. А. Таскин // Строительная механика и расчет сооружений. — 2016. — № 3. — С. 110–115.
- Соловей Н. А., Кривенко О. П., Малыгина О. А. Конечноэлементные модели исследования нелинейного деформирования оболочек ступенчато-переменной толщины с отверстиями, каналами и выемками / Н. А. Соловей, О. П. Кривенко, О. А. Малыгина // Magazine of Civil Engineering. — 2015. — № 1. — С. 52–109.
- Семенов А. А., Панин А. Н. Эффективность использования безразмерных параметров при расчете прочности и устойчивости подкрепленных пологих оболочек / А. А. Семенов, А. Н. Панин // Академический вестник УРАЛНИИПРОЕКТ РААСН. — 2015. — № 3. — С. 73–76.
- Карпов В. В. Напряженно-деформированное состояние ребристых оболочечных конструкций / В. В. Карпов, О. В. Игнатьев, А. А. Семенов // Инженерно-строительный журнал. — 2017. — № 6(74). — С. 147–160.