Гидравлическое сопротивление является одной из важных физических величин, характеризующих фильтрацию жидкости в пористой среде. В данной статье делается попытка определения гидравлического сопротивления при фильтрации жидкости в зонально неоднородном пласте.
Ключевые слова: гидравлическое сопротивление, зональная неоднородность, фильтрация жидкости, число Рейнольдса, среднее значение.
Предположим, что фильтрация в пласте происходит по закону Дарси. Тогда скорость фильтрации можно определить по формуле [1,2]:
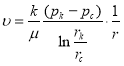 (1)
(1)
Определим гидравлическое сопротивление, которое образуется при такой фильтрации жидкости:
![]() где
где ![]() (2)
(2)
тогда
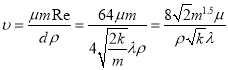 (3)
(3)
А теперь предположим, что имеется зонально-неоднородный пласт, состоящий из двух зон. Первая имеет протяженность от ![]() до
до ![]() , а вторая от
, а вторая от ![]() до
до ![]() .
.
Учитывая (1), (3) и приравнивая правые части формул, получим следующие выражения:
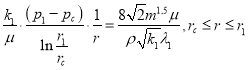 (4)
(4)
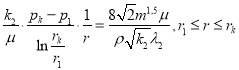 (5)
(5)
или 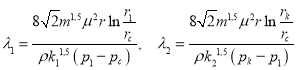 (6)
(6)
Представим уравнения (4) и (5) в виде:
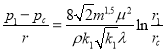 (7)
(7)
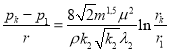 (8)
(8)
Если сложим по отдельности правые и левые части этих уравнений, то получим:
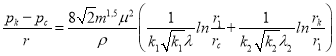 (9)
(9)
Среднее значение проницаемости и гидравлического сопротивления можно определить из равенства скоростей в реальном неоднородном и эквивалентно однородном пластах:
Для эквивалентного однородного пласта:
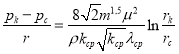 (10)
(10)
Приравнивая правые части формул (8) и (9) и произведя несложные преобразования получаем:
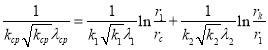 (11)
(11)
С другой стороны, дебит потока в силу установившегося движения несжимаемой жидкости будет постоянен через любую цилиндрическую поверхность, соосную скважине:
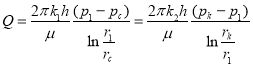 (12)
(12)
Используя свойство производных пропорций, находим из последних равенств:
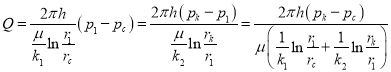 (13)
(13)
Здесь также среднее значение проницаемости можно определить из равенства дебитов аналогичных потоков в неоднородном и однородном пластах:
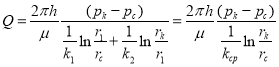 (14)
(14)
откуда имеем
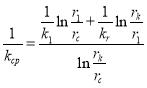 или
или 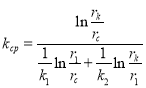 (15)
(15)
При наличии в пласте двух кольцевых зон с различной проницаемостью распределение давления в этих зонах можно найти, приравнивая скорости на границе этих зон, т. е.
при
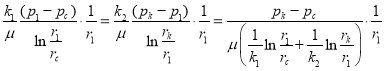 (16)
(16)
Здесь также использовано свойство производных пропорций, тогда:
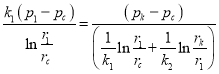
или 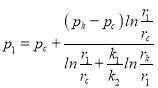 (17)
(17)
Подставляя значение ![]() из (17) в формулах (6) получаем
из (17) в формулах (6) получаем
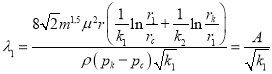 (18)
(18)
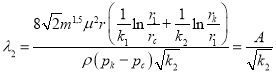 (19)
(19)
где 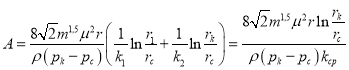 (20)
(20)
Здесь использована формула (15) для ![]() .
.
Так как аналогично формулам (6)
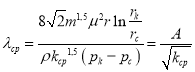 (21)
(21)
А теперь выразим ![]() через
через ![]() и
и ![]() . Для этого используем формулу (15). Умножая правую и левую части уравнения (15) на
. Для этого используем формулу (15). Умножая правую и левую части уравнения (15) на ![]() получаем:
получаем:
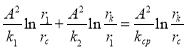 (22)
(22)
Учитывая (18), (19) и (21) имеем
![]() (23)
(23)
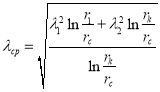 (24)
(24)
Последнюю формулу можно также получить, умножая обе части формулы (11) на ![]() .
.
Обобщив формулу (24) можно сказать, что если неоднородный пласт состоит из ![]() зон то, для каждой зоны гидравлические сопротивления будут соответственно
зон то, для каждой зоны гидравлические сопротивления будут соответственно
![]() (25)
(25)
где А определяется с помощью формулы (20).
А среднее значение гидравлического сопротивления эквивалентного однородному пласту можно определить с помощью формулы
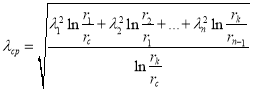 (26)
(26)
Таким образом, в данной статье получены формулы для определения гидравлических сопротивлений, каждой зоны. А также дается формула для среднего значения гидравлического сопротивления эквивалентного однородному пласту.
Литература:
- Подземная гидравлика. Учебник для вузов./ К. С. Басниев, А. М. Власов, И. Н. Кочина, В. М. Максимов.-М.:Недра, 1986–303 с.
- Чарный И. А. Подземная гидрогазодинамика. М.: Гостоптехиздат, 1963.







