В статье исследуется немодельное двумерное интегральное уравнение типа Вольтерра с слабо-особой и сильно-особой линией на полосе. В случае, когда функции, присутствующие в ядрах, не связаны между собой, решение немодельного двумерного интегрального уравнения типа Вольтерра с особой и слабо-особой линией сводится к решению двумерного интегрального уравнения со слабой особенностью на полосе. Решение интегрального уравнения выражается через резольвенту интегрального уравнения со слабой особенностью.
Ключевые слова: немодельное интегральное уравнение, сильно-особая линия, слабая особенность, резольвента.
In this article investigates a non-model two-dimensional Volterra-type integral equation with a weakly-singular and a strongly-singular line on the band. In the case where the functions present in the nuclei are unrelated, the solution of a non-model two-dimensional Volterra-type integral equation with a singular and weakly singular line is reduced to the solution of a two-dimensional integral equation with a weak singularity on the band. The solution of the integral equation is expressed in terms of the resolvent of the integral equation with a weak singularity.
Key words: non-model integral equation, strong-singular line, weak singularity, resolvent.
Через D обозначим область ![]() . Границы области соответственно обозначим:
. Границы области соответственно обозначим: ![]()
![]() В области D рассмотрим двумерное интегральное уравнение вида:
В области D рассмотрим двумерное интегральное уравнение вида:
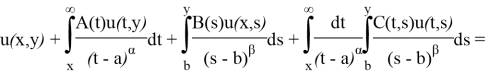
где ![]()
![]()
![]() заданные функции соответственно на
заданные функции соответственно на ![]() и
и ![]()
![]() искомая функция,
искомая функция, ![]() .
.
Интегральное уравнение (1) будем исследовать при предположении, что ![]()
Решение интегрального уравнения (1) будем искать в классе функций
![]() с асимптотическим поведением
с асимптотическим поведением
![]() ,
,
![]() с асимптотическим поведением
с асимптотическим поведением
![]() .
.
В [1] изучено немодельное двумерное интегральное уравнение типа Вольтерра с граничным слабо-сингулярным ядром в случае, когда функции присутствующие в ядрах связаны и не связаны между собой в первом квадранте.
Работы [2], [3], [4] посвящены изучению модельного двухмерного интегрального уравнения типа Вольтерра с особой и слабо-особой линией на полосе в случае, когда параметры уравнения связаны между собой и не связаны между собой, работа [5] посвящена постановке граничных задач и их решению модельных двумерных интегральных уравнений типа Вольтерра с особой и слабо-особой линией на полосе.
Допустим, что в уравнении (1) ![]() В этом случае, согласно [1] уравнение (1) представим виде:
В этом случае, согласно [1] уравнение (1) представим виде:
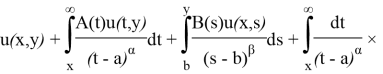
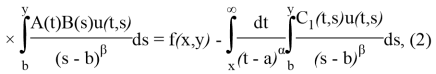
где
![]()
По обе стороны (2) действуя при помощи интегрального оператора ![]() , после слагаемое, которое содержит неизвестную функцию
, после слагаемое, которое содержит неизвестную функцию ![]() перенося в левую часть, приходим к решению интегрального уравнения:
перенося в левую часть, приходим к решению интегрального уравнения:
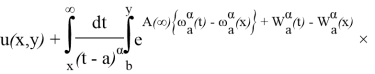
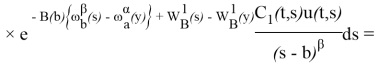
![]() (3)
(3)
где
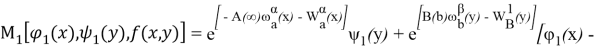
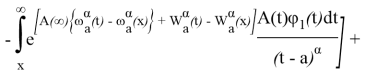
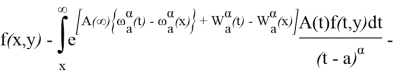
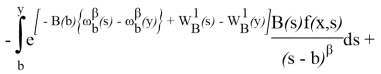
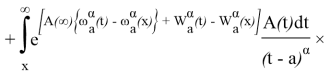
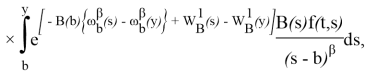
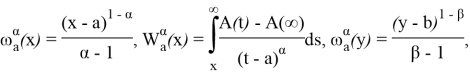
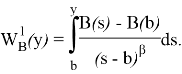
Далее, при![]()
![]() вводя обозначение
вводя обозначение
![]()
уравнение (3) представим в виде
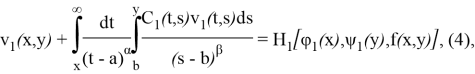
где
![]()
Справедливы следующие утверждения:
Теорема 1. Пусть в интегральном уравнении (1) ![]() ,
, ![]() ,
, ![]()
![]() и в окрестности точек
и в окрестности точек ![]()
![]() удовлетворяют условиям:
удовлетворяют условиям:
![]()
![]()
![]() (5)
(5)
![]() при
при ![]() (6)
(6)
![]()
![]() ,
, ![]()
![]() и на
и на ![]() и
и ![]() обращается в нуль с асимптотическими поведениями
обращается в нуль с асимптотическими поведениями
![]()
![]() при
при ![]() (7)
(7)
![]() при
при ![]() (8)
(8)
Функция ![]() и на
и на ![]() и
и ![]() обращается в нуль с асимптотическими поведениями
обращается в нуль с асимптотическими поведениями
![]()
![]() при
при ![]()
Тогда задача о нахождении интегрального уравнения (1) в классе функций ![]() обращающеется в нуль на
обращающеется в нуль на ![]() и
и ![]() эквивалентна задаче о нахождении решения двумерного интегрального уравнения типа Вольтерра со слабой особенностью (4).
эквивалентна задаче о нахождении решения двумерного интегрального уравнения типа Вольтерра со слабой особенностью (4).
Теорема 2. Пусть в интегральном уравнении (1), ![]() функции
функции ![]()
![]() и в окрестности точек
и в окрестности точек ![]()
![]() соответственно удовлетворяют условиям (5), (6),
соответственно удовлетворяют условиям (5), (6), ![]()
![]() на
на ![]() и
и ![]() обращается в нуль с асимптотическими поведениями
обращается в нуль с асимптотическими поведениями
![]()
![]() при
при ![]()
![]() при
при ![]()
Функция![]() и на
и на ![]() и
и ![]() обращается в нуль с асимптотическими поведениями (7), (8). Тогда интегральное уравнение (1) имеет единственное решение, которое выражается равенством:
обращается в нуль с асимптотическими поведениями (7), (8). Тогда интегральное уравнение (1) имеет единственное решение, которое выражается равенством:
![]()
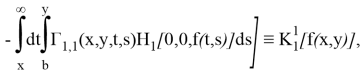
где ![]()
![]() резольвента двумерного интегрального уравнения со слабой особенностью (4).
резольвента двумерного интегрального уравнения со слабой особенностью (4).
Литература:
-
Раджабова Л. Н., Раджабов Н. К теории одного класса двумерного слабо-сингулярного интегрального уравнения типа Вольтерра на первом квадранте// Доклады Академии Наук Республики Таджикистан
 2014.
2014. Т. 57. № 6.
Т. 57. № 6.  С. 443–451.
С. 443–451.
- Раджабова Л. Н., Хушвахтов М. Б. К теории особых двумерных интегральных уравнений типа Вольтерра с особой и слабо-особой линией на полосе// Вестник Таджикского национального университета. Серия естественных наук. — 2017. — № 1/3. — С.3–5.
- Раджабова Л. Н., Хушвахтов М. Б. К теории особых двумерных интегральных уравнений типа Вольтерра с особой и слабо-особой линией на полосе в случае, когда параметры уравнения не связаны между собой// Доклады Академии Наук Республики Таджикистан. — 2018. — Т. 61. № 4. — С. 331–337.
- Хушвахтов М. Б. О некоторых случаях двумерных интегральных уравнений типа Вольтерра с особой и слабо-особой линией на полосе// Вестник Таджикского национального университета. Серия естественных наук. — 2019. — № 1. — С.44–49.
- Хушвахтов М. Б. Граничные задачи для двумерных интегральных уравнений типа Вольтерра с сильно-особой и слабо-особой линией на полосе. Материалы республиканской научной конференции, посвящённой 80-летию видного таджикского математика, профессора Бекназара Имомназарова (Таджикистан, г.Душанбе, 10–11 июня 2019г.). –Душанбе:2019.– С.263–267.







