Рассматривается задача влияния выбора соотношения размеров конструктивных элементов движителей шагающих роботов на энергоэффективность мобильного робота.
Ключевые слова: движитель, мобильный робот, энергоэффективность.
Введение
Устройство, технические характеристики и возможности шагающей машины во многом определяются типом движителей, которыми оснастили её разработчики. Наиболее распространенные схемы шагающих движителей: пантографная, ортогональная, инсектоморфная, телескопическая, человекоподобная. Выбор типа механизма шагания из известных [1,2] во многом предопределяется предназначением машины и типом местности, по которой ей предстоит передвигаться, а также допустимыми габаритами робота. Значительными габаритами отличаются ортогональные и пантографные механизмы [3]. Больше мобильности в ограниченном пространстве при тех же размерах основания машины позволят получить телескопическая, лошадиная или человекоподобная схемы движителей. Значительным фактором выбора схемы движителей для мобильного робота должна быть его энергетическая эффективность. Современный уровень развития методов сохранения электрической энергии не позволяет разработчику мобильного робота не экономить на затратах энергии для движения машины в пользу длительности работы.
Постановка задачи
Энергетическая эффективность шагающей машины известная проблема [4,5,6] имеющая ряд решений связанных, как с подбором оптимальной программы управления движением робота, выбором более производительных двигателей и. т.д. Также свой вклад в общую энергоэффективность машины может внести подбор конструктивных размеров конкретных элементов конструкции шагающего движителя исходя не только из размеров машины и препятствий, которые ей предстоит преодолеть, но и из наименьших затрат на перемещение робота.
Максимального уровня энергетической эффективности для шагающих движителей человекоподобной и телескопической схем можно добиться подобрав оптимальные геометрические характеристики длин частей движителей, а также углов взаимного их расположения.
Для человекоподобной схемы:
![]() (1)
(1)
Для телескопической схемы:
Где М — моменты в «суставах» движителей, a,b — коэффициенты, зависящие от типа используемых двигателей. ![]() - время, шага движителя за которое он проходит заданное расстояние S c некоторой скоростью V.
- время, шага движителя за которое он проходит заданное расстояние S c некоторой скоростью V.
Метод решения
Составляются уравнения равновесия для движителя каждого типа.
Для человекоподобной схемы, по кинематической схеме на рисунке 1.
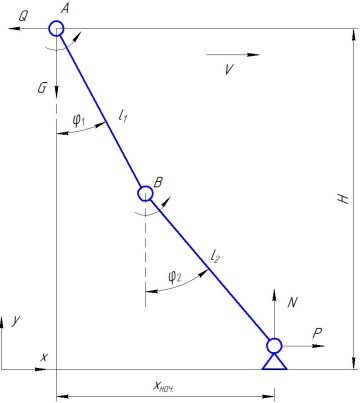
Рис. 1. Кинематическая схема человекоподобного механизма шагания: φ1, φ2 — углы взаимного расположения секций механизма; l1, l2 — длины секций механизма; H- клиренс механизма
Уравнения равновесия выглядят следующим образом:
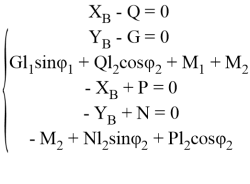 (3)
(3)
Решение системы уравнений позволяет получить значения моментов М1 и М2 в «суставах» движителя, необходимых для определения энергетической эффективности шагающего движителя при заданных геометрических параметрах. Находить решение системы уравнений (3), необходимо выполняя следующие условия:
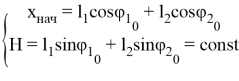 (4)
(4)
Для телескопической схемы уравнения равновесия составляются по кинематической схеме на рисунке 2.
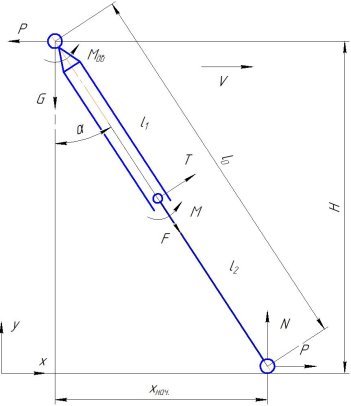
Рис. 2. Кинематическая схема телескопического механизма шагания: α — угол наклона движителя; l0 — начальная длина движителя; l1, l2 — длины секций механизма; H- клиренс механизма
Уравнения равновесия для телескопической схемы механизма шагания выглядят следующим образом:
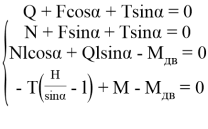 (5)
(5)
Где F=M*ρ
Решение системы уравнений позволяет получить значения моментов М и Мдв в «суставах» движителя, необходимых для определения энергетической эффективности шагающего движителя при заданных геометрических параметрах. Находить решение системы уравнений (5), необходимо выполняя следующие условия:
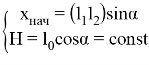 (6)
(6)
Результаты
Совместное решение систем уравнений 3 и 4 при заданных, как начальные условия H, l1, l2 и получение показателя энергоэффективности (1) для человекоподобного движителя дает возможность разработчику оценить и выбрать наиболее эффективные параметры для построения мобильного робота с данным типом движителя. Уравнения решаются не для одного набора значений углов φ1 и φ2 и позволяют получить широкий массив данных, примеры графиков значений φ1 и φ2 приведены на рисунках 3 и 4.
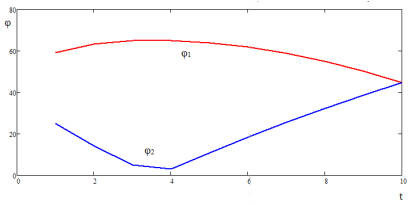
Рис. 3
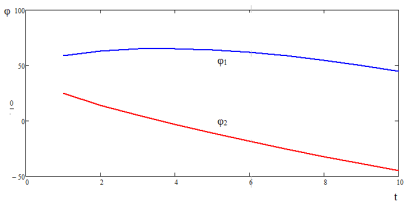
Рис. 4
Совместное решение систем уравнений 5 и 6 при заданных, как начальные условия H, l1, l2 и получение показателя энергоэффективности (2) для телескопического движителя дает массив данных для оценки наиболее эффективных параметров мобильного робота с данным типом движителя. Уравнения также, как и в случае человекоподобного движителя решаются для нескольких значений угла α, примеры графиков значений α и l2 приведены на рисунках 5 и 6.
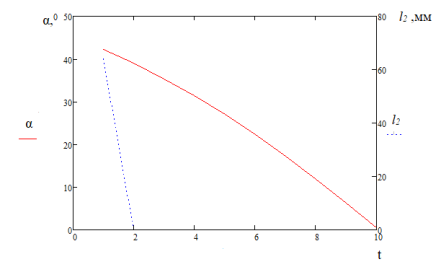
Рис. 5
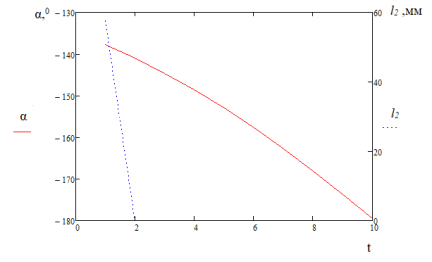
Рис. 6
Выводы
Вычисление энергетической эффективности описанным методом упрощает разработку мобильных роботов, позволит сэкономить средства на изготовление опытных образцов механизмов с заведомо низкими показателями. Автоматизация процесса вычислений приведенным методом позволит разработчику подбирать наилучшие варианты конструкции мобильного робота с точки зрения энергетической эффективности, а также сравнивать различные схемы шагающих движителей между собой.
Литература:
- Mathematical modelling of mobile robot motion with propulsion device of discrete interacting with the support surface / Briskin E. S., Kalinin Y. V., Maloletov A. V.,Sharonov N. G. / IFAC-PapersOnLine (см. в книгах). 2018. Т. 51. № 2. С. 236–241.
- Шагающая опора для транспортных средств повышенной проходимости / Охоцимский Д. Е., Брискин Е. С., Чернышев В. В., Шерстобитов С. В. / патент на изобретение RUS 2156711 09.06.1999
- Динамика и управление движением шагающих машин с цикловыми движителями Брискин / Е.С., Жога В. В., Чернышев В. В., Малолетов А. В./ Машиностроение. 2009. С.12–15.
- Об управлении движением автономного робототехнического комплекса с якорно-тросовым движителем / Платонов В. Н., Брискин Е. С., Шаронов Н. Г. / В книге: Прогресс транспортных средств и систем — 2018 Материалы международной научно-практической конференции. Под редакцией И. А. Каляева, Ф. Л. Черноусько, В. М. Приходько. 2018. С. 146–148.
- Оптимизация в инженерных и управленческих задачах / Волчков В. М., Годенко А. Е., Калинин Я. В., Тарасова И. А. / Учеб. пособие / Волгоград, 2018.
- Математическое моделирование робота с переменным вектором тяги / Павловский В. Е., Яцун С. Ф., Емельянова О. В., Стуканёва С. П. / В сборнике: Второй Всероссийский научно-практический семинар «Беспилотные транспортные средства с элементами искусственного интеллекта» Труды семинара. Российская ассоциация искусственного интеллекта. 2015. С. 99–106.







