Статья посвящена методике работы с динамическими графиками гармонических колебаний при показе. В статье подробно описан способ работы с данным графиком.
Ключевые слова: график, «Microsoft Excel» 2010, полоса прокрутки, динамический график, гармонические колебания.
Графическое представление информации всё шире и шире используется в современном мире, поэтому умения извлекать сведения из графиков, диаграмм и таблиц необходимы как будущему учителю, так и вообще образованному человеку. Обычные статические графики, конечно, прививают некоторые необходимые навыки, но динамические позволяют делать это более наглядно и полно. [1, с.122]
В школьном курсе «Физика 9 класс» при изучении раздела «Механика» рассматриваются такие виды графиков как синусоида, прямая и др. При работе с графиками учителя могут сталкиваться с проблемой понимания учащимися влияния параметров периода и амплитуды на общий вид графика гармонических колебаний или научить учащихся извлекать из него необходимые данные. [2, с.98]
Для более быстрого понимания учениками графика и облегчения работы учителя можно использовать динамические графики. Прежде чем начать работать с графиком, стоит познакомиться с указаниями к работе с динамическими графиками, приведёнными ниже.
- При работе с файлом нельзя удалять и изменять столбцы и строки, т. к. в них содержатся данные, при исчезновении которых график не будет выполнять своей функции.
- Если необходимо, чтобы столбцы с данными не отображались, следует воспользоваться командой «Масштаб», которая находится в правом нижнем углу, нажимая на «+» происходит увеличение, при нажатии на «-» уменьшение листа, кроме этого, можно сдвинуть лист, воспользовавшись полосами прокрутки окна Excel.
- Также у каждой программы, в которой вы можете открыть данные графики, будь то Microsoft Exсel 3 или 10, существует своя специфика работ с полосой прокрутки.
В Microsoft Exсel 10 для изменения графика можно, например, использовать кнопки, которые находятся на концах полосы прокрутки, при щелчке на кнопку происходят изменения счётчика на 1 шаг. Также менять данные можно, перемещая бегунок, в этом случае график будет меняться только после того, как будет отпущена левая кнопка мыши.
При закрытии файла после работы ни в коем случае не следует сохранять изменения, даже если программа предлагает это сделать, так как может произойти сохранение разного рода ощибок.
Проверка алгоритма работы полосы прокрутки должна быть произведена до начала работы с графиком, так как в зависимости от используемой версии Microsoft Exсel алгоритм работы может быть разным.
На рисунке 1 представлен график гармонических колебаний.
График построен по функции
y=A*sin (ωt+0)
Параметры функции можно изменять при помощи трёх полос прокрутки
Амплитуду (А) от 0 до 50 см.
Период колебаний (Т) от 1 до 50 с.
Начальную фазу (0) от (–π/2) до (+π/2)
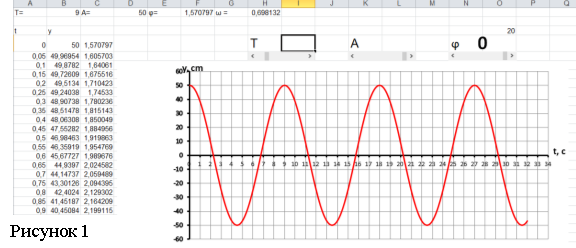
Эти возможности позволяют продемонстрировать практически все особенности гармонических колебаний.
График гармонических колебаний представляет собой зависимость смещения от времени (
). Нами построен график гармонических колебаний с полосами прокрутки, с помощью которых можно изменять амплитуду, период и начальную фазу колебаний.
При изменении параметра амплитуды (А) от 0 до 50 см график будет вытягиваться или сжиматься вдоль оси y. Рассмотрим несколько примеров, где период колебаний (Т=6с) и начальная фаза (0 =1,57…) остаются неизменными, а параметр А будем менять при помощи полосы прокрутки. При демонстрации учителю стоит обратить внимание учащихся на изменение графика функции. Это можно сделать с помощью линии на графике или указки.
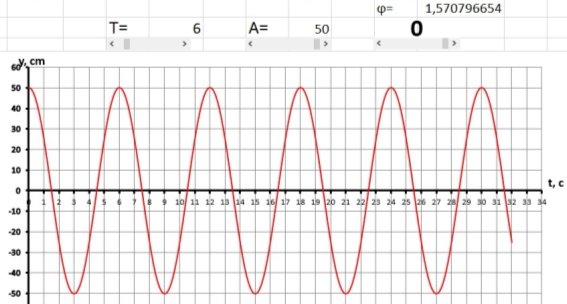
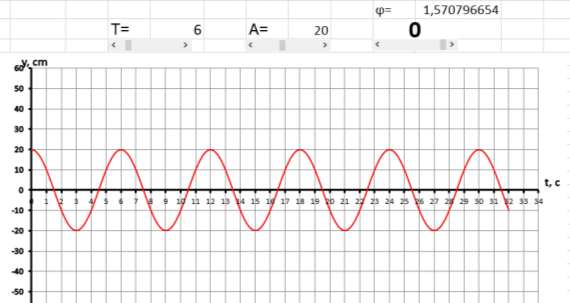
На рисунках 2а и 2б представлены графики, где амплитуда А= 50 см и А= 20см. Обращаем внимание учеников на то, как изменился график. Так как амплитуда — это максимальное отклонение от состояния равновесия на графике, она отображается как максимальное значение по оси y. Показываем, как изменилось значение амплитуды.
С помощью программы можно показать, как изменяется график функции при изменении периода колебаний (Т).
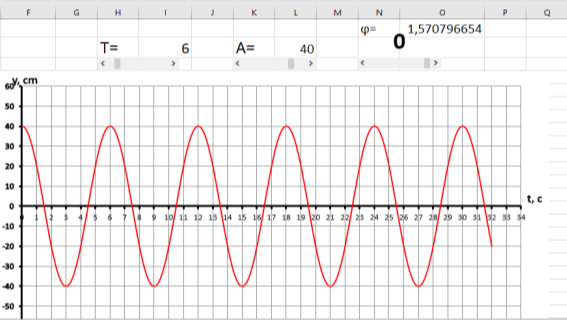
При изменении параметра период колебаний (Т) от 1 до 50 см график будет растягиваться или сжиматься вдоль оси t. Рассмотрим несколько примеров, где амплитуда (А=40см) и начальная фаза (0 =1,57…) остаются неизменными, а параметр Т меняется при помощи полосы прокрутки.
Обращаем внимание учеников на то, как изменился график. Так как период колебаний — это промежуток времени, в течение которого тело совершает одно полное колебание на графике, это можно отобразить как количество делений по оси t от одной вершины до другой. Показываем, как значение периода колебаний изменяется при Т=6см и Т=3 с. На рисунках 3а и 3б представлены графики того, как они должны выглядеть.
При помощи указки показываем момент времени, когда тело максимально отклонено. Первое максимальное отклонение t=0c, находим следующую точку, где тело максимально отклонено, это t=6c.
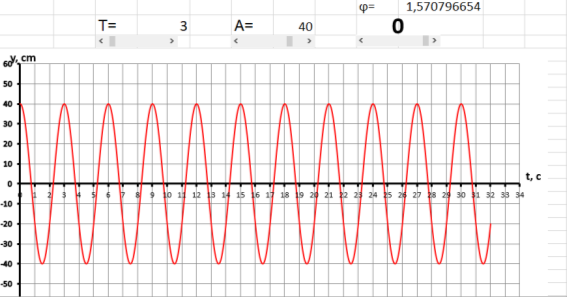
При изменении параметра начальной фазы (0) от (–π/2) до (+π/2) график будет смещаться вдоль оси t. Рассмотрим несколько примеров, где период колебаний (Т=3с) и амплитуда (А=40см) остаются неизменными, параметр начальной фазы (0) при этом будем менять с помощью полосы прокрутки. Учителю стоит обратить внимание учащихся на изменение графика функции. Это можно сделать с помощью указки.
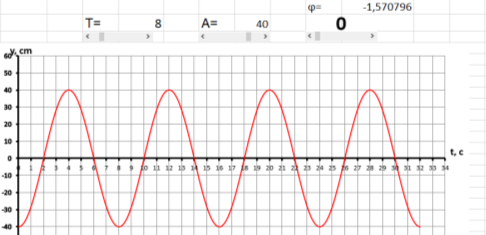
На рисунках 4а, 4б и 4в представлены графики, где начальная фаза 0= –π/2, 0= +π/2 и 0= 0. Обращаем внимание учеников на то, как изменился график. Так как начальная фаза — это значение фазы колебаний в начальный момент t=0 с. Показываем, как меняются значения при 0= –π/2, 0= +π/2 и 0= 0.
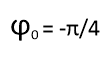
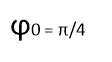
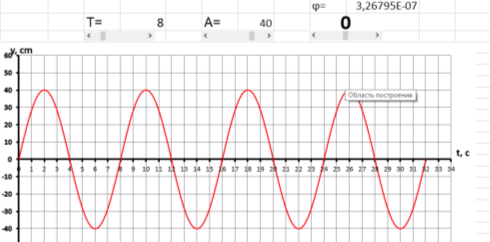
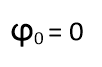
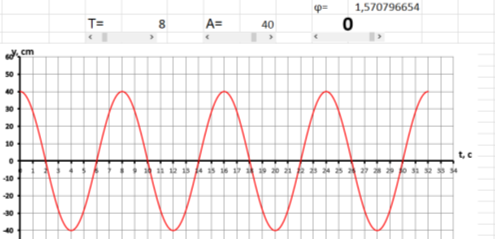
При сравнении графиков видно, что при отрицательной начальной фазе график сдвигается вправо, при положительной – влево.
При изучении гармонических колебаний, можно при помощи предлагаемой программы демонстрировать влияние амплитуды (А), периода колебаний (Т) и начальной фазу (0) на вид графика. Это поможет учащимся лучше понимать, что должно произойти при изменении того или иного параметра функции.
Литература:
- Бурлакова И. О. Правила построения графиков в пакете «Microsoft Excel» 2010/ Перспективные научные исследования: опыт, проблемы и перспективы развития. Сборник статей по материалам международной научно-практической конференции Ч-2. 2019
- Пёрышкин А. В. Физика 9 класс — М.: Дрофа, 2003. — 256 с.
